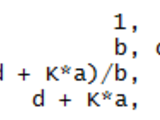Routh's array in symbolic way
[M L] = routh_hurwitz(P,N)
This function gives the Routh's array from a numerical or SYMBOLIC polynomial and includes two special cases: (1) the first element of the row is zero; (b) a row of zeros.
P Numerical or symbolic array of coeficients. In the case of symbolic variables it is necesarry to define them as: >> syms a b c ...
N Digits to be considered zero a number. E.g, for N=5, 10^(-5) is considered a zero. By default, N=10
M Routh's array without any simplification (e.g., with epsilon notation)
L Simplified first column of Routh's array with simplification (e.g., using the limit when epsilon tends to zero) that determines the number of roots in the right-half of the s-plane: the number of changes of signs in L
Examples:
1. [M, L]=routh_hurwitz([1 0 2 3 4])
2. syms a b c d K; [M, L]=routh_hurwitz([1 b c d+a*K])
3. syms k; [M, L]=routh_hurwitz([1 k 1 1])
4. [M, L]=routh_hurwitz([1 -3 -15 -9 -58 12 72])
5. syms a; [M, L]=routh_hurwitz([1 0 2 3 a])
Developed by Carlos M. Vélez S., cmvelez@eafit.edu.co
http://sistemascontrol.wordpress.com/
EAFIT University, http://www.eafit.edu.co
Medellín, Antioquia, Colombia
November 24th 2011
Cite As
Carlos M. Velez S. (2024). Routh's array in symbolic way (https://www.mathworks.com/matlabcentral/fileexchange/33926-routh-s-array-in-symbolic-way), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.