2-dimensional Filter Design using McClellan transformation
[Filter_1D,Filter_2D]=Filter_Design_2D_McClellan(Type,edges,Ap,Aa,transformation_vector)
This function can be used to design a lowpass, highpass, bandpass, or bandstop
two-dimensional filter which satisfies prescribed specifications.
_ Type can be "Lowpass", "Highpass", "Bandpass", or "Bandstop"
_ edges is a vector of normalized frequencies (rad/s) including passband and stopband edges.
(frequencies must be in an increasing order)
_ Ap: peak to peak passband ripple (db)
_ Aa: minimum stopband attenuation (db)
_ transformation_vector: this is a vector with 4 elements which maps 1D
space to 2D space [1]. These coefficients can be found based on the method
presented in [2]. Some examples are as follows:
2D Filter with circularly symmetric spectrum=[-0.5 0.5 0.5 0.5];
2D Filter with elliptic spectrum=[-2.4973 2.9006 0.3127 0.2840];
2D Filter with fan shape spectrum=[0 0.5 -0.5 0];
The algorithm first designs 1D filter based on kaiser method and
Dig_Filter(http://www.mathworks.com/matlabcentral/fileexchange/30321-digfilter).
Then by using the transformation vector and Chebyshev Polynomials
(http://www.mathworks.com/matlabcentral/fileexchange/4913-chebyshevpoly-m)
2D filter will be designed.
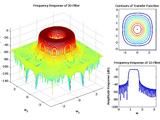
The amplitude response of 2D and 1D filters as well as contours of the
transformation function will be shown at the output.
[Filter_1D,Filter_2D] are 1D and 2D filters’ coefficients, respectively.
Example:
[Filter_1D,Filter_2D]=Filter_Design_2D_McClellan('lowpass',[0.1*pi,0.2*pi],0.5,30,[-0.5 0.5 0.5 0.5]);
Which designs a lowpass 2D FIR filter with circularly symmetric spectrum using Kaiser Method. Passband edge is 0.1*pi, and stopband edge is 0.2*pi,
Ap=0.5 (db) and Aa=30 (db).
https://www.youtube.com/watch?v=xYK4hcngt1g&feature=youtu.be
----------------------------------------
References:
[1] D.E. Dudgeon, R.M. Mersereau, "Multidimensional digital signal processing", Prentice-Hall.
[2] R.M. Mersereau, W.F.G.Mecklenbrauker, T.F. Quatieri, "McClellan transformations
for two-dimensional digital filtering: I-Design", IEEE transactions on circuit and systems, 1976.
To find other Matlab functions about filter design, please visit
http://www.ece.uvic.ca/~imanmoaz/index_files/index1.htm
Cite As
Iman (2024). 2-dimensional Filter Design using McClellan transformation (https://www.mathworks.com/matlabcentral/fileexchange/35051-2-dimensional-filter-design-using-mcclellan-transformation), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Signal Processing > Signal Processing Toolbox > Digital and Analog Filters > Digital Filter Design > FIR Filter Design >
Tags
Acknowledgements
Inspired by: ChebyshevPoly.m, Dig_Filter
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.