Convert Keplerian Orbital Elements to a State Vector

Convert orbital elements to a state vector, or a state vector back to orbital elements.

Most readily available Keplerian orbital element conversion utilities do not address circular or parabolic orbits. This set of routines will address the complete spectrum of orbits from a circular equatorial orbit to a retrograde hyperbolic orbit without error. All functionality is vectorized for computational efficiency.

Example Function Call One:
>> [r_ECI v_ECEF] = orb2rv(p,e,i,O,o,nu);

Where:
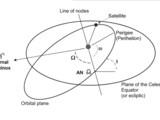
p = semilatus rectum (km) [1 x N]
e = Eccentricity [1 x N]
i = Inclination (rad) [1 x N]
O = Right Ascension of the Ascending Node (rad) [1 x N]
o = Argument of Perigee (rad) [1 x N]
nu = True Anomaly (rad) [1 x N]

Example Function Call Two:
>>[a,e,i,O,o,nu] = rv2orb(r_ECI,v_ECI)

Where
r = Position State Vector in km (ECI) [3 x N]
v = Velocity State Vector in km/s (ECI) [3 x N]

For those orbits which are equatorial or circular, the following full form function calls are necessary:

Convert state vector to full set of orbital elements:
>>[a,e,i,O,o,nu,truLon,argLat,lonPer,p] = rv2orb(r_ECI,v_ECI);

Convert full set of orbital elements back to a state vector:
>>[r_ECI,v_ECI] = orb2rv(p,e,i,O,o,nu,truLon,argLat,lonPer);

Where
truLon = True Longitude (rad) [1 x N]
argLat = Argument of Latitude (rad) [1 x N]