Simuwave
Version 1.0.0.0 (228 KB) by
François Chaplais
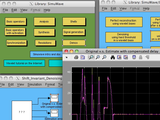
A Simulink library for wavelet processing on 1-D signals
Includes elementary blocks of filter banks, analysis and reconstruction blocks with variable scale (up to 8), demos, thresholding, differentiation in wavelet bases,
redundant wavelet processing.
This is a update to a previous version of SimuWave.
Binary .mex files must be downloaded separately (see README file).
Cite As
François Chaplais (2024). Simuwave (https://www.mathworks.com/matlabcentral/fileexchange/36152-simuwave), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Created with
R2011b
Compatible with any release
Platform Compatibility
Windows macOS LinuxCategories
Find more on Filter Banks in Help Center and MATLAB Answers
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
SimuWave/
SimuWave/Doc/
SimuWave/Filters/
SimuWave/Filters/Symlets/
SimuWave/
SimuWave/Examples/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |