PCA and ICA Package
This package contains functions that implement Principal Component Analysis (PCA) and Independent Component Analysis (ICA).
PCA and ICA are implemented as functions in this package, and multiple examples are included to demonstrate their use.
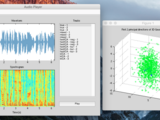
In PCA, multi-dimensional data is projected onto the singular vectors corresponding to a few of its largest singular values. Such an operation effectively decomposes the input single into orthogonal components in the directions of largest variance in the data. As a result, PCA is often used in dimensionality reduction applications, where performing PCA yields a low-dimensional representation of data that can be reversed to closely reconstruct the original data.
In ICA, multi-dimensional data is decomposed into components that are maximally independent in an appropriate sense (kurtosis and negentropy, in this package). ICA differs from PCA in that the low-dimensional signals do not necessarily correspond to the directions of maximum variance; rather, the ICA components have maximal statistical independence. In practice, ICA can often uncover disjoint underlying trends in multi-dimensional data.
Cite As
Brian Moore (2024). PCA and ICA Package (https://www.mathworks.com/matlabcentral/fileexchange/38300-pca-and-ica-package), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- AI, Data Science, and Statistics > Statistics and Machine Learning Toolbox > Dimensionality Reduction and Feature Extraction >
Tags
Acknowledgements
Inspired: EOF
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
pca_ica/
| Version | Published | Release Notes | |
|---|---|---|---|
| 2.2.0.0 | Improving implementation efficiency. |
||
| 2.1.0.0 | Adding support for audioread() function in loadAudio() |
||
| 2.0.0.0 | - Adding support for kurtosis-based Fast ICA
|
||
| 1.4.0.0 | Uploading .zip (omitted in last update) |
||
| 1.3.0.0 | Improving documentation and code performance |
||
| 1.2.0.0 | Updating myPCA() documentation |
||
| 1.1.0.0 | Fixing bug in myMultiGaussian(). Needed to use lower triangular Cholesky factorization, not the upper triangular version. |
||
| 1.0.0.0 |