Dual quaternion toolbox
The toolbox provides functions to (see the related journal article: http://www.frontiersin.org/Behavioral_Neuroscience/10.3389/fnbeh.2013.00007/abstract) :
- encode dual quaternions: a point position, velocity, a line position, velocity, a rotation, a translation, a screw,...
- do operations on dual quaternions: the dual quaternion multiplication, the dual quaternion conjugates, the inverse,...
- retrieve parameters from a dual quaternion: finding the parameters of a rotation dual quaternion, or a screw dual quaternion,...
- easily going back and forth between Fick rotation coordinates, 3*3 rotation matrices, rotation dual quaternions, angular vector
- find the shortest rotation between two unitary vectors
- find the shortest screw motion between two lines (it answers if two lines intersect, and if relevant, what the intersection point is)
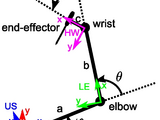
The toolbox also provides one example file (example_forward_kinematics.m) (see also the file "html/example_forward_kinematics.html"). This
example describes the forward kinematics of the end-effector of a two- or three-link arm in 3D space. The user can choose between two methods
(alternating rotation and translation dual quaternions, or using screw motion dual quaternions) to encode the forward kinematics: the results are
identical, whatever the method which is used. Furthermore, for the three-link arm, the orientation of the end-effector is also taken into account
(via line transformations).
For each of these methods and example, the user will find an extensive documentation by typing HELP NAME_OF_THE_FUNCTION in the MATLAB environment
Cite As
Guillaume Leclercq (2024). Dual quaternion toolbox (https://www.mathworks.com/matlabcentral/fileexchange/39288-dual-quaternion-toolbox), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Sciences > Neuroscience > Behavior and Psychophysics >
- Robotics and Autonomous Systems > Robotics System Toolbox > Coordinate Transformations >
- Aerospace > Aerospace Toolbox > Standard Workflow Procedures > Coordinate Systems > Quaternion Math >
Tags
Acknowledgements
Inspired: Robotics Dual Quaternion Toolbox
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
Dual quaternion toolbox v3/
Dual quaternion toolbox v3/private/
Dual quaternion toolbox v3/html/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.3.0.0 | function rotMatrix2dquat updated, such that it deals with 180 deg rotations and implements the method described in https://www.researchgate.net/publication/3298038_On_homogeneous_transforms_quaternions_and_computationalefficiency |
||
| 1.2.0.0 | I modified the following files:
|
||
| 1.1.0.0 | I provided the link (in the description) towards the journal publication linked to these methods. |
||
| 1.0.0.0 |