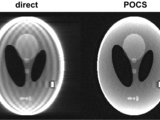
MRI Partial Fourier reconstruction with POCS
POCS (Projection Onto Convex Sets) is often used to reconstruct partial Fourier MRI data.
This implementation works with 2D or 3D data on a Cartesian grid. It is optimized for speed and automatically detects the asymmetrically sampled dimension.
Input data is generally assumed to be a multi-channel k-space signal, with the first dimension for the channels (or coils). You can, however, pass a pure 2D array.
[im, kspFull] = pocs( kspIn, iter, watchProgr )
=== Input ===
kspIn: Reduced Cartesian MRI Data-Set
Any dimension may be reduced,
but only one reduction dim. is allowed due to Physics/Math.
Allowed shapes for kspIn are...
... Ny x Nx
... Nc x Ny x Nx
... Nc x Ny x Nx x Nz
With Nc == number of receive Channels / Coils.
kspIn can either be a zero-padded array, so the partial Fourier property is obvious.
Or kspIn can be the measured data only, then we try to find k-space centre automagically
and create a zero-padded array with the full size, first.
Errors are however more likely to occur in the latter case.
iter: No. of iterations
(optional) default: iter = 20
Try on your own if larger iter improves your results!
watchProgr: true/false; Whether the progress of the reconstruction should
(optional) be monitored in an image window.
In 3D data, only the central partition will be shown.
=== Output ===
im: Reconstructed Images (channels not combined)
kspFull: Reconstructed full k-space data (just the Fourier transformed im)
Cite As
Michael Völker (2024). MRI Partial Fourier reconstruction with POCS (https://www.mathworks.com/matlabcentral/fileexchange/39350-mri-partial-fourier-reconstruction-with-pocs), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Sciences > Neuroscience > Human Brain Mapping > MRI >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.