jdugge/xy2sn
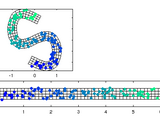
Matlab functions to transform between cartesian (xy) and curvilinear orthogonal (sn) coordinates using a spline representation of a centerline.
Cite As
Juernjakob Dugge (2024). jdugge/xy2sn (https://github.com/jdugge/xy2sn), GitHub. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Mathematics and Optimization > Mapping Toolbox > Coordinate Reference Systems >
- Radar > Mapping Toolbox > Coordinate Reference Systems >
- MATLAB > Mathematics > Computational Geometry > Cartesian Coordinate System Conversion >
- Aerospace > Aerospace Toolbox > Standard Workflow Procedures > Unit Conversions >
Tags
Acknowledgements
Inspired by: distance2curve, arclength, interparc
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
Versions that use the GitHub default branch cannot be downloaded
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.3.0.0 | The s-coordinate is no longer normalised, but uses distance units. This is consistent with Merwade's description of the method. (Thanks to Chad Greene for raising this issue) |
|
|
| 1.2.0.0 | Dramatically increased performance by using a piecewise linear approximation for the smoothed centerline. |
||
| 1.1.0.0 | Added check for a bug in "distance2curve.m" |
||
| 1.0.0.0 |