Modified & Generalized Dunn's index
This package computes the modified Dunn's internal cluster validity index using the shortest paths in the neighbourhood graph (Ilc, 2012). It also includes an implementation of the original Dunn's index (Dunn, 1973), the generalized Dunn's index (Pal & Biswas, 1997), and a bunch of algorithms for building graphs on data.
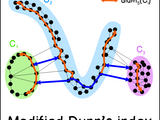
Cluster validation index is a measure of quality of a data partition that is obtained from clustering algorithm. The internal indices evaluate the given partition of the data by measuring the compactness and the separation of the clusters on a basis of some objective criteria, without any information about how the true partition should look like. Original Dunn's index (Dunn, 1973) validates clusters of data by computing the compactness within clusters (maximum distance between any two points from the same cluster) and separation between clusters (minimal distance between two data points that belong to different clusters). Pal & Biswas proposed the generalization of Dunn's index using neighbourhood graph on data. Furthermore, Ilc proposed a modification of this approach based on the shortest paths in the graph. See references for additional explanation on this topic.
Supported neighbourhood graphs for cluster validation:
- Gabriel graph
- relative neighbourhood graph
- epsilon-neighbourhood graph
- Euclidean minimum spanning tree graph
- directed kNN graph
- mutual kNN graph
- symmetric kNN graph
ACKNOWLEDGEMENTS
This package contains code contributed by the following authors, who made their work freely available:
- Matthias Hein and Ulrike von Luxburg (http://www.ml.uni-saarland.de/GraphDemo/GraphDemo.html),
- Richard E. Strauss (http://www.faculty.biol.ttu.edu/Strauss/Matlab/Matlab.htm),
- Piotr Dollar (http://vision.ucsd.edu/~pdollar/toolbox/doc/),
- Julian Ramos (http://www.mathworks.com/matlabcentral/fileexchange/27859)
Mentioned authors are greatly appreciated for their valuable contribution to this package.
REFERENCES
Ilc, N. (2012). Modified Dunn’s cluster validity index based on graph theory. Przeglad Elektrotechniczny (Electrical Review), (2), 126-131.
Pal, N. R., & Biswas, J. (1997). Cluster validation using graph theoretic concepts. Pattern Recognition, 30(6), 847-857.
Dunn, J. C. (1973). A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. Journal of Cybernetics, 3(3), 32–57.
CURRENT VERSION: 1.1
Cite As
Nejc Ilc (2024). Modified & Generalized Dunn's index (https://www.mathworks.com/matlabcentral/fileexchange/42199-modified-generalized-dunn-s-index), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Acknowledgements
Inspired by: Dunn's index
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.