Complex Function Explorer
The submission provides routines for visual exploration of complex (in particular analytic and meromorphic) functions. Basically the function values are color-coded and displayed as images either directly on the domain or on an associated surface.
The domain can be a subset of the complex plane or of the Riemann sphere, the surfaces implemented are different versions of analytic landscapes (standard, logarithmic, compressed), but the reader will find it not difficult to depict functions on Riemann surfaces.
Various color schemes (phase plots and their modifications, domain coloring, and several black-and-white patterns) are provided, which allow one to read off properties of the function easily. In particular, in many color schemes, the location of zeros, poles, saddle points (zeros of the derivative), and
essential singularities can clearly be seen.
The most convenient entrance is the graphical user interface CFEGUI, which
allows one to enter all necessary data, to control the color options, the shape of the surface and other parameters. The interface data can be saved and loaded, several examples illustrate various options.
Alternatively, some routines can be called as MATLAB functions. In that case the user must provide an array (matrix) of complex numbers z which covers the domain (typically a rectangle, a disk or an annulus) of the function, and an array of the same size with the corresponding values w=f(z). Calling
PhasePlot(z,w);
creates a phase plot of f on the domain of z. Try PPDemo to see a number of examples with different color options.
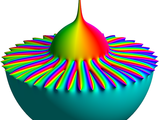
The screenshot shows a colored analytic landscape of a rational function on the Riemann sphere.
For further information and a gallery of images visit www.visual.wegert.com or consult E. Wegert: Visual Complex Functions, Birkhaeuser/Springer 2012.
Cite As
Elias Wegert (2024). Complex Function Explorer (https://www.mathworks.com/matlabcentral/fileexchange/45464-complex-function-explorer), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Control Systems > Control System Toolbox > Linear Analysis > Stability Analysis > Pole and Zero Locations >
Tags
Acknowledgements
Inspired by: Phase Plots of Complex Functions
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
Examples/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |