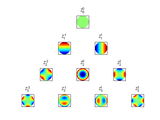
Zernike polynomials
ZERNFUN.m and ZERNFUN2.m compute the Zernike functions Znm(r,theta). These functions, which form an orthogonal basis on the unit circle, are used in disciplines such as astronomy, optics, optometry, and ophthalmology to characterize functions and data on a circular domain. ZERNPOL.m computes the Zernike polynomials Znm(r), which are the radial portion of the Zernike functions.
A MATLAB Digest article describing the use of the Zernike functions for analyzing optics data (using a LASIK surgery data as an example) also is available, on the File Exchange as a PDF,
and in HTML at:
Cite As
Paul Fricker (2024). Zernike polynomials (https://www.mathworks.com/matlabcentral/fileexchange/7687-zernike-polynomials), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Sciences > Chemistry >
- Sciences > Physics > Atomic, Molecular & Optical > Optics & Lasers > Zernike Polynomials >
- MATLAB > Mathematics > Elementary Math > Polynomials >
Tags
Acknowledgements
Inspired by: showregions.m, quadcc
Inspired: Zernike decomposition, Zernike Polynomial Coefficients for a given Wavefront using Matrix Inversion in Matlab, zernike3, Fast computation of Zernike Radial Polynomials, Zernfun2a.m, showregions.m, quadcc, iahncajigas/nSTAT
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.