geom2d
Editor's Note: This file was selected as MATLAB Central Pick of the Week
Geometry library to handle and visualize geometric primitives such as points, lines, circles and ellipses, polylines and polygons...
The goal is to provide a low-level library for manipulating geometrical primitives, making easier the development of more complex geometric algorithms.
The library proposes functions to:
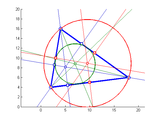
* create various shapes (points, circles, lines, ellipses, polylines, polygons) using an intuitive syntax. Ex: createCircle(p1, p2, p3) to create a circle through 3 points, create parallel and perpendicular lines
* compute intersections between 2 lines, between a line and a circle
* work on polylines and polygons: compute centroid and area, expand, clip with half-plane...
* measure distances (between points, a point and a line, a point and a group of points), angle (of a line, between 3 points), or test geometry (point on a line, on a circle).
* manipulate planar transformations. Ex: P2 = transformPoint(P1, createRotation(CENTER, THETA));
* draw shapes easily. Ex: drawCircle([50 50], 25), drawLine([X0 Y0 DX DY]). Some clipping is performed for infinite shapes such as lines or rays.
Additional help is provided in geom/Contents.m file, as well as summary files like 'points2d.m' or 'lines2d.m'.
Note: the project has merged with the geom3d library (FeX 24484), and is now hosted on GitHub: https://github.com/mattools/matGeom
Cite As
David Legland (2024). geom2d (https://www.mathworks.com/matlabcentral/fileexchange/7844-geom2d), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- MATLAB > Mathematics > Graph and Network Algorithms > Construction >
- MATLAB > Mathematics > Computational Geometry > Elementary Polygons >
- Sciences > Mathematics > Geometry > Computational Geometry >
Tags
Acknowledgements
Inspired by: Minimum Enclosing Circle, Curve intersections
Inspired: Split Line Segments (Edges), Geometric and Topological Methods for Significance Testing in Wavelet Analysis, Cumulative Areawise Testing in Wavelet Analysis, Chord Length Distribution from Binary 2D Images, image ellipsoid 3D, imMinkowski, Generate random line segments without intersecting
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
geom2d/demos-geom2d/triangle
geom2d/demos-polygons2d
geom2d/demos-polynomialCurves2d
geom2d/geom2d
geom2d/geom2d/private
geom2d/polygons2d
geom2d/polygons2d/private
geom2d/polynomialCurves2d
geom2d/utils
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.25 | renamed inertiaEllipse into equivalentEllipse, added principalAxes, various bug fixes. |
||
| 1.24 | new functions for polygons: polygonInertiaEllipse.m, polygonSecondAreaMoments.m, boxToPolygon ; also improves numerical precision of some functions.
|
|
|
| 1.23.1.0 | update project link |
||
| 1.23.0.0 | * added new functions: randomPointInPolygon, resamplePolygonByLength, polygonEdges
|
||
| 1.22.0.0 | various updates in header docs |
||
| 1.21.0.0 | remove license statements |
||
| 1.20.0.0 | add missing utility directory, update description |
||
| 1.19.0.0 | update computation of polygon/polyline self-intersections, add registerICP for Iterative Closest Point registration, add some functions (polygonSymmetryAxis, signatureToPolygon).
|
||
| 1.18.0.0 | update medialAxisConvex, add smoothPolygon, smoothPolyline, findClosestPoint functions |
||
| 1.17.0.0 | fix several bugs (clipEdge, removeMultipleVertices...), various doc update, add some demos for polynomial curves |
|
|
| 1.16.0.0 | various code cleanup and doc updates |
||
| 1.15.0.0 | lot of code cleanup, new functions for working with polygons, clean up drawing functions |
||
| 1.14.0.0 | fixed bugs in intersectLineCircle, added minimumCaliperDiameter and averagePointSet of a set of points. Now uses degrees for representing shapes |
||
| 1.13.0.0 | split library in several packages, add several functions (circle and circle-line intersections, computation of inertia ellipse) |
||
| 1.12.0.0 | fix bugs (intersectLines, isPointOnEdge), remove obsolete licence considerations |
||
| 1.11.0.0 | bug fixes (isPointOnEdge, intersectPolylines), remove obsolete licence info |