Simulink Control Design lets you design and analyze control systems modeled in Simulink. You can automatically tune arbitrary SISO and MIMO control architectures, including PID controllers. PID autotuning can be deployed to embedded software for automatically computing PID gains in real time. You can also implement active disturbance rejection control, extremum-seeking control, and model reference adaptive control algorithms for applications where the controller must adapt to changing plant and disturbance dynamics.
You can find operating points and compute exact linearizations of Simulink models at various operating conditions. Simulink Control Design provides tools that let you compute simulation-based frequency responses without modifying your model.
PID Controller Tuning
Automatically tune PID controllers in a Simulink model using the PID Tuner app. Deploy and run the PID tuning algorithm on your embedded hardware by generating C code for the Closed-Loop PID Autotuner block.
Classical Control Design
Tune SISO control loops in Simulink using graphical, automated tuning tools with the Control System Designer app.
Multiloop, Multiobjective Tuning
Automatically tune arbitrary SISO and MIMO decentralized control structures modeled in Simulink to satisfy time and frequency domain design requirements using the Control System Tuner app.
Gain Scheduling
Automatically tune gain-scheduled controllers for nonlinear or time-varying plants to meet performance requirements throughout your system’s operating envelope.
Data-Driven Control
Implement data-driven, learning-based control techniques with Simulink blocks for active disturbance rejection control, extremum-seeking control, model reference adaptive control, and constraint enforcement.
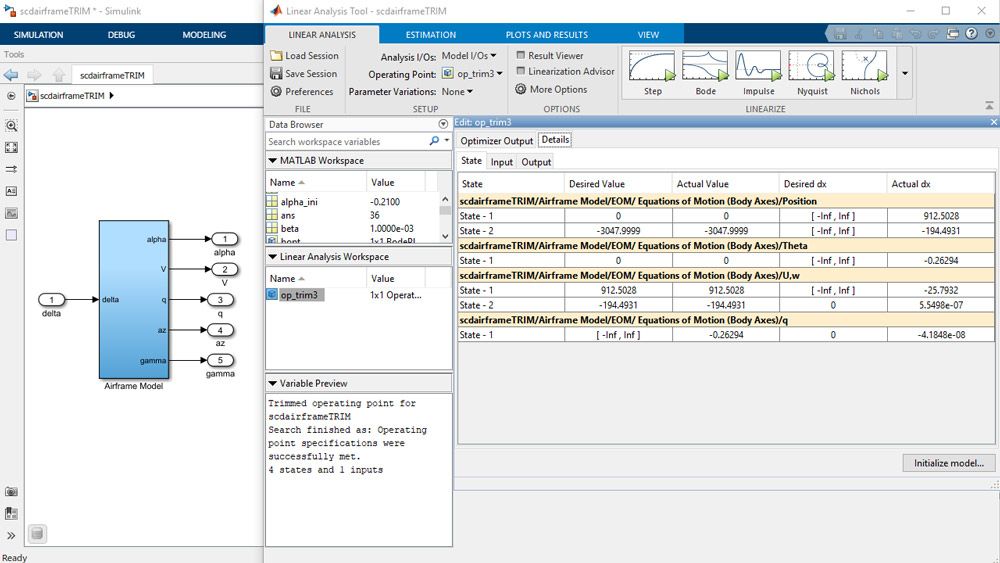
Operating Points
Find the operating points of your Simulink model using specifications or simulation times. Use the Steady State Manager app to interactively trim your model from state, input, and output specifications.
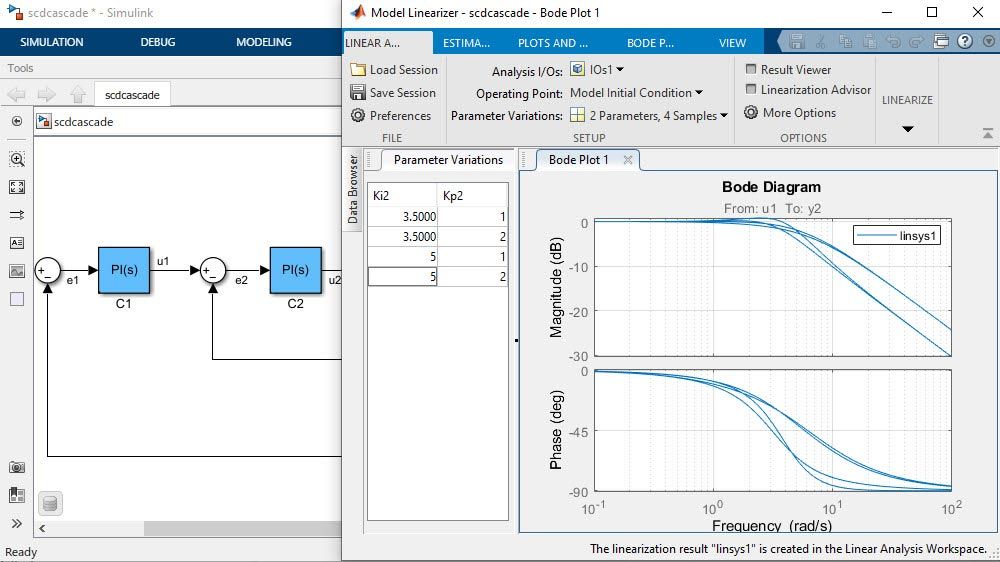
Linearization
Linearize continuous, discrete, and multirate Simulink models using the Model Linearizer app. Identify and fix common linearization issues using the LinearizationAdvisor object.
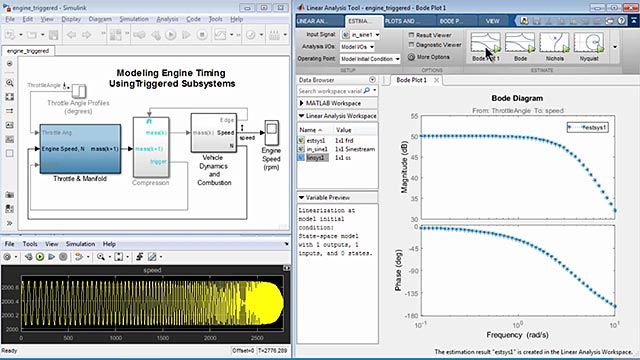
Frequency Response Estimation
Estimate frequency responses and examine frequency domain characteristics of Simulink models using input-output data. Deploy your estimation algorithm as an embedded application for real-time estimation of a physical plant.
Reference Applications
Use reference application examples for flight control, power electronics, robotics, and other applications to design and analyze controllers for systems modeled in Simulink.
Product Resources:
"MathWorks tools helped us to simplify our design process by providing an integrated environment for creating the innovative technical features that our customers demand."
Laurence Lane, Haldex
Get a Free Trial
30 days of exploration at your fingertips.
Ready to Buy?
Get pricing information and explore related products.
Are You a Student?
Your school may already provide access to MATLAB, Simulink, and add-on products through a campus-wide license.