Have questions? Contact sales.
Wavelet Toolbox provides apps and functions for the time-frequency analysis of signals and multiscale analysis of images. You can denoise and compress data, and detect anomalies, change-points, and transients. The toolbox enables data-centric artificial intelligence (AI) workflows by providing time-frequency transforms and automated feature extraction, including scattering transforms, continuous wavelet transforms (scalograms), Wigner-Ville distribution, and empirical mode decomposition. You can extract edges and oriented features from images using wavelet, wavelet packet, and shearlet transforms.
The apps let you interactively perform time-frequency analysis, signal denoising, or image analysis, and generate MATLAB scripts to reproduce or automate your work.
You can generate C/C++ and CUDA® code from toolbox functions for embedded deployment.
Machine Learning and Deep Learning with Wavelets
Derive low-variance features from real-valued time series and image data for classification and regression with machine learning and deep learning models. Use continuous wavelet analysis to generate 2D time-frequency maps of time series data, which can be used as inputs to deep convolutional neural networks (CNN).
Time-Frequency Analysis
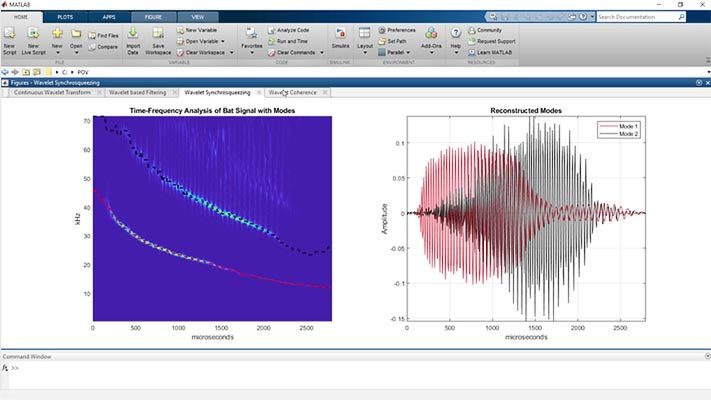
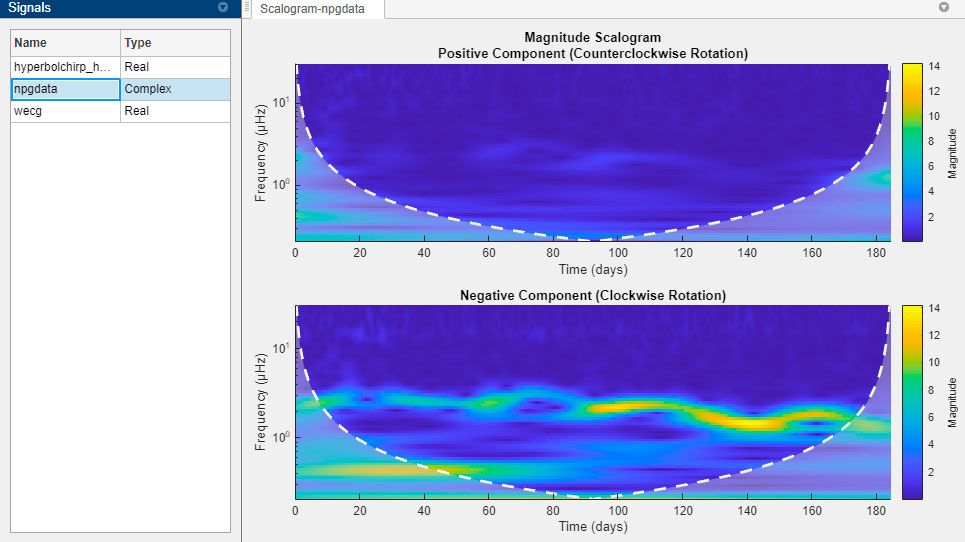
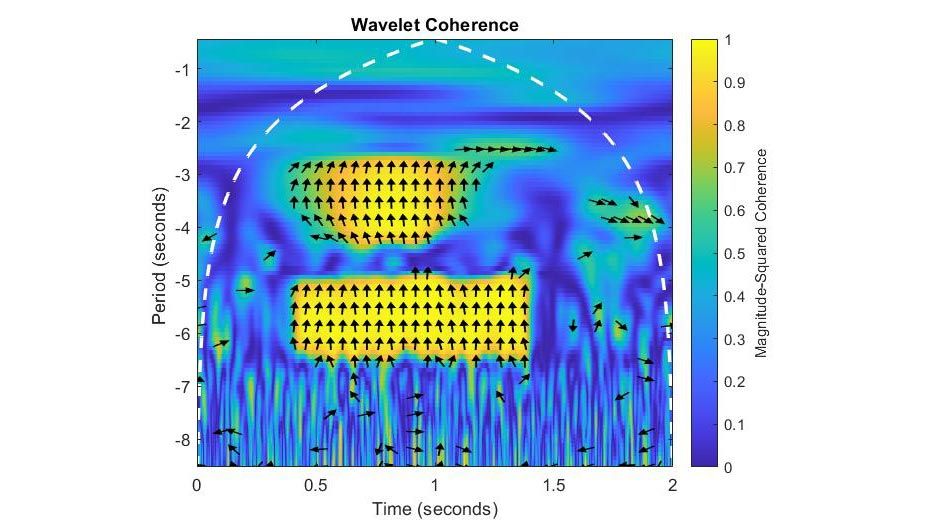
Analyze signals jointly in time and frequency and images jointly in space, spatial frequency, and angle with the continuous wavelet transform (CWT). Use the Time-Frequency Analyzer app to visualize scalograms of real- and complex-valued signals. Perform adaptive time-frequency analysis using nonstationary Gabor frames with the constant-Q transform (CQT).
Discrete Multiresolution Analysis
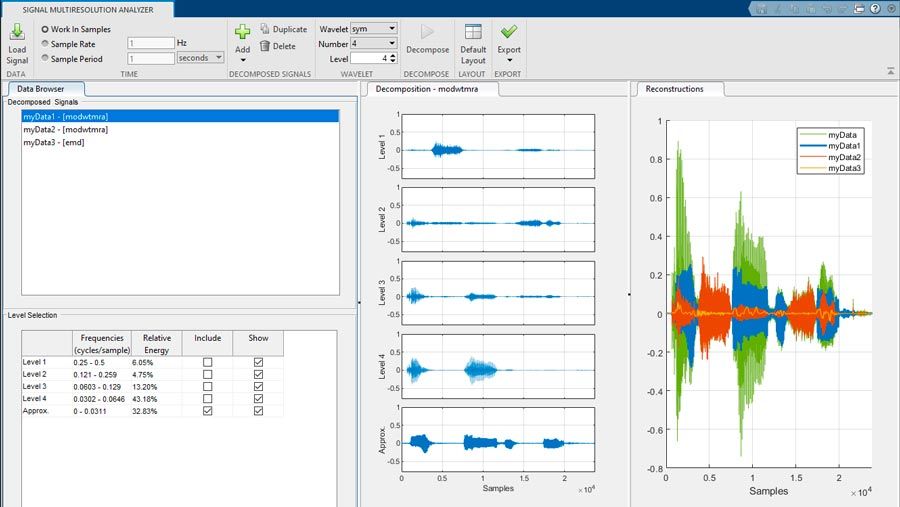
Use the decimated discrete wavelet transform (DWT) to analyze signals, images, and 3D volumes in progressively finer octave bands. Implement nondecimated wavelet transforms. Decompose nonlinear or nonstationary processes into intrinsic modes of oscillation using empirical mode decomposition (EMD).
Filter Banks
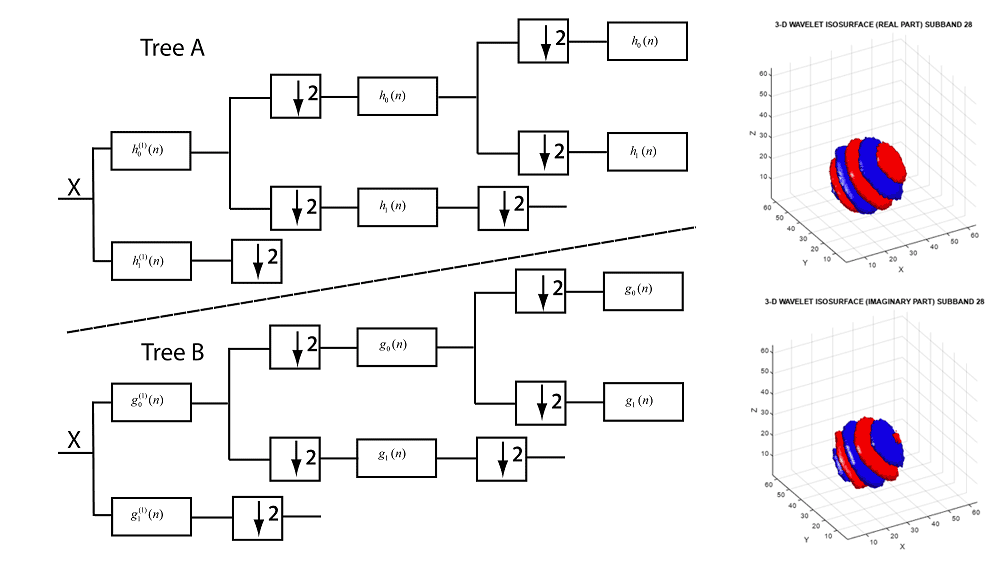
Use dual-tree filter banks to enhance directional selectivity in images. Design custom filter banks using the lifting method. Lifting also provides a computationally efficient approach for analyzing signals and images at different resolutions or scales.
Denoising and Compression
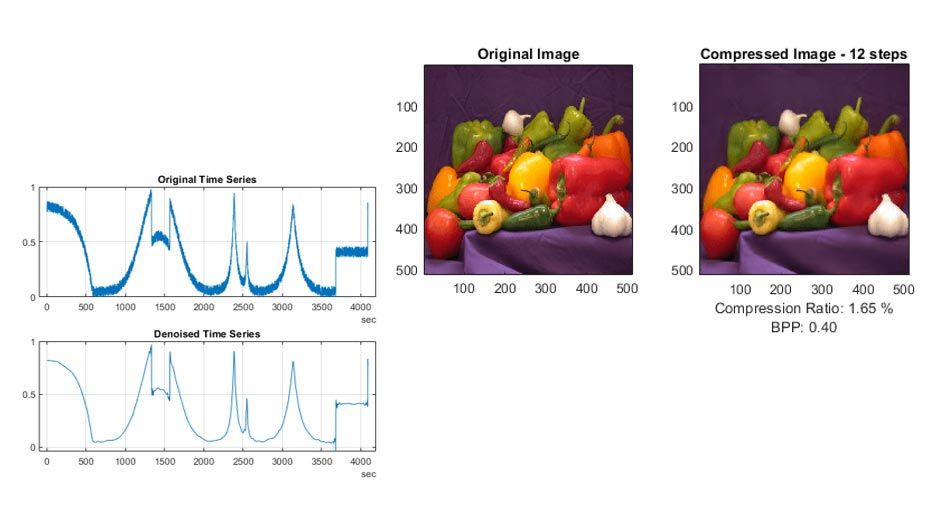
Use wavelet and wavelet packet denoising techniques to retain features that are removed or smoothed by other denoising techniques. The Wavelet Signal Denoiser app lets you visualize and denoise 1D signals. Use wavelet and wavelet packet algorithms to compress signals and images by removing data without affecting perceptual quality.
Acceleration and Deployment
Speed up your code by using GPU and multicore processors for supported functions. Use MATLAB Coder to generate standalone ANSI-compliant C/C++ code from Wavelet Toolbox functions that have been enabled to support C/C++ code generation. Generate optimized CUDA code to run on NVIDIA® GPUs for supported functions.
Product Resources:
Get a Free Trial
30 days of exploration at your fingertips.
Ready to Buy?
Get pricing information and explore related products.
Are You a Student?
Your school may already provide access to MATLAB, Simulink, and add-on products through a campus-wide license.