Analyzing LASIK Optical Data Using Zernike Functions
By Paul Fricker, MathWorks
Researchers in fields as diverse as optometry, astronomy, and photonics face a common challenge: how to accurately measure structural deformations in circular optical elements such as ocular lenses or corneas (in optometry), mirrors (in astronomy) or optical fibers (in photonics), or the aberrations in optical wavefronts caused by these deformations.
In optical systems, both the measurement devices, which are constructed using lenses, optical fibers, or other optical components, and the subjects being measured, such as a patient’s eye or a telescope mirror, are often circular. As a result, measurement data is usually expressed over a circular domain. When researchers need to characterize the structure of measured deformations and aberrations using Fourier analysis they most often use Zernike functions because these form a complete, orthogonal basis over the unit circle.
Using pre- and post-operative corneal topography data from a LASIK surgery patient as an example, this article describes the modal analysis of optics data using Zernike functions implemented in MATLAB. The Zernike function M-files used in this article are available for download. Using these M-files, computing the spectrum of Zernike modal amplitudes can be performed with a few simple lines of MATLAB code.
Computing Modal Coefficients with Zernike Functions
The Zernike functions (Figure 1) are a product of the Zernike radial polynomials and sine- and cosine-functions,
\[\begin{equation}\left\{\begin{array}{l} Z_n^m(r,\theta) \\ Z_n^{-m}(r,\theta) \end{array}\right\} = R_n^m(r) \left\{\begin{array}{l}\sin(m\theta)\\ \cos(m\theta)\end{array}\right\}\\\end{equation}\tag{1}\]
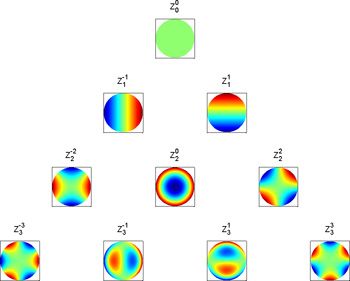
The index n = 0,1,2,… is called the degree of the function or polynomial, while m = -n to +n, with (n-m) even, is called the order. The radial polynomials are usually defined using their series representation as a finite sum of powers of r2:
\[R_n^m(r) = \sum_{k=0}^{\frac{n-m}{2}}\frac{(-1)^k(n-k)!}{k!\left(\frac{n+m}{2} - k\right)!\left(\frac{n-m}{2} - k\right)!}r^{n-2k}\qquad n=0,1,2,\ldots\qquad (n-m) \quad \text{even}\]
Although this expression looks complicated, the \(R_n^m(r)\) are, in fact, simple polynomials (Table 1).
| \(R_0^0(r)\) | 1 |
| \(R_1^1(r)\) |
\(r\) |
| \(R_2^0(r)\) |
\(2r^2 – 1\) |
| \(R_2^2(r)\) |
\(r^2\) |
| \(R_3^1(r)\) |
\(3r^3 – 2r\) |
| \(R_3^3(r)\) |
\(r^3\) |
Table 1. The first six Zernike radial polynomials
The first 10 Zernike functions, evaluated using equation 1, are listed in Table 2. The low mode number functions are used so frequently for analyzing optical data that many are given common names.
| \(Z_0^0(r,\theta)\) | 1 | |
| \(Z_1^{-1}(r,\theta)\) |
\(r \sin \theta\) | y-tilt |
| \(Z_1^1(r,\theta)\) |
\(r \cos \theta\) | x-tilt |
| \(Z_2^{-2}(r,\theta)\) |
\(r^2 \sin 2\theta\) | astigmatism |
| \(Z_2^0(r,\theta)\) |
\(2r^2 – 1\) | defocus |
| \(Z_2^2(r,\theta)\) |
\(r^2 \cos 2\theta\) | astigmatism |
| \(Z_3^{-3}(r,\theta)\) |
\(r^3 \sin 3\theta\) | trefoil |
| \(Z_3^{-1}(r,\theta)\) |
\((3r^3 – 2r) \sin \theta\) | coma |
| \(Z_3^1(r,\theta)\) |
\((3r^3 – 2r) \cos \theta\) | coma |
| \(Z_3^3(r,\theta)\) |
\(r^3 \cos 3\theta\) | trefoil |
Table 2. The first ten Zernike radial functions and their common names.
These functions are useful as a basis for decomposing complex functions or data because they are orthogonal over the unit circle, meaning that they satisfy the following relation:
\[\iint\limits_{\text{circle}} Z_n^m(r,\theta) Z_{n'}^{m'}(r,\theta) r \mathrm{d}r \mathrm{d}\theta = \frac{1}{2n+1}\delta_{n,n'} \delta_{m,m'} \]
The factor \((2n+1)^{-1}\) on the right is usually used as a normalization constant for the functions. Using this orthogonality, any function \(f(r,\theta)\)defined on the circle can be expressed as a sum of Zernike modes, just as sine and cosine functions are used in familiar 1-D Fourier analysis
\[\begin{equation}f(r,\theta) = \sum_{n=0}^{\infty} \sum_{m=-n}^{n} a_{nm} Z_n^m(r,\theta)\end{equation}\tag{2}\]
By representing data in this way we can summarize a complicated structural deformation or aberration in terms of a small number of coefficients associated with the dominant Zernike modes.
The coefficients in Equation 2 are evaluated by inverting the equation,
\[ a_{nm} = \iint\limits_{\text{circle}} f(r,\theta) Z_{n}^{m}(r,\theta) r \mathrm{d}r \mathrm{d}\theta \]
The \(a_{nm}\)can be determined directly from this expression if \(f(r,\theta)\) is a known function, or computed numerically if \(f\) is a set of measurement data. In the latter case, the formal approach to computing these integrals is to use a numerical quadrature routine.
In our example, we use a faster and simpler alternative: we analyze the LASIK surgery data by computing approximate coefficients, evaluated by truncating the original summation after a finite number of terms N, and compute the required Zernike functions at the data grid point locations \((r_i\theta_i)\).
\[f(r_i,\theta_i) = \sum_{p=1}^n a_p Z_p(r_i,\theta_i) \qquad \rightarrow \qquad f = Z \cdot a\]
This truncation produces an overdetermined system of linear equations in the unknown coefficients \(a_p\), which we can solve as a matrix equation using the MATLAB left matrix division operator,
a=Z\f
This operator computes the numerical solution to this system in the least squares sense. Since this calculation is essentially a regression analysis, the computed coefficient values depend on the number and nature of the basis functions that we use. Therefore, after completing the analysis we must confirm whether we have used enough Zernike modes to accurately characterize the original data.
Analyzing Corneal Topography Data
The corneal topography data was collected before and after a patient underwent LASIK surgery to correct an astigmatism. The patient has a significant primary corneal astigmatism in each eye (Figure 2). Zernike analysis will enable us to quantify the size of the corneal deformation before surgery and to assess whether the surgery was successful.
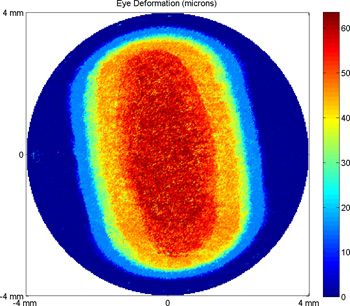
Figure 2. Corneal topography of the left eye prior to LASIK surgery. The large oval-shaped deformation is an astigmatism, which causes blurry vision due to improper focusing of the light rays entering the eye.
Computing the Zernike Spectrum
We could use any number of Zernike modes to compute the Zernike spectrum. We will use the first 36 modes, which correspond to the full set of functions from n = 0 to n = 7, as this is the set most commonly used in practice.
The number of modes required to accurately characterize the data is dictated by features of the data itself, particularly the amount of fine-scale structure. Once we have decided how many modes to use in the analysis, we can easily assess the quality of the resulting data fit by using the computed Zernike spectrum to reconstruct the data and comparing the reconstruction to the original. However, since the coefficients will be computed using a least squares fitting procedure, we must use all the functions from (n,m) = (0,0) to (n,m) = (7,7) inclusive.
Preprocessing the Data
The scanned image data has been resampled onto a 301 x 301 grid to keep the size of the data manageable. The data has been cropped so that the center of the eye is at the center of the data matrix, and the edges of the matrix correspond to the boundary of the pupil.
Computing the Modal Coefficients
We begin by creating grid coordinate matrices expressed in polar coordinates.
L = size(eyedata,1); X = -1:2/(L-1):1; [x,y] = meshgrid(X); x = x(:); y = y(:); [theta,r] = cart2pol(x,y);
Next, we compute the required degree and order values from n = 0 to n = 7, inclusive.
N = []; M = []; for n = 0:7 N = [N n*ones(1,n+1)]; M = [M -n:2:n]; end
Finally, using the function zernfun.m, we compute the required Zernike functions for all grid points within the unit circle using the MATLAB left divide operator “\”.
is_in_circle = ( r <= 1 ); Z = zernfun(N,M,r(is_in_circle),theta(is_in_circle)); a = Z\eyedata(is_in_circle);
Figure 3 shows the computed coefficients.
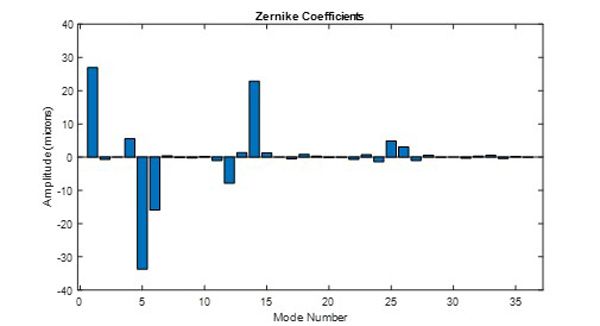
Figure 3. Spectrum of Zernike coefficients for the pre-operative eye data shown in Figure 2. The dominant modes in the data include index (n,m) = 1 (0,0) ; 4 (2,-2) ; 5 (2,0) ; 6 (2,2) ; 12 (4,-2) ; 14 (4,0) ; 25 (6,0).
In addition to the constant offset \(Z_0^0\), the dominant modes in the data include the astigmatism and defocus \((Z_2^{\pm 2})\) and defocus \((Z_2^0)\), the secondary astigmatism \((Z_4^{\pm 2})\), and the much higher-order \(Z_6^0\) mode.
Evaluating the Results
To quickly assess the quality of the results, we reconstruct the topology data from the computed Zernike coefficients and compare it to the original.
reconstructed = NaN(size(eyedata)); reconstructed(is_in_circle) = Z*a;
Qualitatively, the agreement between the original and the reconstructed data is very good (Figure 4).

Figure 4. Reconstructed corneal topology data, using the (finite) spectrum of Zernike coefficients shown in Figure 3
Numerically, we can estimate the quality of the fit by calculating the absolute difference between the original and derived data sets and normalizing by the maximum difference value (Figure 5).

Figure 5. Rough metric showing the quality of the data fit. The x-axis is a count of pixel number, normalized by the total number of pixels within the unit circle, and the y-axis is the difference between the measured and reconstructed corneal deformation at each pixel, normalized by the maximum observed difference.
Comparing Pre- and Post-Surgery Data Analysis Results
The post-LASIK-surgery corneal topography data for the patient’s left eye is shown in Figure 6.

Figure 6. Corneal topography of the left eye after LASIK surgery.
Clearly, the surgery has removed most of the corneal deformation observed in the original data. To quantify the improvement, we compute the Zernike spectrum using exactly the same procedure that we used on the pre-surgery data.
Figure 7 shows that the large amplitudes associated with the primary and secondary astigmatisms have been eliminated.

Figure 7. Zernike coefficients derived from the post-operative corneal topography in Figure 6.
Overall, the amplitudes in the post-operative data are smaller than those in the pre-operative data. Any remaining small modal amplitudes are caused by remnants of the original deformation around the perimeter of the affected area. Fortunately, these ridges are very small and are away from the central axis of the eye.
Optics Data Analysis and MATLAB
The example in this article demonstrates how practitioners, physicians, and medical researchers can use MATLAB to investigate the structure and important features of their measured aberration and deformation data. The numerical analysis techniques described in this article can be used in all fields of optics, from astronomy to photonics, to medical optics. For optical scientists and engineers who want greater control over the manipulation of their data or who need to perform custom analyses not provided by their measurement instruments, MATLAB is an ideal tool for developing an efficient, robust implementation of optics functionality like the Zernikes, and for using these tools to characterize their data.
The Zernike function M-files used in this article are available for download.
Frits Zernike (1888–1966)
Frederik (Frits) Zernike was born in Amsterdam on July 16, 1888. He graduated with a doctorate in chemistry from the University of Amsterdam in 1915. That same year, Zernike became a lecturer in physics at the University of Groningen, becoming a full professor in 1920.
For the next decade, Zernicke focused his research on statistical mechanics, turning to optics in the 1930s. He invented phase contrast microscopy, a technique that exploits the phase differences produced by different materials or tissues when diffracting light. These phase differences, which cause changes in intensity, can be used to image living tissue without using dyes or stains.
Zernike received a patent for this invention in 1936, and was awarded the Nobel Prize in 1953. He received numerous other awards and honors, including an honorary doctorate in Medicine from the University of Amsterdam, and the Rumford Medal from the Royal Society in 1952. He became a Fellow of the Royal Society in 1956.
Glossary of Terms
Zernike functions, denoted \(Z_n^m (r,θ)\), are an infinite set of orthogonal functions defined on the unit circle \(r \in [0,1], \theta \in [0,2\pi]\). Because of their orthogonality, and because the set of Zernikes provides a function for every allowed (n,m)-pair, they are the most commonly used basis for performing modal analyses of optics data.
Astigmatism is an abnormal curvature in the shape of the cornea or lens, usually due to an ellipsoidal or egg-shaped distortion of the eye. This deformation blurs the vision because it prevents light rays entering the eye at different locations from meeting at the correct point.
LASIK surgery (laser-assisted in situ keratomileusis) corrects the shape of the eye by removing thin layers of tissue from the corneal stroma, the thick middle layer of the cornea.
Corneal topography measurements are used before surgery to identify the amount of corrective reshaping that must be performed.
Published 2008 - 91544v00