The Origins of MATLAB
By Cleve Moler, MathWorks
With 2004 marking the 20th anniversary of The MathWorks, it’s a good time to look back at the origins of MATLAB.
MATLAB is now a full-featured technical computing environment, but it started as a simple “Matrix Laboratory.” Three men, J. H. Wilkinson, George Forsythe, and John Todd, played important roles in the origins of MATLAB. Our account begins more than 50 years ago.
Wilkinson was a British mathematician who spent his entire career at the National Physical Laboratory (NPL) in Teddington, outside London. Working on a simplified version of a sophisticated design by Alan Turing, Wilkinson and colleagues at NPL built the Pilot Automatic Computing Engine (ACE), one of Britain’s first stored-program digital computers. The Pilot ACE ran its first program in May 1950. Wilkinson did matrix computations on the machine and went on to become the world’s leading authority on numerical linear algebra.
At about the same time, mathematicians at the Institute for Numerical Analysis (INA), a branch of the National Bureau of Standards, located at UCLA, were working with the Standards Western Automatic Computer (SWAC), one of the USA’s first computers. Researchers at INA included George Forsythe, John Todd, and Olga Taussky-Todd. When the INA dissolved in 1957, Forsythe joined the faculty at Stanford and the Todds joined the faculty at Caltech.


I went to Caltech as a freshman in 1957 and two years later took John Todd’s Math 105, Numerical Analysis. We did some of our homework with mechanical calculators, but we also used the Burroughs 205 Datatron, one of only a few dozen computers in southern California at the time.

One of the projects that I did under Todd’s direction in 1960 involved Hilbert matrices. These are famous, ill-conditioned test matrices with elements
\[h_{i,j} = \frac{1}{i+j-1}\text{, }i,j = 1,\dots, n\]
I wrote my programs in absolute numeric machine language and punched them on paper tape. If I’d had MATLAB at the time, my project would have involved computing
H = single(hilb(6))
H =
1.0000000 0.5000000 0.3333333 0.2500000 0.2000000 0.1666667
0.5000000 0.3333333 0.2500000 0.2000000 0.1666667 0.1428571
0.3333333 0.2500000 0.2000000 0.1666667 0.1428571 0.1250000
0.2500000 0.2000000 0.1666667 0.1428571 0.1250000 0.1111111
0.2000000 0.1666667 0.1428571 0.1250000 0.1111111 0.1000000
0.1666667 0.1428571 0.1250000 0.1111111 0.1000000 0.0909091
I would then compute the inverse of H.
inv(H)
ans =
35.80 -624.43 3322.96 -7464.7 7455.6 -2731.09
-624.41 14546.09 -87179.65 209060.31 -217634.53 82038.44
3322.81 -87180.05 557732.38 -1393901.88 1493100.13 -574728.88
-7464.46 209065.14 -1393927.13 3584568 -3920712 1533448.13
7455.48 -217644.66 1493161.5 -3920799.75 4357413 -1725818
-2731.10 82044.3 -574766 1533516.5 -1725855.38 690537.44
The exact inverse of the Hilbert matrix has integer elements. A function in MATLAB computes it with a recursive algorithm.
invhilb(6)
ans =
36.00 -630.00 3360.00 -7560.00 7560.00 -2772.00
-630.00 14700.00 -88200.00 211680.00 -220500.00 83160.00
3360.00 -88200.00 564480.00 -1411200.00 1512000.00 -582120.00
-7560.00 211680.00 -1411200.00 3628800.00 -3969000.00 1552320.00
7560.00 -220500.00 1512000.00 -3969000.00 4410000.00 -1746360.00
-2772.00 83160.00 -582120.00 1552320.00 -1746360.00 698544.00
I would compare these last two matrices and say the difference was the result of roundoff error introduced by the inversion process. I was wrong. I would learn a few years later from Wilkinson that the roundoff error introduced in computing H in the first place has more effect on the final answer than the error introduced by the inversion process.
In 1961, it was time for graduate school. Todd recommended that I go to Stanford and work with his friend George Forsythe. At the time, Forsythe was a professor in the math department, but he was starting the process that would create Stanford’s computer science department, one of the world’s first, in 1965.
In 1962, after Forsythe’s numerical analysis course and a visit to Stanford by Wilkinson, I wrote a Fortran program to solve systems of simultaneous linear equations. Decks of punched cards for the program were distributed fairly widely at the time, including via SHARE, the IBM User’s Group.

Alston Householder from Oak Ridge National Laboratory and the University of Tennessee began a series of research conferences on numerical algebra in the late 1950s. These are now held every three or four years and are called the Householder Conferences. As a graduate student, I went to the third conference in the series in 1964 and obtained a photo of the organizing committee. Much later, that photo was used in the first documentation of the image function in MATLAB.

My 1965 Ph.D. thesis under Forsythe’s direction was entitled “Finite Difference Methods for the Eigenvalues of Laplace’s Operator.” The primary example, on which both Forsythe and Wilkinson had worked earlier, was the L-shaped membrane, now the MathWorks logo.
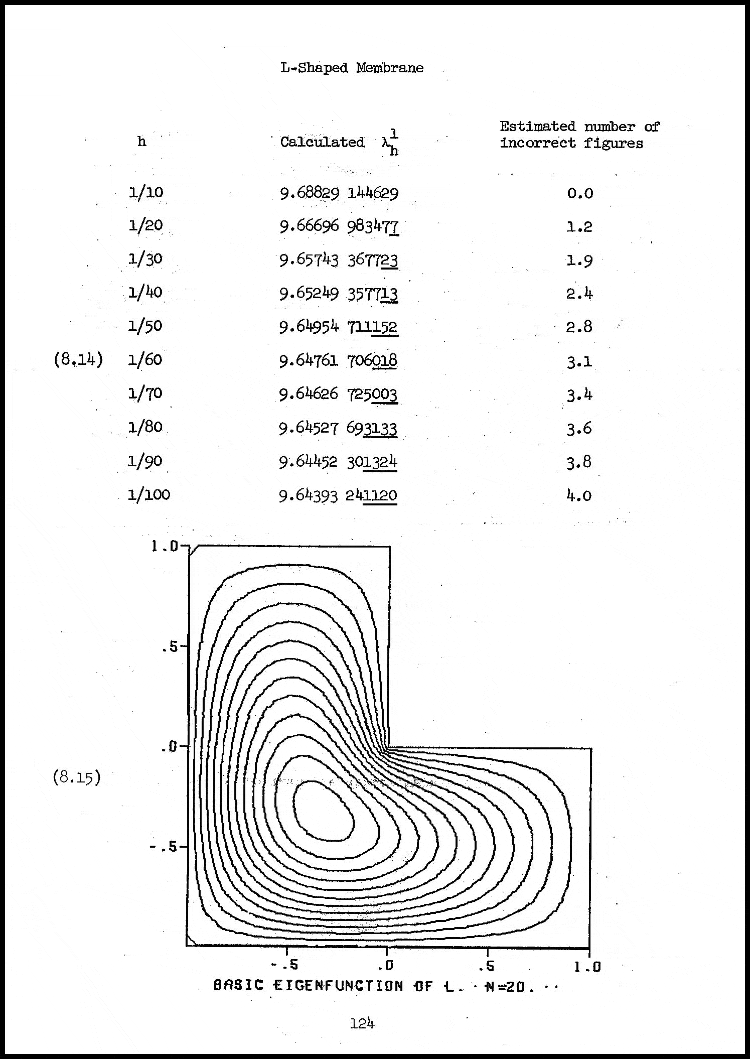
The first eigenvalue and eigenfunction of the L-shaped membrane.

Forsythe and I published a textbook about matrix computation in 1967 that was later listed by the Association for Computing Machinery as an important early text in computer science because it contained working software: programs in Algol, Fortran, and PL/I for solving systems of simultaneous linear equations.
Over several years in the late 1960s, Wilkinson and a number of colleagues published papers in Numerische Mathematik that included algorithms in Algol for various aspects of matrix computation. These algorithms were eventually collected in a 1971 book edited by Wilkinson and Reinsch.

Even today, more than 30 years after its publication, this collection of algorithms for matrix computation is an important reference.

Every summer for 15 years, Wilkinson lectured in a short course at the University of Michigan and then visited Argonne National Laboratory for a week or two. Researchers at Argonne translated the Algol code for matrix eigenvalue computation from the Wilkinson and Reinsch handbook into Fortran to produce EISPACK. This was followed by LINPACK, a package of Fortran programs for solving linear equations.



When we were developing EISPACK and LINPACK, I was a math professor at the University of New Mexico, teaching numerical analysis and matrix theory. I wanted my students to be able to use our new packages without writing Fortran programs, so I studied a book by Niklaus Wirth to learn about parsing computer languages.

In the late 1970s, following Wirth’s methodology, I used Fortran and portions of LINPACK and EISPACK to develop the first version of MATLAB. The only data type was “matrix.” The HELP command listed all of the available functions, with their names abbreviated.
ABS ANS ATAN BASE CHAR CHOL CHOP CLEA COND CONJ COS
DET DIAG DIAR DISP EDIT EIG ELSE END EPS EXEC EXIT
EXP EYE FILE FLOP FLPS FOR FUN HESS HILB IF IMAG
INV KRON LINE LOAD LOG LONG LU MACR MAG I NORM ONES
ORTH PINV PLOT POLY PRIN PROD QR RAND RANK RCON RAT
REAL RETU RREF ROOT ROUN SAVE SCHU SHOR SEMI SIN SIZE
SQRT STOP SUM SVD TRIL TRIU USER WHAT WHIL WHO WHY
There were only 80 functions. There were no M-files or toolboxes. If you wanted to add a function, you had to modify the Fortran source code and recompile the entire program. Here is a sample program. If you change long to format long, it works with today’s MATLAB.
n = 10 J = 1:n; J = J(ones(n,1),:); I = J'; E = ones(n,n); A = E./(I-J+E/2); long S = svd(A)
S =
3.141592653589682
3.141592653566661
3.141592651393170
3.141592527498737
3.141587781570560
3.141459305862261
3.138952480600909
3.104107683136387
2.786915482404130
1.300969070029704
The first graphics were very primitive.
pi = 4*atan(1); x = 0:pi/40:2*pi; y = x.*sin(3*x); plot(x,y)

This first Fortran MATLAB was portable and could be compiled to run on many of the computers that were available in the late 1970s and early 1980s. We installed it on the interactive time-sharing systems that were hosted by mainframe computers at universities and national laboratories.
The first “personal computer” that I used was the Tektronix 4081, which Argonne acquired in 1978. The machine was the size of a desk and consisted of a Tektronix graphics display attached to an Interdata 7/32, the first 32-bit minicomputer. There was only 64K, that’s 64 kilobytes of memory. But there was a Fortran compiler, and so, by using memory overlay, we were able to run MATLAB.

I visited Stanford in 1979 and taught CS237, the graduate numerical analysis course. I had the students use MATLAB for some of the homework. Half of the students in the class were from math and computer science, and they were not impressed by my new program. It was based on Fortran, it was not a particularly powerful programming language, and it did not represent current research work in numerical analysis. The other half of the students were from engineering, and they liked MATLAB. They were studying subjects that I didn’t know anything about, such as control analysis and signal processing, and the emphasis on matrices in MATLAB proved to be very useful to them.
A few of the Stanford engineering students from my class joined two consulting companies in Palo Alto. These companies extended MATLAB to have more capability in control analysis and signal processing and, in the early 1980s, offered the resulting software as commercial products.
Jack Little, a Stanford- and MIT-trained control engineer, was the principal developer of one of the first commercial products based on Fortran MATLAB. When IBM announced their first PC in August, 1981, Jack quickly anticipated the possibility of using MATLAB and the PC for technical computing. He and colleague Steve Bangert reprogrammed MATLAB in C and added M-files, toolboxes, and more powerful graphics.
The three of us founded The MathWorks in California in 1984.

Published 2004