minspantree
Minimum spanning tree of graph
Description
T = minspantree(G)T, for graph G.
T = minspantree(G,Name,Value)minspantree(G,'Method','sparse') uses Kruskal’s
algorithm for calculating the minimum spanning tree.
Examples
Minimum Spanning Tree of Cube Graph
Create and plot a cube graph with weighted edges.
s = [1 1 1 2 5 3 6 4 7 8 8 8];
t = [2 3 4 5 3 6 4 7 2 6 7 5];
weights = [100 10 10 10 10 20 10 30 50 10 70 10];
G = graph(s,t,weights);
p = plot(G,'EdgeLabel',G.Edges.Weight);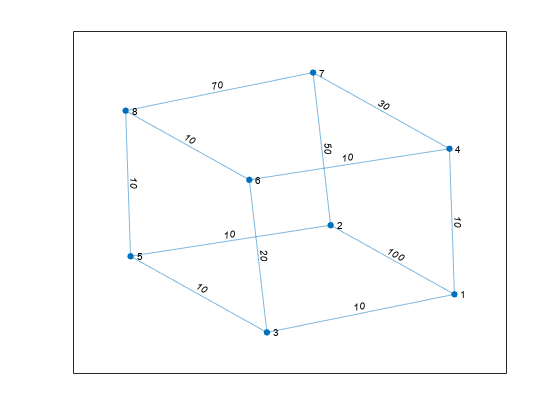
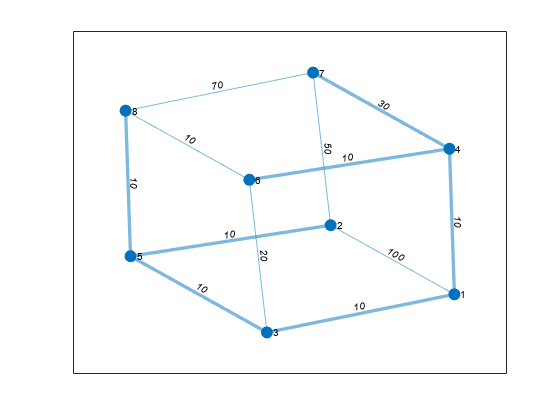
Calculate and plot the minimum spanning tree of the graph on top of the graph. T contains the same nodes as G, but a subset of the edges.
[T,pred] = minspantree(G); highlight(p,T)
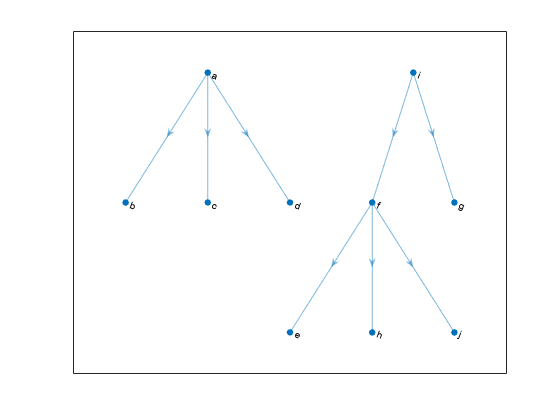
Minimum Spanning Forest from Specified Root Node
Create and plot a graph that has multiple components.
s = {'a' 'a' 'a' 'b' 'b' 'c' 'e' 'e' 'f' 'f' 'f' 'f' 'g' 'g'};
t = {'b' 'c' 'd' 'c' 'd' 'd' 'f' 'g' 'g' 'h' 'i' 'j' 'i' 'j'};
G = graph(s,t);
p = plot(G,'Layout','layered');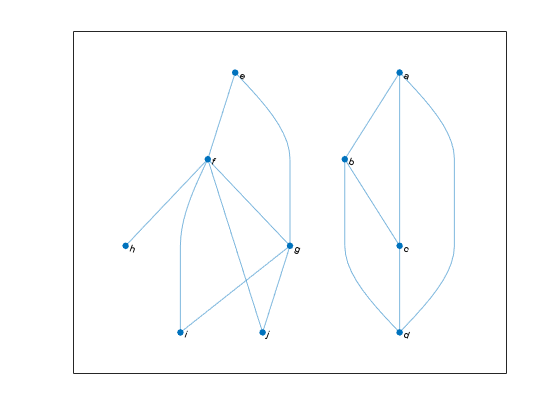
Find the minimum spanning forest for the graph, starting at node i. Highlight the resulting forest in the plot. The graph node names are carried over into the minimum spanning tree graph.
[T,pred] = minspantree(G,'Type','forest','Root',findnode(G,'i')); highlight(p,T)
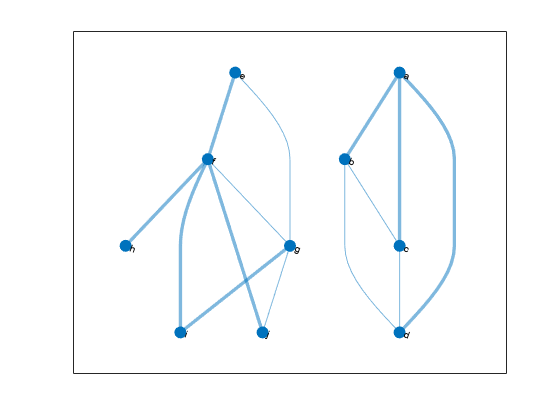
Use the vector of predecessor nodes, pred, to create a directed version of the minimum spanning forest. All of the edges in this tree are directed away from the root nodes in each component (nodes i and a).
rootedTree = digraph(pred(pred~=0),find(pred~=0),[],G.Nodes.Name); plot(rootedTree)
Input Arguments
G — Input graph
graph object
Input graph, specified as a graph object. Use graph to create an undirected graph object.
Example: G = graph(1,2)
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: [T,pred] =
minspantree(G,'Method','sparse')
Method — Minimum spanning tree algorithm
'dense' (default) | 'sparse'
Minimum spanning tree algorithm, specified as the comma-separated pair
consisting of 'Method' and one of the options in the
table.
| Option | Description |
|---|---|
'dense' (default) | Prim’s algorithm. This algorithm starts at the root node and adds edges to the tree while traversing the graph. |
'sparse' | Kruskal’s algorithm. This algorithm sorts all of the edges by weight, and then adds them to the tree if they do not create a cycle. |
Root — Root node
1 (default) | node index | node name
Root node, specified as the comma-separated pair consisting of
'Root' and a node index or node name. The default
root node is 1.
If
'Method'is'dense'(default), then the root node is the starting node.If
'Method'is'sparse', then the root node is used only to computepred, the vector of predecessor nodes.
You can specify the root node in any of these formats:
| Value | Example |
|---|---|
| Scalar node index | 1 |
| Character vector node name | 'A' |
| String scalar node name | "A" |
Type — Type of minimum spanning tree
'tree' (default) | 'forest'
Type of minimum spanning tree, specified as the comma-separated pair
consisting of 'Type' and one of the options in the
table.
| Option | Description |
|---|---|
'tree' |
Only a single tree is returned. The tree contains the root node. |
'forest' |
A forest of minimum spanning trees is returned. In
other words, specify |
Output Arguments
T — Minimum spanning tree
graph object
Minimum spanning tree, returned as a graph
object.
pred — Predecessor nodes
vector
Predecessor nodes, returned as a vector of node indices.
pred(I) is the node index of the predecessor of node
I. By convention, pred(rootNode) =
0. If Type is 'tree',
then pred(I) = NaN for all nodes I
that are not in the same component as the root node.
pred specifies a directed version of the minimum
spanning tree, with all edges directed away from the root node.
More About
Minimum Spanning Tree
For connected graphs, a spanning tree is a subgraph that connects every node in the graph, but contains no cycles. There can be many spanning trees for any given graph. By assigning a weight to each edge, the different spanning trees are assigned a number for the total weight of their edges. The minimum spanning tree is then the spanning tree whose edges have the least total weight.
For graphs with equal edge weights, all spanning trees are minimum spanning trees,
since traversing n nodes requires n-1
edges.
Extended Capabilities
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
Version History
Introduced in R2015b
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)