Introduction to MIMO Systems
This example shows Multiple-Input-Multiple-Output (MIMO) systems, which use multiple antennas at the transmitter and receiver ends of a wireless communication system. MIMO systems are increasingly being adopted in communication systems for the potential gains in capacity they realize when using multiple antennas. Multiple antennas use the spatial dimension in addition to the time and frequency ones, without changing the bandwidth requirements of the system.
For a generic communications link, this example focuses on transmit diversity in lieu of traditional receive diversity. Using the flat-fading Rayleigh channel, it illustrates the concept of Orthogonal Space-Time Block Coding, which is employable when multiple transmitter antennas are used. It is assumed here that the channel undergoes independent fading between the multiple transmit-receive antenna pairs.
For a chosen system, it also provides a measure of the performance degradation when the channel is imperfectly estimated at the receiver, compared to the case of perfect channel knowledge at the receiver.
PART 1: Transmit Diversity vs. Receive Diversity
Using diversity reception is a well-known technique to mitigate the effects of fading over a communications link. However, it has mostly been relegated to the receiver end. In [ 1 ], Alamouti proposes a transmit diversity scheme that offers similar diversity gains, using multiple antennas at the transmitter. This was conceived to be more practical as, for example, it would only require multiple antennas at the base station in comparison to multiple antennas for every mobile in a cellular communications system.
This section highlights this comparison of transmit vs. receive diversity by simulating coherent binary phase-shift keying (BPSK) modulation over flat-fading Rayleigh channels. For transmit diversity, we use two transmit antennas and one receive antenna (2x1 notationally), while for receive diversity we employ one transmit antenna and two receive antennas (1x2 notationally).
The simulation covers an end-to-end system showing the encoded and/or transmitted signal, channel model, and reception and demodulation of the received signal. It also provides the no-diversity link (single transmit- receive antenna case) and theoretical performance of second-order diversity link for comparison. It is assumed here that the channel is known perfectly at the receiver for all systems. We run the simulation over a range of Eb/No points to generate BER results that allow us to compare the different systems.
We start by defining some common simulation parameters
frmLen = 100; % frame length numPackets = 1000; % number of packets EbNo = 0:2:20; % Eb/No varying to 20 dB N = 2; % maximum number of Tx antennas M = 2; % maximum number of Rx antennas P = 2; % modulation order
and set up the simulation.
% Create comm.OSTBCEncoder and comm.OSTBCCombiner System objects(TM) ostbcEnc = comm.OSTBCEncoder; ostbcComb = comm.OSTBCCombiner; % Convert Eb/No values to SNR values. The output of the BPSK modulator % generates unit power signals. SNR = convertSNR(EbNo,"ebno","BitsPerSymbol",1); % Create comm.ErrorRate calculator System objects to evaluate BER. errorCalc1 = comm.ErrorRate; errorCalc2 = comm.ErrorRate; errorCalc3 = comm.ErrorRate; % Since the AWGN function as well as the RANDI function use the default % random stream, the following commands are executed so that the results % will be repeatable, i.e., same results will be obtained for every run of % the example. The default stream will be restored at the end of the % example. s = rng(55408); % Pre-allocate variables for speed H = zeros(frmLen, N, M); ber_noDiver = zeros(3,length(EbNo)); ber_Alamouti = zeros(3,length(EbNo)); ber_MaxRatio = zeros(3,length(EbNo)); ber_thy2 = zeros(1,length(EbNo));
% Set up a figure for visualizing BER results fig = figure; grid on; ax = fig.CurrentAxes; hold(ax,'on'); ax.YScale = 'log'; xlim(ax,[EbNo(1), EbNo(end)]); ylim(ax,[1e-4 1]); xlabel(ax,'Eb/No (dB)'); ylabel(ax,'BER'); fig.NumberTitle = 'off'; fig.Renderer = 'zbuffer'; fig.Name = 'Transmit vs. Receive Diversity'; title(ax,'Transmit vs. Receive Diversity'); set(fig, 'DefaultLegendAutoUpdate', 'off'); fig.Position = figposition([15 50 25 30]); % Loop over several EbNo points for idx = 1:length(EbNo) reset(errorCalc1); reset(errorCalc2); reset(errorCalc3); % Loop over the number of packets for packetIdx = 1:numPackets % Generate data vector per frame data = randi([0 P-1], frmLen, 1); % Modulate data modData = pskmod(data,P); % Alamouti Space-Time Block Encoder encData = ostbcEnc(modData); % Create the Rayleigh distributed channel response matrix % for two transmit and two receive antennas H(1:N:end, :, :) = (randn(frmLen/2, N, M) + ... 1i*randn(frmLen/2, N, M))/sqrt(2); % assume held constant for 2 symbol periods H(2:N:end, :, :) = H(1:N:end, :, :); % Extract part of H to represent the 1x1, 2x1 and 1x2 channels H11 = H(:,1,1); H21 = H(:,:,1)/sqrt(2); H12 = squeeze(H(:,1,:)); % Pass through the channels chanOut11 = H11 .* modData; chanOut21 = sum(H21.* encData, 2); chanOut12 = H12 .* repmat(modData, 1, 2); % Add AWGN rxSig11 = awgn(chanOut11,SNR(idx)); rxSig21 = awgn(chanOut21,SNR(idx)); rxSig12 = awgn(chanOut12,SNR(idx)); % Alamouti Space-Time Block Combiner decData = ostbcComb(rxSig21, H21); % ML Detector (minimum Euclidean distance) demod11 = pskdemod(rxSig11.*conj(H11),P); demod21 = pskdemod(decData,P); demod12 = pskdemod(sum(rxSig12.*conj(H12), 2),P); % Calculate and update BER for current EbNo value % for uncoded 1x1 system ber_noDiver(:,idx) = errorCalc1(data, demod11); % for Alamouti coded 2x1 system ber_Alamouti(:,idx) = errorCalc2(data, demod21); % for Maximal-ratio combined 1x2 system ber_MaxRatio(:,idx) = errorCalc3(data, demod12); end % end of FOR loop for numPackets % Calculate theoretical second-order diversity BER for current EbNo ber_thy2(idx) = berfading(EbNo(idx), 'psk', 2, 2); % Plot results semilogy(ax,EbNo(1:idx), ber_noDiver(1,1:idx), 'r*', ... EbNo(1:idx), ber_Alamouti(1,1:idx), 'go', ... EbNo(1:idx), ber_MaxRatio(1,1:idx), 'bs', ... EbNo(1:idx), ber_thy2(1:idx), 'm'); legend(ax,'No Diversity (1Tx, 1Rx)', 'Alamouti (2Tx, 1Rx)',... 'Maximal-Ratio Combining (1Tx, 2Rx)', ... 'Theoretical 2nd-Order Diversity'); drawnow; end % end of for loop for EbNo % Perform curve fitting and replot the results fitBER11 = berfit(EbNo, ber_noDiver(1,:)); fitBER21 = berfit(EbNo, ber_Alamouti(1,:)); fitBER12 = berfit(EbNo, ber_MaxRatio(1,:)); semilogy(ax,EbNo, fitBER11, 'r', EbNo, fitBER21, 'g', EbNo, fitBER12, 'b'); hold(ax,'off'); % Restore default stream rng(s);
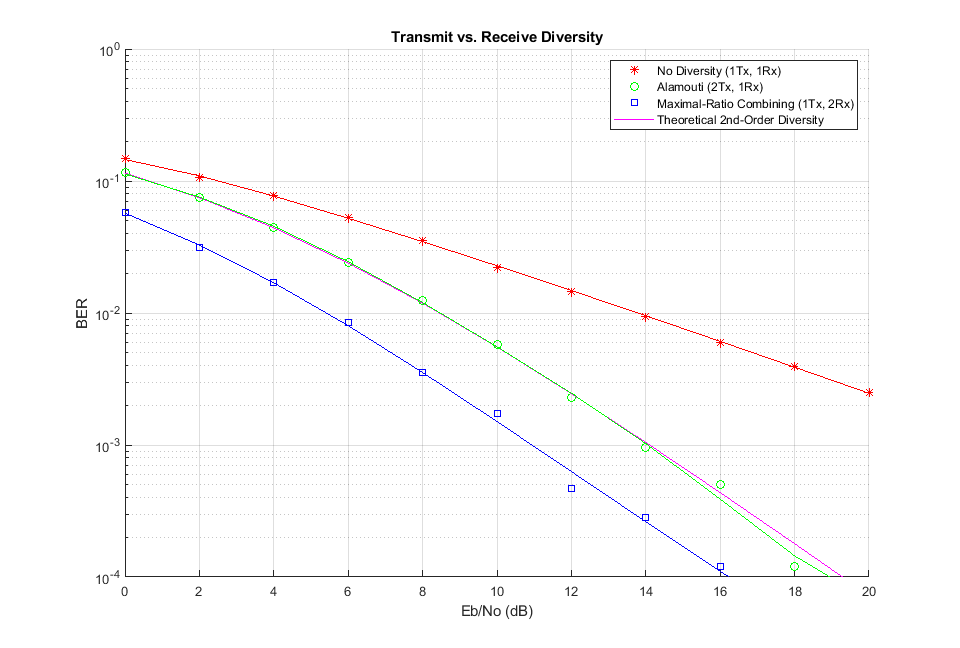
The transmit diversity system has a computation complexity very similar to that of the receive diversity system.
The resulting simulation results show that using two transmit antennas and one receive antenna provides the same diversity order as the maximal-ratio combined (MRC) system of one transmit antenna and two receive antennas.
Also observe that transmit diversity has a 3 dB disadvantage when compared to MRC receive diversity. This is because we modeled the total transmitted power to be the same in both cases. If we calibrate the transmitted power such that the received power for these two cases is the same, then the performance would be identical. The theoretical performance of second-order diversity link matches the transmit diversity system as it normalizes the total power across all the diversity branches.
The accompanying functional scripts, mrc1m.m and ostbc2m.m aid further exploration for the interested users.
PART 2: Space-Time Block Coding with Channel Estimation
Building on the theory of orthogonal designs, Tarokh et al. [ 2 ] generalized Alamouti's transmit diversity scheme to an arbitrary number of transmitter antennas, leading to the concept of Space-Time Block Codes. For complex signal constellations, they showed that Alamouti's scheme is the only full-rate scheme for two transmit antennas.
In this section, we study the performance of such a scheme with two receive antennas (i.e., a 2x2 system) with and without channel estimation. In the realistic scenario where the channel state information is not known at the receiver, this has to be extracted from the received signal. We assume that the channel estimator performs this using orthogonal pilot signals that are prepended to every packet [ 3 ]. It is assumed that the channel remains unchanged for the length of the packet (i.e., it undergoes slow fading).
A simulation similar to the one described in the previous section is employed here, which leads us to estimate the BER performance for a space-time block coded system using two transmit and two receive antennas.
Again we start by defining the common simulation parameters
frmLen = 100; % frame length maxNumErrs = 300; % maximum number of errors maxNumPackets = 3000; % maximum number of packets EbNo = 0:2:12; % Eb/No varying to 12 dB N = 2; % number of Tx antennas M = 2; % number of Rx antennas pLen = 8; % number of pilot symbols per frame W = hadamard(pLen); pilots = W(:, 1:N); % orthogonal set per transmit antenna
and set up the simulation.
% Create a comm.MIMOChannel System object to simulate the 2x2 spatially % independent flat-fading Rayleigh channel chan = comm.MIMOChannel( ... 'MaximumDopplerShift', 0, ... 'SpatialCorrelationSpecification', 'None', ... 'NumTransmitAntennas', N, ... 'NumReceiveAntennas', M, ... 'PathGainsOutputPort', true); % Change the NumReceiveAntennas property value of the hAlamoutiDec System % object to M that is 2 release(ostbcComb); ostbcComb.NumReceiveAntennas = M; % Set the global random stream for repeatability s = rng(55408); % Pre-allocate variables for speed HEst = zeros(frmLen, N, M); ber_Estimate = zeros(3,length(EbNo)); ber_Known = zeros(3,length(EbNo));
% Set up a figure for visualizing BER results fig = figure; grid on; ax = fig.CurrentAxes; hold(ax,'on'); ax.YScale = 'log'; xlim(ax,[EbNo(1), EbNo(end)]); ylim(ax,[1e-4 1]); xlabel(ax,'Eb/No (dB)'); ylabel(ax,'BER'); fig.NumberTitle = 'off'; fig.Name = 'Orthogonal Space-Time Block Coding'; fig.Renderer = 'zbuffer'; title(ax,'Alamouti-coded 2x2 System'); set(fig,'DefaultLegendAutoUpdate','off'); fig.Position = figposition([41 50 25 30]); % Loop over several EbNo points for idx = 1:length(EbNo) reset(errorCalc1); reset(errorCalc2); % Loop till the number of errors exceed 'maxNumErrs' % or the maximum number of packets have been simulated while (ber_Estimate(2,idx) < maxNumErrs) && ... (ber_Known(2,idx) < maxNumErrs) && ... (ber_Estimate(3,idx)/frmLen < maxNumPackets) % Generate data vector per frame data = randi([0 P-1], frmLen, 1); % Modulate data modData = pskmod(data,P); % Alamouti Space-Time Block Encoder encData = ostbcEnc(modData); % Prepend pilot symbols for each frame txSig = [pilots; encData]; % Pass through the 2x2 channel reset(chan); [chanOut, H] = chan(txSig); % Add AWGN rxSig = awgn(chanOut,SNR(idx)); % Channel Estimation % For each link => N*M estimates HEst(1,:,:) = pilots(:,:).' * rxSig(1:pLen, :) / pLen; % assume held constant for the whole frame HEst = HEst(ones(frmLen, 1), :, :); % Combiner using estimated channel decDataEst = ostbcComb(rxSig(pLen+1:end,:), HEst); % Combiner using known channel decDataKnown = ostbcComb(rxSig(pLen+1:end,:), ... squeeze(H(pLen+1:end,:,:,:))); % ML Detector (minimum Euclidean distance) demodEst = pskdemod(decDataEst,P); % estimated demodKnown = pskdemod(decDataKnown,P); % known % Calculate and update BER for current EbNo value % for estimated channel ber_Estimate(:,idx) = errorCalc1(data, demodEst); % for known channel ber_Known(:,idx) = errorCalc2(data, demodKnown); end % end of FOR loop for numPackets % Plot results semilogy(ax,EbNo(1:idx), ber_Estimate(1,1:idx), 'ro'); semilogy(ax,EbNo(1:idx), ber_Known(1,1:idx), 'g*'); legend(ax,['Channel estimated with ' num2str(pLen) ' pilot symbols/frame'],... 'Known channel'); drawnow; end % end of for loop for EbNo % Perform curve fitting and replot the results fitBEREst = berfit(EbNo, ber_Estimate(1,:)); fitBERKnown = berfit(EbNo, ber_Known(1,:)); semilogy(ax,EbNo, fitBEREst, 'r', EbNo, fitBERKnown, 'g'); hold(ax,'off'); % Restore default stream rng(s)
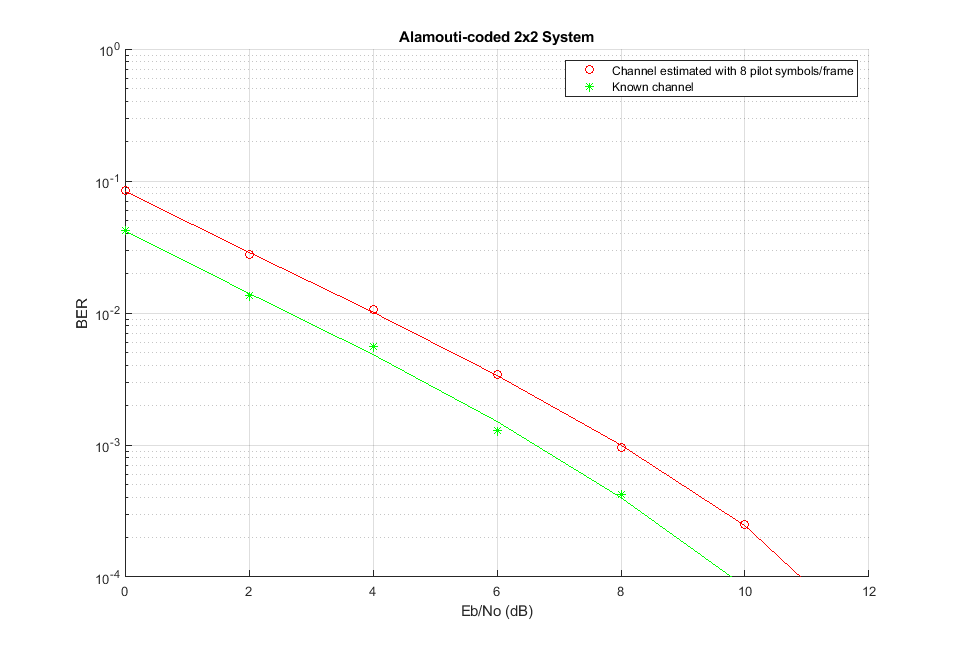
For the 2x2 simulated system, the diversity order is different than that seen for either 1x2 or 2x1 systems in the previous section.
Note that with 8 pilot symbols for each 100 symbols of data, channel estimation causes about a 1 dB degradation in performance for the selected Eb/No range. This improves with an increase in the number of pilot symbols per frame but adds to the overhead of the link. In this comparison, we keep the transmitted SNR per symbol to be the same in both cases.
The accompanying functional script, ostbc2m_e.m aids further experimentation for the interested users.
PART 3: Orthogonal Space-Time Block Coding and Further Explorations
In this final section, we present some performance results for orthogonal space-time block coding using four transmit antennas (4x1 system) using a half-rate code, G4, as per [ 4 ].
We expect the system to offer a diversity order of 4 and will compare it with 1x4 and 2x2 systems, which have the same diversity order also. To allow for a fair comparison, we use quaternary PSK with the half-rate G4 code to achieve the same transmission rate of 1 bit/sec/Hz.
These results take some time to generate on a single core. If you do not have Parallel Computing Toolbox™ (PCT) installed, we load the results from a prior simulation. The functional script ostbc4m.m is included, which, along with mrc1m.m and ostbc2m.m, was used to generate these results. If PCT is installed, these simulations are performed in parallel. In this case the functional scripts ostbc4m_pct.m, mrc1m_pct.m and ostbc2m_pct.m are used. The user is urged to use these scripts as a starting point to study other codes and systems.
[licensePCT,~] = license( 'checkout' , 'Distrib_Computing_Toolbox'); if (licensePCT && ~isempty(ver('parallel'))) EbNo = 0:2:20; [ber11, ber14, ber22, ber41] = mimoOSTBCWithPCT(100,4e3,EbNo); else load ostbcRes.mat; end % Set up a figure for visualizing BER results fig = figure; grid on; ax = fig.CurrentAxes; hold(ax,'on'); fig.Renderer = 'zbuffer'; ax.YScale = 'log'; xlim(ax,[EbNo(1), EbNo(end)]); ylim(ax,[1e-5 1]); xlabel(ax,'Eb/No (dB)'); ylabel(ax,'BER'); fig.NumberTitle = 'off'; fig.Name = 'Orthogonal Space-Time Block Coding(2)'; title(ax,'G4-coded 4x1 System and Other Comparisons'); set(fig,'DefaultLegendAutoUpdate','off'); fig.Position = figposition([30 15 25 30]); % Theoretical performance of fourth-order diversity for QPSK BERthy4 = berfading(EbNo, 'psk', 4, 4); % Plot results semilogy(ax,EbNo, ber11, 'r*', EbNo, ber41, 'ms', EbNo, ber22, 'c^', ... EbNo, ber14, 'ko', EbNo, BERthy4, 'g'); legend(ax,'No Diversity (1Tx, 1Rx), BPSK', 'OSTBC (4Tx, 1Rx), QPSK', ... 'Alamouti (2Tx, 2Rx), BPSK', 'Maximal-Ratio Combining (1Tx, 4Rx), BPSK', ... 'Theoretical 4th-Order Diversity, QPSK'); % Perform curve fitting on non-zero BER points lenBER11 = length(ber11(ber11~=0)); lenBER41 = length(ber41(ber41~=0)); lenBER22 = length(ber22(ber22~=0)); lenBER14 = length(ber14(ber14~=0)); fitBER11 = berfit(EbNo(1:lenBER11), ber11(1:lenBER11)); fitBER41 = berfit(EbNo(1:lenBER41), ber41(1:lenBER41)); fitBER22 = berfit(EbNo(1:lenBER22), ber22(1:lenBER22)); fitBER14 = berfit(EbNo(1:lenBER14), ber14(1:lenBER14)); semilogy(ax,EbNo(1:lenBER11), fitBER11, 'r', EbNo(1:lenBER41), fitBER41, 'm', ... EbNo(1:lenBER22), fitBER22, 'c', EbNo(1:lenBER14), fitBER14, 'k'); hold(ax,'off');
Starting parallel pool (parpool) using the 'Processes' profile ... Connected to parallel pool with 8 workers.
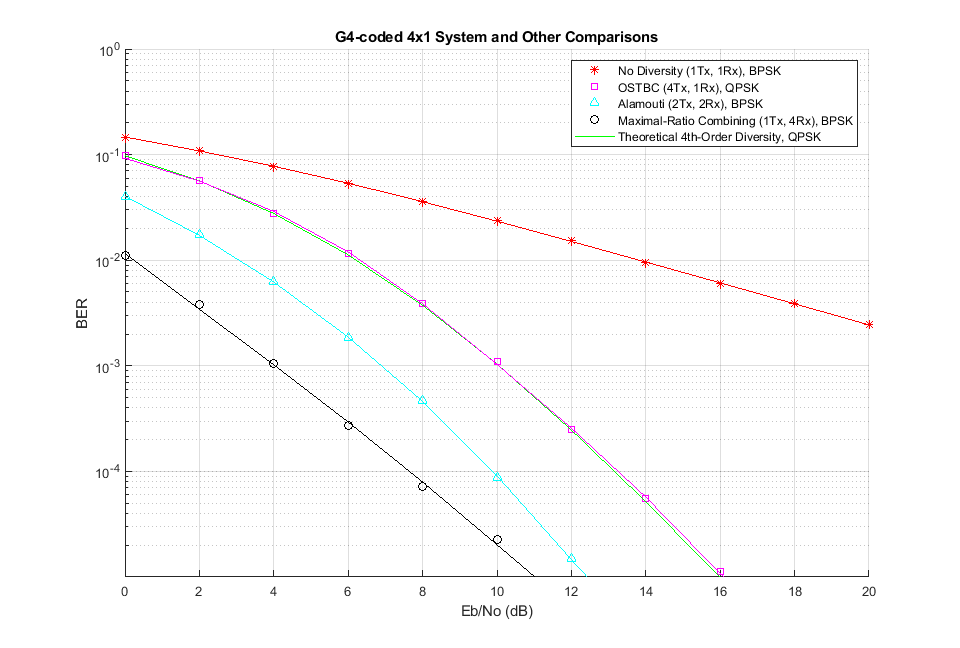
As expected, the similar slopes of the BER curves for the 4x1, 2x2 and 1x4 systems indicate an identical diversity order for each system.
Also observe the 3 dB penalty for the 4x1 system that can be attributed to the same total transmitted power assumption made for each of the three systems. If we calibrate the transmitted power such that the received power for each of these systems is the same, then the three systems would perform identically. Again, the theoretical performance matches the simulation performance of the 4x1 system as the total power is normalized across the diversity branches.
Appendix
This example uses the following helper functions:
References
S. M. Alamouti, "A simple transmit diversity technique for wireless communications", IEEE® Journal on Selected Areas in Communications, Vol. 16, No. 8, Oct. 1998, pp. 1451-1458.
V. Tarokh, H. Jafarkhami, and A.R. Calderbank, "Space-time block codes from orthogonal designs", IEEE Transactions on Information Theory, Vol. 45, No. 5, Jul. 1999, pp. 1456-1467.
A.F. Naguib, V. Tarokh, N. Seshadri, and A.R. Calderbank, "Space-time codes for high data rate wireless communication: Mismatch analysis", Proceedings of IEEE International Conf. on Communications, pp. 309-313, June 1997.
V. Tarokh, H. Jafarkhami, and A.R. Calderbank, "Space-time block codes for wireless communications: Performance results", IEEE Journal on Selected Areas in Communications, Vol. 17, No. 3, Mar. 1999, pp. 451-460.
