place
Pole placement design
Description
Pole placement is a method of calculating the optimum gain matrix used to assign closed-loop poles to specified locations, thereby ensuring system stability. Closed-loop pole locations have a direct impact on time response characteristics such as rise time, settling time, and transient oscillations. For more information, see Pole Placement.
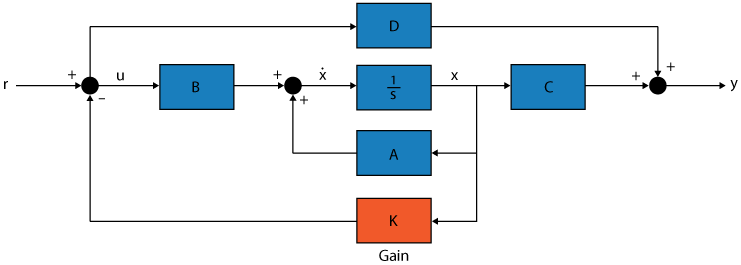
From the figure, consider a linear dynamic system in state-space form
For a given vector p of desired self-conjugate
closed-loop pole locations, place computes a gain matrix
K such that the state feedback u =
–Kx places the poles at the locations p. In other
words, the eigenvalues of A – BK will match the entries
of p (up to the ordering).
K = place(A,B,p)p by computing a state-feedback gain
matrix K. All the inputs of the plant are assumed to be control inputs.
place also works for multi-input systems and is based on the algorithm
from [1]. This algorithm uses
the extra degrees of freedom to find a solution that minimizes the sensitivity of the
closed-loop poles to perturbations in A or B.
[
also returns K,prec] = place(A,B,p)prec, an accuracy estimate of how closely the eigenvalues of
A – BK match the specified locations
p (prec measures the number of accurate decimal
digits in the actual closed-loop poles). A warning is issued if some nonzero closed-loop
pole is more than 10% off from the desired location.
Examples
Input Arguments
Output Arguments
Tips
You can use
placefor estimator gain selection by transposing theAmatrix and substitutingC'for matrixBas follows, as shown in Pole Placement Observer Design. You can use the resultant estimator gain for state estimator workflows usingestim.
References
[1] Kautsky, J., N.K. Nichols, and P. Van Dooren, "Robust Pole Assignment in Linear State Feedback," International Journal of Control, 41 (1985), pp. 1129-1155.
[2] Laub, A.J. and M. Wette, Algorithms and Software for Pole Assignment and Observers, UCRL-15646 Rev. 1, EE Dept., Univ. of Calif., Santa Barbara, CA, Sept. 1984.
Version History
Introduced before R2006a