TuningGoal.Transient
Transient matching requirement for control system tuning
Description
Use the TuningGoal.Transient object to
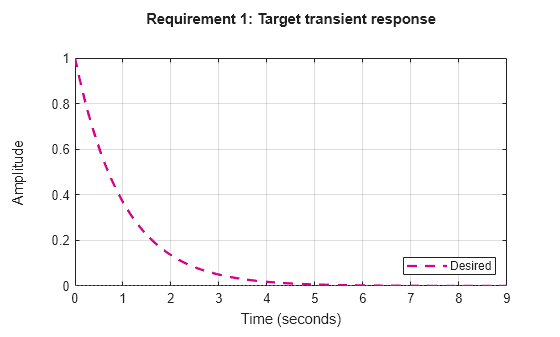
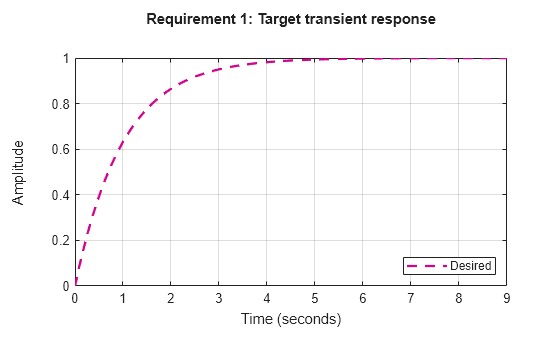
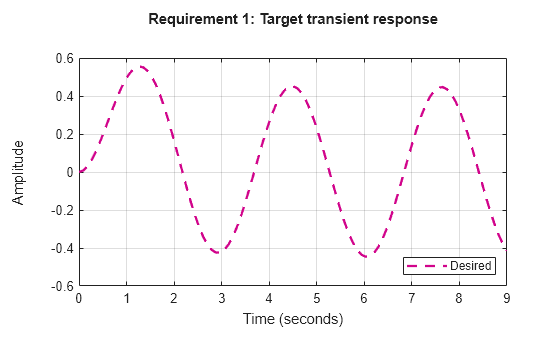
constrain the transient response from specified inputs to specified outputs. This tuning
goal specifies that the transient response closely match the response of a reference
model. Specify the closeness of the required match using the RelGap
property of the tuning goal (see Properties). You can constrain the response to an
impulse, step, or ramp input signal. You can also constrain the response to an input
signal given by the impulse response of an input filter you specify.
Creation
Syntax
Description
Req = TuningGoal.Transient(inputname,outputname,refsys)inputname to
outputname closely matches the impulse response of
the reference model refsys. Specify the closeness of
the required match using the RelGap property of the
tuning goal (see Properties).
inputname and outputname can
describe a SISO or MIMO response of your control system. For MIMO responses,
the number of inputs must equal the number of outputs.
Req = TuningGoal.Transient(inputname,outputname,refsys,inputtype)
Req = TuningGoal.Transient(inputname,outputname,refsys,inputfilter)inputfilter, that is the Laplace transform of
the desired time-domain input signal. The impulse response of
inputfilter is the desired input signal.
Input Arguments
Properties
Examples
Tips
When you use this tuning goal to tune a continuous-time control system,
systuneattempts to enforce zero feedthrough (D = 0) on the transfer that the tuning goal constrains. Zero feedthrough is imposed because the H2 norm, and therefore the value of the tuning goal (see Algorithms), is infinite for continuous-time systems with nonzero feedthrough.systuneenforces zero feedthrough by fixing to zero all tunable parameters that contribute to the feedthrough term.systunereturns an error when fixing these tunable parameters is insufficient to enforce zero feedthrough. In such cases, you must modify the tuning goal or the control structure, or manually fix some tunable parameters of your system to values that eliminate the feedthrough term.When the constrained transfer function has several tunable blocks in series, the software’s approach of zeroing all parameters that contribute to the overall feedthrough might be conservative. In that case, it is sufficient to zero the feedthrough term of one of the blocks. If you want to control which block has feedthrough fixed to zero, you can manually fix the feedthrough of the tuned block of your choice.
To fix parameters of tunable blocks to specified values, use the
ValueandFreeproperties of the block parametrization. For example, consider a tuned state-space block:C = tunableSS('C',1,2,3);To enforce zero feedthrough on this block, set its D matrix value to zero, and fix the parameter.
C.D.Value = 0; C.D.Free = false;
For more information on fixing parameter values, see the Control Design Block reference pages, such as
tunableSS.This tuning goal imposes an implicit stability constraint on the closed-loop transfer function from
InputtoOutput, evaluated with loops opened at the points identified inOpenings. The dynamics affected by this implicit constraint are the stabilized dynamics for this tuning goal. TheMinDecayandMaxRadiusoptions ofsystuneOptionscontrol the bounds on these implicitly constrained dynamics. If the optimization fails to meet the default bounds, or if the default bounds conflict with other requirements, usesystuneOptionsto change these defaults.
Algorithms
When you tune a control system using a TuningGoal, the software
converts the tuning goal into a normalized scalar value
f(x), where x is the vector
of free (tunable) parameters in the control system. The software then adjusts the
parameter values to minimize f(x) or to drive
f(x) below 1 if the tuning goal is a hard
constraint.
For TuningGoal.Transient,
f(x) is based upon the relative gap between the
tuned response and the target response:
y(t) – yref(t) is the response mismatch, and 1 – yref(tr)(t) is the transient portion of yref (deviation from steady-state value or trajectory). denotes the signal energy (2-norm). The gap can be understood as the ratio of the root-mean-square (RMS) of the mismatch to the RMS of the reference transient
Version History
Introduced in R2016aSee Also
looptune | systune | systune (for slTuner) (Simulink Control Design) | looptune (for slTuner) (Simulink Control Design) | viewGoal | evalGoal | TuningGoal.StepTracking | TuningGoal.StepRejection | slTuner (Simulink Control Design)