Multi-Loop Control System
This example shows how to build an arbitrary block diagram by connecting models using
connect. The system is a Smith
Predictor, the single-input, single-output (SISO) multi-loop control system shown in the
following block diagram.
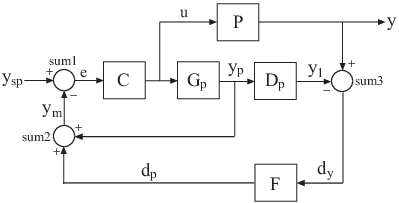
For more information about the Smith Predictor, see Control of Processes with Long Dead Time: The Smith Predictor.
The connect command lets you construct the
overall transfer function from ysp to
y. To use connect, specify the input and
output channel names of the components of the block diagram. connect
automatically joins ports that have the same name, as shown in the following figure.

To build the closed loop model of the Smith Predictor system from ysp to y:
Create the components of the block diagram: the process model
P, the predictor modelGp, the delay modelDp, the filterF, and the PI controllerC. Specify names for the input and output channels of each model so thatconnectcan automatically join them to build the block diagram.s = tf('s'); P = exp(-93.9*s) * 5.6/(40.2*s+1); P.InputName = 'u'; P.OutputName = 'y'; Gp = 5.6/(40.2*s+1); Gp.InputName = 'u'; Gp.OutputName = 'yp'; Dp = exp(-93.9*s); Dp.InputName = 'yp'; Dp.OutputName = 'y1'; F = 1/(20*s+1); F.InputName = 'dy'; F.OutputName = 'dp'; C = pidstd(0.574,40.1); C.Inputname = 'e'; C.OutputName = 'u';Create the summing junctions needed to complete the block diagram.
sum1 = sumblk('e = ysp - ym'); sum2 = sumblk('ym = yp + dp'); sum3 = sumblk('dy = y - y1');The argument to
sumblkis a formula that relates the input and output signals of the summing junction.sumblkcreates a summing junction with the input and output signal names specified in the formula. For example, insum1, the formula'e = ysp - ym'specifies an output signal namede, which is the difference between input signals namedyspandym.Assemble the complete model from ysp to y.
T = connect(P,Gp,Dp,C,F,sum1,sum2,sum3,'ysp','y');
You can list the models and summing junctions in any order because
connectautomatically interconnects them using their input and output channel names.The last two arguments specify the input and output signals of the multi-loop control structure. Thus,
Tis assmodel with inputyspand outputy.