Fit Gaussian Models
About Gaussian Models
The Gaussian model fits peaks, and is given by
where a is the amplitude, b is the centroid (location), c is related to the peak width, n is the number of peaks to fit, and 1 ≤ n ≤ 8.
Gaussian peaks are encountered in many areas of science and engineering. For example, Gaussian peaks can describe line emission spectra and chemical concentration assays.
Fit Gaussian Models Interactively
Open the Curve Fitter app by entering
curveFitterat the MATLAB® command line. Alternatively, on the Apps tab, in the Math, Statistics and Optimization group, click Curve Fitter.In the Curve Fitter app, select curve data. On the Curve Fitter tab, in the Data section, click Select Data. In the Select Fitting Data dialog box, select X data and Y data, or just Y data against an index.
Click the arrow in the Fit Type section to open the gallery, and click Gaussian in the Regression Models group.
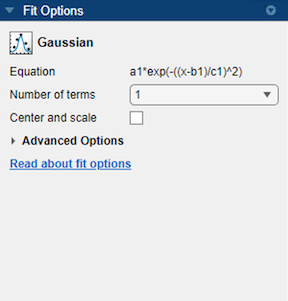
You can specify the following options in the Fit Options pane:
Specify the number of terms as a positive integer in the range [1 8]. Look in the Results pane to see the model terms, values of the coefficients, and goodness-of-fit statistics.
Optionally, in the Advanced Options section, specify coefficient starting values and constraint bounds, or change algorithm settings. The app calculates optimized start points for Gaussian fits, based on the data set. You can override the start points and specify your own values in the Fit Options pane.
Gaussian fits have the width parameter
c1constrained with a lower bound of0. The default lower bounds for most library models are-Inf, which indicates that the coefficients are unconstrained.
For more information on the settings, see Coefficient Constraints: Specify Bounds and Optimized Start Points.
Fit Gaussian Models Using the fit Function
This example shows how to use the fit function to fit a Gaussian model to data.
The Gaussian library model is an input argument to the fit and fittype functions. Specify the model type gauss followed by the number of terms, e.g., 'gauss1' through 'gauss8'.
Fit a Two-Term Gaussian Model
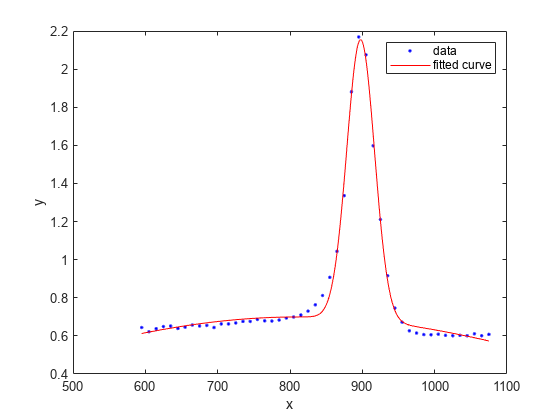
Load some data and fit a two-term Gaussian model.
[x,y] = titanium;
f = fit(x.',y.','gauss2')f =
General model Gauss2:
f(x) = a1*exp(-((x-b1)/c1)^2) + a2*exp(-((x-b2)/c2)^2)
Coefficients (with 95% confidence bounds):
a1 = 1.47 (1.426, 1.515)
b1 = 897.7 (897, 898.3)
c1 = 27.08 (26.08, 28.08)
a2 = 0.6994 (0.6821, 0.7167)
b2 = 810.8 (790, 831.7)
c2 = 592.9 (500.1, 685.7)
plot(f,x,y)
See Also
Apps
Functions
fit|fittype|fitoptions