Chirp
Generate swept-frequency cosine (chirp) signal
Libraries:
DSP System Toolbox /
Sources
Description
The Chirp block outputs a swept-frequency cosine (chirp) signal with unity amplitude and continuous phase. To specify the desired output chirp signal, you must define its instantaneous frequency function, also known as the output frequency sweep. The frequency sweep can be linear, quadratic, or logarithmic, and repeats once every Sweep time by default. For a description of the algorithms used by the Chirp block, see Algorithms.
Examples
Bidirectional Linear Sweep
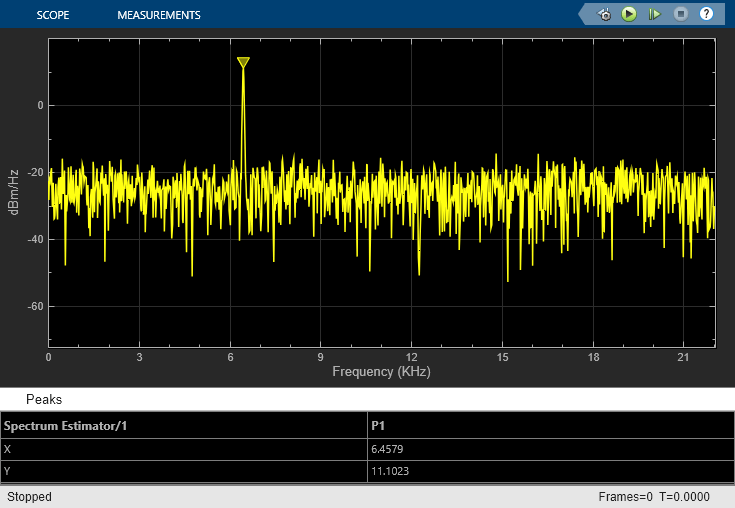
In this example, the Chirp block outputs a bidirectional, linearly swept chirp signal, which is displayed by the Time Scope and the Spectrum Analyzer. You can also export the signal to the MATLAB workspace by the Signal To Workspace block.
To create a bidirectional sweep, set the Sweep mode parameter to Bidirectional. Specify the final frequency of a bidirectional sweep by setting Target time equal to Sweep time, in which case the Target frequency becomes the final frequency in the sweep. Note that in the bidirectional sweep, the period of the sweep is twice the Sweep time of the unidirectional sweep.
Run the model to see the output in the Time Scope and the Spectrum Analyzer.

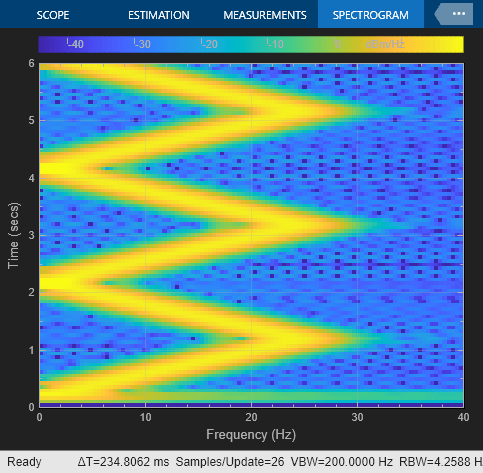
You can also view the spectrogram by saving the output to the workspace and using this command:
spectrogram(dsp_examples_yout,hamming(128),110,0:.01:40,400)

Unidirectional Linear Sweep
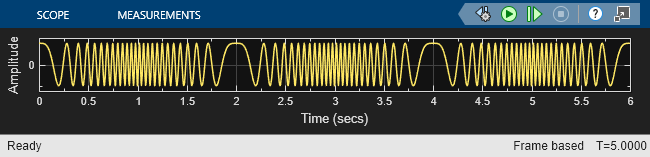
In this example, the Chirp block outputs a unidirectional, linearly swept chirp signal. The Time Scope displays the signal output in the time domain and the Spectrum Analyzer displays the spectrogram in the frequency domain.
To obtain a unidirectional sweep with known initial and final frequency values, in the Chirp block set the Target time equal to Sweep time. In which case, the Target frequency becomes the final frequency in the sweep. Since the Target time is set to equal Sweep time (1 second), the Target frequency (25 Hz) is the final frequency of the unidirectional sweep. This technique might not work for swept cosine sweeps. For details, see the Frequency sweep described for the Frequency sweep parameter.
Run the model to see the time domain output:
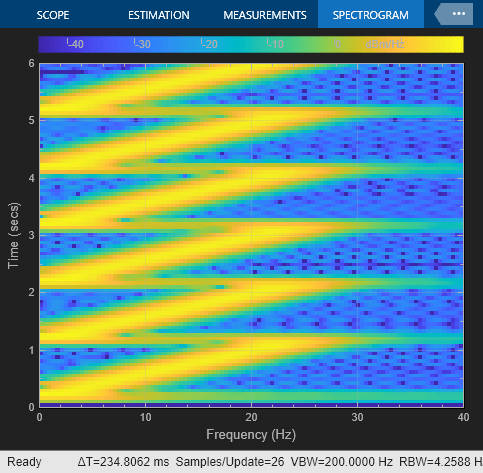
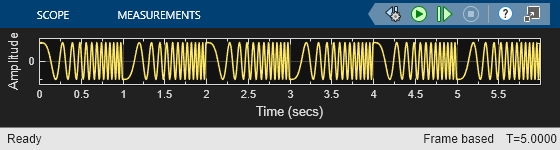
When Sweep Time Is Greater than Target Time
This example shows the unexpected behavior that might arise in the Chirp block when the Sweep time is greater than Target time. The Time Scope displays the signal output, and the Spectrum Analyzer displays the spectrogram in the frequency domain.
Set the Sweep time parameter to 1.5 and specify the final frequency of a bidirectional sweep by setting Target time equal to Sweep time. The sweep reaches the Target frequency (25 Hz) at the Target time (1 second), but since Sweep time is greater than Target time, the sweep continues on its linear path until one Sweep time (1.5 seconds) is traversed.
Unexpected behavior might arise when you set Sweep time greater than Target time.
Run the model to see the chirp signal output and a spectrogram of the frequency domain.



Sweep with Negative Frequencies
In this example, the Chirp block outputs a chirp signal containing negative frequencies. The Time Scope displays the signal output in the time domain, and the Spectrum Analyzer displays the spectrogram in the frequency domain.
Set the Sweep time to 1.5, Initial frequency to 25, Target frequency to 0, and Target time equal to Sweep time. The output chirp of this example might not behave as you expect because the sweep contains negative frequencies between 1 and 1.5 seconds. The sweep reaches the Target frequency (0 Hz) at 1 second, then continues on its negative slope, taking on negative frequency values until it traverses one Sweep time (1.5 seconds).

Run the model to see the time domain output.


Aliased Sweep
In this example, the Chirp block outputs a chirp signal containing negative frequencies. The Time Scope displays the signal output in the time domain, and the Spectrum Analyzer displays the spectrogram in the frequency domain.
Set the Target frequency to 275 and specify Target time equal to Sweep time. The output chirp of this example might not behave as you expect because the sweep contains frequencies greater than half the sampling frequency (200 Hz). If you unexpectedly get a chirp output with a spectrogram resembling the one following, your chirp's sweep might contain frequencies greater than half the sampling frequency.
Run the model to see the signal output and the spectrogram.



Extended Examples
Ports
Output
Port_1 — Swept-frequency cosine (chirp) signal
scalar | vector
Swept-frequency cosine (chirp) signal. In
Linear,
Logarithmic, and
Quadratic modes (set by the
Frequency sweep parameter), the block outputs a
swept-frequency cosine with instantaneous frequency values specified by
the frequency and time parameters. In Swept
cosine mode, the block outputs a swept-frequency
cosine with a linear instantaneous output frequency that may differ from
the one specified by the frequency and time parameters.
For more information about how the block computes the output, see Algorithms.
Data Types: single | double
Parameters
Frequency sweep — Type of frequency sweep
Linear (default) | Swept cosine | Logarithmic | Quadratic
The type of output instantaneous frequency sweep,
fi(t):
Linear,
Logarithmic,
Quadratic, or Swept
cosine. For more information, see Shaping the Frequency Sweep and Algorithms.
Limitations
When you want a linearly swept chirp signal, we recommend that you use
a Linear frequency sweep. Though a
Swept cosine frequency sweep also yields
a linearly swept chirp signal, the output might have unexpected
frequency content.
The swept cosine sweep value at the Target time is not necessarily the Target frequency. This is because the user-specified sweep is not the actual frequency sweep of the swept cosine output, as noted in Output Computation Method for Swept Cosine Frequency Sweep. See the table Instantaneous Frequency Sweep Values for the actual value of the swept cosine sweep at the Target time.
In Swept cosine mode, do not set the parameters so that 1/Tsw is much greater than the values of the Initial frequency and Target frequency parameters. In such cases, the actual frequency content of the swept cosine sweep might be closer to 1/Tsw, far exceeding the Initial frequency and Target frequency parameter values.
Sweep mode — Sweep mode
Unidirectional (default) | Bidirectional
The Sweep mode parameter determines whether your sweep is unidirectional or bidirectional, which affects the shape of your output frequency sweep (see Shaping the Frequency Sweep). The following table describes the characteristics of unidirectional and bidirectional sweeps.
| Sweep Mode Parameter Settings | Sweep Characteristics |
|---|---|
|
|
|
|
The following diagram illustrates a linear sweep in both sweep modes. For information on setting the frequency values in your sweep, see Setting Instantaneous Frequency Sweep Values.

Initial frequency (Hz) — Initial frequency
1000 (default) | scalar
For Linear,
Quadratic, and Swept
cosine sweeps, the initial frequency,
f0, of the output chirp
signal. You can specify the Initial frequency (Hz) as a
scalar, greater than or equal to zero. For
Logarithmic sweeps, Initial
frequency is one less than the actual initial frequency of
the sweep. Also, when the sweep is Logarithmic,
you must set the Initial frequency to be less than the
Target frequency.
For more information, see Setting Instantaneous Frequency Sweep Values.
Tunable: Yes
Target frequency (Hz) — Target frequency
4000 (default) | scalar
For Linear,
Quadratic, and
Logarithmic sweeps, the instantaneous
frequency,
fi(tg),
of the output at the Target time,
tg. You can specify the
Target frequency (Hz) as a scalar, greater than or
equal to zero. For a Swept cosine sweep,
Target frequency is the instantaneous frequency of
the output at half the Target time,
tg/2. When
Frequency sweep is
Logarithmic, you must set the
Target frequency to be greater than the
Initial frequency.
For more information, see Setting Instantaneous Frequency Sweep Values.
Tunable: Yes
Target time (s) — Target time of sweep
1 (default) | scalar
For Linear, Quadratic, and
Logarithmic sweeps, the time,
tg, at which the sweep
reaches the Target frequency,
fi(tg).
For a Swept cosine sweep, Target
time is the time at which the sweep reaches
2fi(tg)
- f0. Target
time must be a scalar that is greater than or equal to zero,
and less than or equal to Sweep time , .
For more information, see Setting Instantaneous Frequency Sweep Values.
Tunable: Yes
Sweep time (s) — Sweep time
1 (default) | scalar
In Unidirectional Sweep
mode, the Sweep time,
Tsw, is the period of the
output frequency sweep. In
Bidirectional Sweep
mode, the Sweep time is half the period of
the output frequency sweep. Sweep time must be a scalar
that is greater than or equal to Target time, .
Tunable: Yes
Initial phase (rad) — Initial phase of cosine output
0 (default) | scalar
The phase, , of the cosine output at t=0; . You can specify the Initial phase (rad) as a scalar that is greater than or equal to zero.
Tunable: Yes
Sample time — Output sample period
1/8000 (default) | positive scalar
The sample period, Ts, of the output. The output frame period is MoTs, where Mo is the number of samples per frame.
Samples per frame — Samples per frame
1 (default) | positive integer
The number of samples, Mo, to buffer into each output frame, specified as a positive integer scalar.
Output data type — Output data type
Double (default) | Single
The data type of the output, specified as single precision or double precision.
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
More About
Shaping the Frequency Sweep
You control the basic shape of the output instantaneous frequency sweep, fi(t), using the Frequency sweep and Sweep mode parameters.
| Parameters for Setting Sweep Shape | Possible Setting | Parameter Description |
|---|---|---|
Frequency sweep | Linear Quadratic Logarithmic Swept cosine | Determines whether the sweep frequencies vary linearly, quadratically, or logarithmically. Linear and swept cosine sweeps both vary linearly. |
Sweep mode | Unidirectional Bidirectional | Determines whether the sweep is unidirectional or bidirectional. For details, see Sweep mode |
The following diagram illustrates the possible shapes of the frequency sweep that you can obtain by setting the Frequency sweep and Sweep mode parameters.

For information on how to set the frequency values in your sweep, see Setting Instantaneous Frequency Sweep Values.
Setting Instantaneous Frequency Sweep Values
Set the following parameters to tune the frequency values of your output frequency sweep.
Initial frequency (Hz), f0
Target frequency (Hz), fi(tg)
Target time (seconds), tg
The following table summarizes the sweep values at specific times for all Frequency sweep settings. For information on the formulas used to compute sweep values at other times, see Algorithms.
Instantaneous Frequency Sweep Values
| Frequency Sweep | Sweep Value at t = 0 | Sweep Value at t = t g | Time When Sweep Value Is Target Frequency, f i ( t g ) |
|---|---|---|---|
Linear | f0 | fi(tg) | tg |
Quadratic | f0 | fi(tg) | tg |
Logarithmic | f0 | fi(tg) | tg |
Swept cosine | f0 | 2fi(tg) - f0 | tg/2 |
Algorithms
The Chirp block uses one of two formulas to compute the block output, depending on the Frequency Sweep parameter setting. For details, see the following sections.
Equations for Output Computation
The following table shows the equations used by the block to compute the
user-specified output frequency sweep,
fi(t), the block
output, ychirp(t), and
the actual output frequency sweep,
fi(actual)(t). The
only time the user-specified sweep is not the actual output sweep is when the
Frequency sweep parameter is set to Swept
cosine.
Note
The following equations apply only to unidirectional sweeps in which fi(0) < fi(tg). To derive equations for other cases, examine the following table and the diagram in Shaping the Frequency Sweep.
The table of equations used by the block contains the following variables:
fi(t) — the user-specified frequency sweep
fi(actual)(t) — the actual output frequency sweep, usually equal to fi(t)
y(t) — the Chirp block output
— the phase of the chirp signal, where , and is the derivative of the phase
— the Initial phase parameter value, where
Equations for Unidirectional Positive Sweeps
| Frequency Sweep | Block Output Chirp Signal | User-Specified Frequency Sweep, f i ( t ) | Actual Frequency Sweep, f i(actual) ( t ) | |
|---|---|---|---|---|
| ||||
| Same as | |||
| Same as | Where fi(tg) > f0> 0 | N/A | |
| Same as | Same as |
Output Computation Method for Linear, Quadratic, and Logarithmic Frequency Sweeps
The derivative of the phase of a chirp function gives the instantaneous frequency
of the chirp function. The Chirp block uses this principle to
calculate the chirp output when the Frequency Sweep parameter
is set to Linear, Quadratic,
or Logarithmic.
Linear, quadratic, or logarithmic chirp signal with phase | |
Phase derivative is instantaneous frequency |
For instance, if you want a chirp signal with a linear instantaneous frequency
sweep, set the Frequency Sweep parameter to
Linear, and tune the linear sweep values by setting
other parameters appropriately. The block outputs a chirp signal, the phase
derivative of which is the specified linear sweep. This ensures that the
instantaneous frequency of the output is the linear sweep you desired. For equations
describing the linear, quadratic, and logarithmic sweeps, see Equations for Output Computation.
Output Computation Method for Swept Cosine Frequency Sweep
To generate the swept cosine chirp signal, the block sets the swept cosine chirp output as follows.
Swept cosine chirp output (Instantaneous frequency equation, does not hold.) |
The instantaneous frequency equation, shown in Output Computation Method for Linear, Quadratic, and Logarithmic Frequency Sweeps, does not hold for the swept cosine chirp, so the user-defined frequency sweep, fi(t), is not the actual output frequency sweep, fi(actual)(t), of the swept cosine chirp. Thus, the swept cosine output might not behave as you expect. To learn more about swept cosine chirp behavior, see Frequency sweep described for the Frequency sweep parameter and Equations for Output Computation.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)