Assess EGARCH Forecast Bias Using Simulations
This example shows how to simulate an EGARCH process. Simulation-based forecasts are compared to minimum mean square error (MMSE) forecasts, showing the bias in MMSE forecasting of EGARCH processes.
Specify an EGARCH model.
Specify an EGARCH(1,1) process with constant , GARCH coefficient , ARCH coefficient and leverage coefficient .
Mdl = egarch('Constant',0.01,'GARCH',0.7,... 'ARCH',0.3,'Leverage',-0.1)
Mdl =
egarch with properties:
Description: "EGARCH(1,1) Conditional Variance Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 1
Q: 1
Constant: 0.01
GARCH: {0.7} at lag [1]
ARCH: {0.3} at lag [1]
Leverage: {-0.1} at lag [1]
Offset: 0
Simulate one realization.
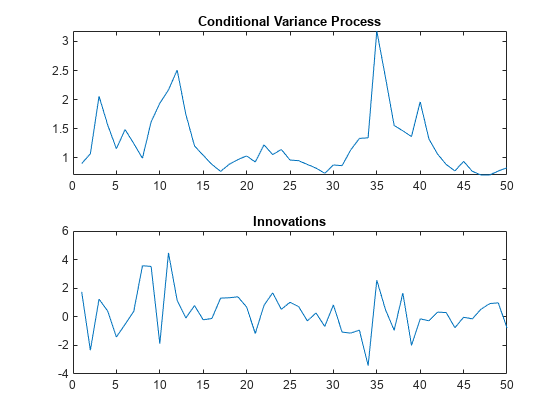
Simulate one realization of length 50 from the EGARCH conditional variance process and corresponding innovations.
rng default; % For reproducibility [v,y] = simulate(Mdl,50); figure subplot(2,1,1) plot(v) xlim([0,50]) title('Conditional Variance Process') subplot(2,1,2) plot(y) xlim([0,50]) title('Innovations')
Simulate multiple realizations.
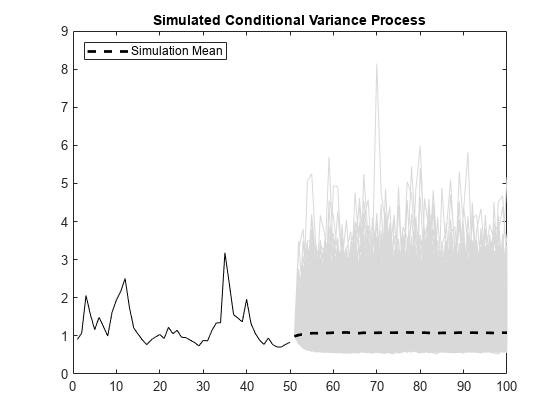
Using the generated conditional variances and innovations as presample data, simulate 5000 realizations of the EGARCH process for 50 future time steps. Plot the simulation mean of the forecasted conditional variance process.
rng default; % For reproducibility [Vsim,Ysim] = simulate(Mdl,50,'NumPaths',5000,... 'E0',y,'V0',v); figure plot(v,'k') hold on plot(51:100,Vsim,'Color',[.85,.85,.85]) xlim([0,100]) h = plot(51:100,mean(Vsim,2),'k--','LineWidth',2); title('Simulated Conditional Variance Process') legend(h,'Simulation Mean','Location','NorthWest') hold off
Compare simulated and MMSE conditional variance forecasts.
Compare the simulation mean variance, the MMSE variance forecast, and the exponentiated, theoretical unconditional log variance.
The exponentiated, theoretical unconditional log variance for the specified EGARCH(1,1) model is
sim = mean(Vsim,2); fcast = forecast(Mdl,50,y,'V0',v); sig2 = exp(0.01/(1-0.7)); figure plot(sim,':','LineWidth',2) hold on plot(fcast,'r','LineWidth',2) plot(ones(50,1)*sig2,'k--','LineWidth',1.5) legend('Simulated','MMSE','Theoretical') title('Unconditional Variance Comparisons') hold off
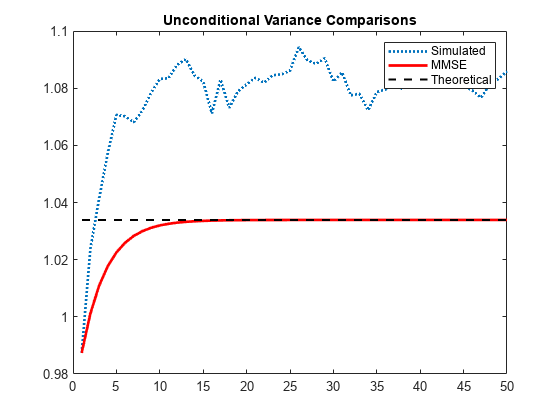
The MMSE and exponentiated, theoretical log variance are biased relative to the unconditional variance (by about 4%) because by Jensen's inequality,
Compare simulated and MMSE log conditional variance forecasts.
Compare the simulation mean log variance, the log MMSE variance forecast, and the theoretical, unconditional log variance.
logsim = mean(log(Vsim),2); logsig2 = 0.01/(1-0.7); figure plot(logsim,':','LineWidth',2) hold on plot(log(fcast),'r','LineWidth',2) plot(ones(50,1)*logsig2,'k--','LineWidth',1.5) legend('Simulated','MMSE','Theoretical') title('Unconditional Log Variance Comparisons') hold off
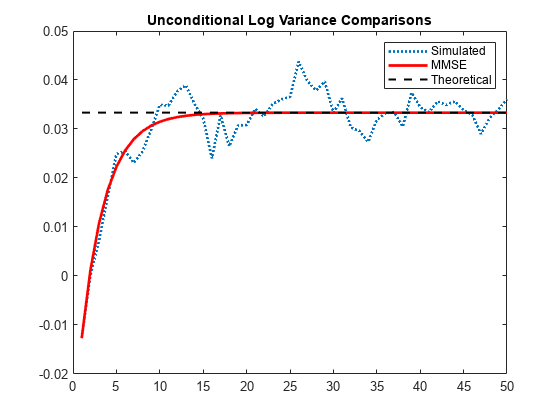
The MMSE forecast of the unconditional log variance is unbiased.