Filter States of State-Space Model
This example shows how to filter states of a known, time-invariant, state-space model.
Suppose that a latent process is an AR(1). The state equation is
where is Gaussian with mean 0 and standard deviation 1.
Generate a random series of 100 observations from , assuming that the series starts at 1.5.
T = 100; ARMdl = arima('AR',0.5,'Constant',0,'Variance',1); x0 = 1.5; rng(1); % For reproducibility x = simulate(ARMdl,T,'Y0',x0);
Suppose further that the latent process is subject to additive measurement error. The observation equation is
where is Gaussian with mean 0 and standard deviation 0.75. Together, the latent process and observation equations compose a state-space model.
Use the random latent state process (x) and the observation equation to generate observations.
y = x + 0.75*randn(T,1);
Specify the four coefficient matrices.
A = 0.5; B = 1; C = 1; D = 0.75;
Specify the state-space model using the coefficient matrices.
Mdl = ssm(A,B,C,D)
Mdl =
State-space model type: ssm
State vector length: 1
Observation vector length: 1
State disturbance vector length: 1
Observation innovation vector length: 1
Sample size supported by model: Unlimited
State variables: x1, x2,...
State disturbances: u1, u2,...
Observation series: y1, y2,...
Observation innovations: e1, e2,...
State equation:
x1(t) = (0.50)x1(t-1) + u1(t)
Observation equation:
y1(t) = x1(t) + (0.75)e1(t)
Initial state distribution:
Initial state means
x1
0
Initial state covariance matrix
x1
x1 1.33
State types
x1
Stationary
Mdl is an ssm model. Verify that the model is correctly specified using the display in the Command Window. The software infers that the state process is stationary. Subsequently, the software sets the initial state mean and covariance to the mean and variance of the stationary distribution of an AR(1) model.
Estimate the filtered states for periods 1 through 100. Plot the true state values and the estimated, filtered states.
filteredX = filter(Mdl,y); figure plot(1:T,x,'-k',1:T,filteredX,':r','LineWidth',2) title({'State Values'}) xlabel('Period') ylabel('State') legend({'True state values','Filtered state values'})
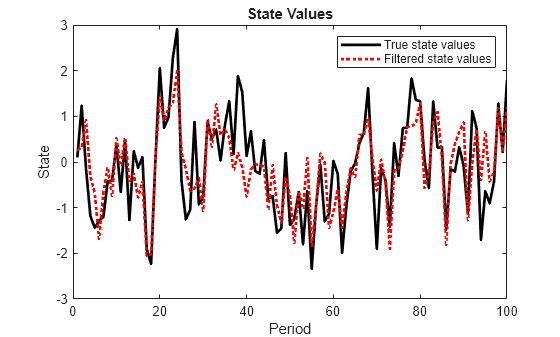
The true values and filter estimates are approximately the same.
See Also
ssm | estimate | filter | smooth
