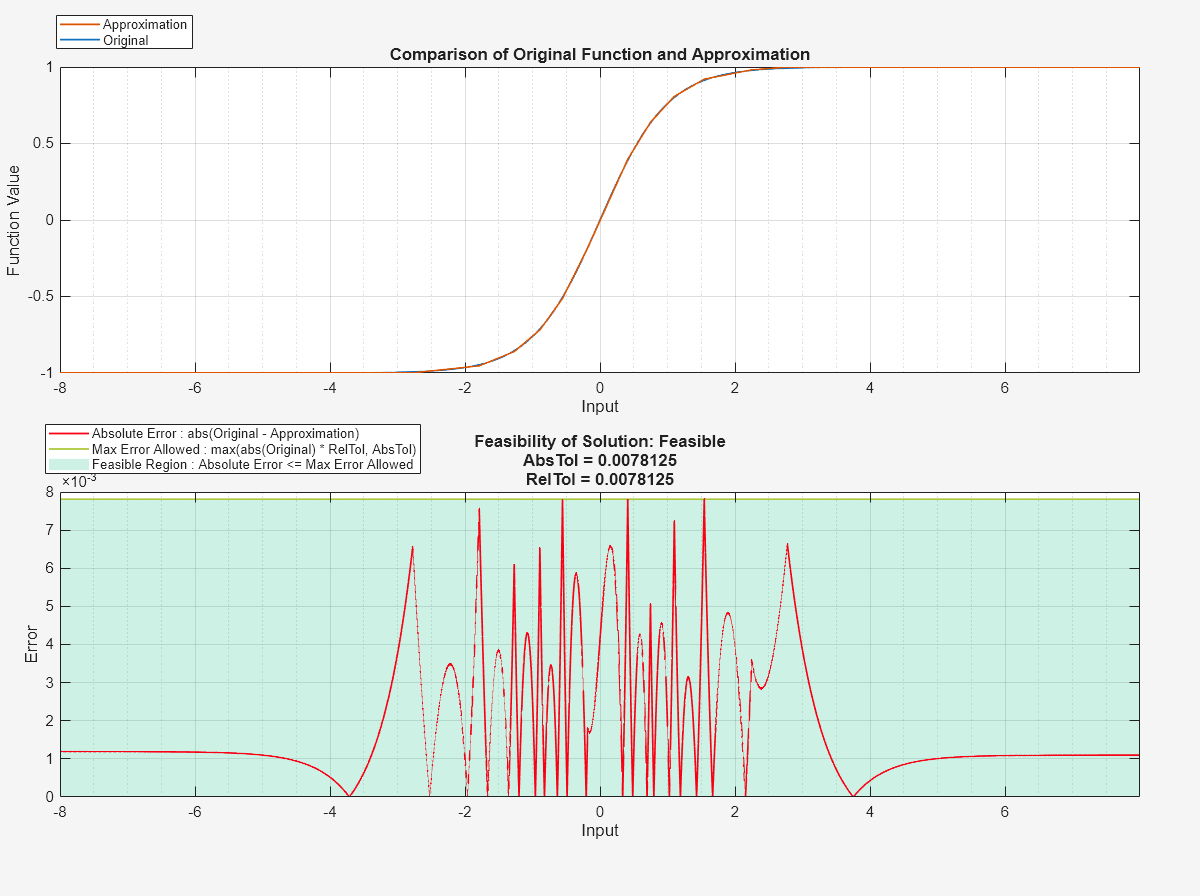
compare
Class: FunctionApproximation.LUTSolution
Namespace: FunctionApproximation
Compare numerical results of
FunctionApproximation.LUTSolution to original function or lookup
table
Syntax
data = compare(solution)
Description
data = compare(solution)FunctionApproximation.LUTSolution object, solution,
and the original lookup table, function, or Math Function block.
Input Arguments
Output Arguments
Examples
Version History
Introduced in R2018a
See Also
Apps
Classes
FunctionApproximation.Problem|FunctionApproximation.Options|FunctionApproximation.LUTSolution|FunctionApproximation.LUTMemoryUsageCalculator