Calculate Complex dB Using a Direct Lookup Table
You can calculate complex decibel levels using the following formula.
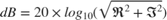
However, this equation contains expressions, such as the log calculation, that are not efficient to implement on hardware. Using a direct lookup table, you can very closely approximate this expression in a way that is efficient on hardware.
To begin, define the function to approximate with a lookup table.
f = @(re,im) 20*log10(sqrt(re.^2 + im.^2));
To specify the tolerances that are acceptable, and the desired word lengths to use in the lookup table, use the FunctionApproximation.Options object. To generate a direct lookup table, set the Interpolation property of the Options object to None. Use the ApproximateSolutionType property to specify whether to return the lookup table as a Simulink® subsystem or as a MATLAB® function.
options = FunctionApproximation.Options('Interpolation', 'None', 'AbsTol', 0.25, 'RelTol', 0, 'WordLengths', 5:10, 'ApproximateSolutionType', 'Simulink'); % Problem setup problem = FunctionApproximation.Problem(f, 'Options', options); problem.InputTypes = [numerictype(0,5,0) numerictype(0,5,0)]; problem.InputLowerBounds = [1 1]; problem.InputUpperBounds = [Inf Inf]; % upper bound will clip to input types range problem.OutputType = numerictype(0,10,4);
The solve function returns the optimal lookup table as a FunctionApproximation.LUTSolution object. As the software optimizes the parameters of the lookup table, MATLAB displays information about each iteration of the optimization, including the total memory used by the lookup table, the word lengths used for data in the lookup table, and the maximum difference in output between the original function and the lookup table approximation. The best solution is defined as the lookup table using the smallest memory that meets the tolerances and other constraints defined in the Options object.
solution = solve(problem)
Maximum for input 2 has been set to the maximum representable value of the type numerictype(0,5,0) = 31.
Maximum for input 1 has been set to the maximum representable value of the type numerictype(0,5,0) = 31.
| ID | Memory (bits) | Feasible | Table Size | Intermediate WLs | TableData WL | Error(Max,Current) |
| 0 | 10240 | 1 | [32 32] | [5 5] | 10 | 2.500000e-01, 3.119254e-02 |
| 1 | 9216 | 1 | [32 32] | [5 5] | 9 | 2.500000e-01, 6.228219e-02 |
| 2 | 8192 | 1 | [32 32] | [5 5] | 8 | 2.500000e-01, 1.248211e-01 |
| 3 | 7168 | 1 | [32 32] | [5 5] | 7 | 2.500000e-01, 2.481815e-01 |
Best Solution
| ID | Memory (bits) | Feasible | Table Size | Intermediate WLs | TableData WL | Error(Max,Current) |
| 3 | 7168 | 1 | [32 32] | [5 5] | 7 | 2.500000e-01, 2.481815e-01 |
solution =
1×1 FunctionApproximation.LUTSolution with properties:
ID: 3
Feasible: "true"
Compare the output of the original function and the lookup table approximation. The left plot shows the output of the original function defined in the Problem object, and the lookup table approximation. The plot on the right shows the difference between the output of the original function and the corresponding output from the generated lookup table approximation. The difference between the two outputs is less than the tolerance specified in the Options object.
compareData = compare(solution)
compareData =
1×2 struct array with fields:
Breakpoints
Original
Approximate

Access the TableData property of the solution to use the lookup table in a MATLAB application.
tableData = solution.TableData
tableData =
struct with fields:
BreakpointValues: {[1×32 double] [1×32 double]}
BreakpointDataTypes: [2×1 embedded.numerictype]
TableValues: [32×32 double]
TableDataType: [1×1 embedded.numerictype]
IsEvenSpacing: 1
Interpolation: None
Use the approximate function to generate a Simulink subsystem containing the lookup table approximation.
approximate(solution)

You can use the generated subsystem containing the lookup table in an HDL application. To check that the lookup table is compatible with HDL code generation using HDL Coder™, use the checkhdl function.