Design Optimization of a Welded Beam
This example shows how to examine the tradeoff between the strength and cost of a beam. Several publications use this example as a test problem for various multiobjective algorithms, including Deb et al. [1] and Ray and Liew [2].
For a video overview of this example, see Pareto Sets for Multiobjective Optimization.
Problem Description
The following sketch is adapted from Ray and Liew [2].

This sketch represents a beam welded onto a substrate. The beam supports a load P at a distance L from the substrate. The beam is welded onto the substrate with upper and lower welds, each of length l and thickness h. The beam has a rectangular cross-section, width b, and height t. The material of the beam is steel.
The two objectives are the fabrication cost of the beam and the deflection of the end of the beam under the applied load P. The load P is fixed at 6,000 lbs, and the distance L is fixed at 14 in.
The design variables are:
x(1) = h, the thickness of the welds
x(2) = l, the length of the welds
x(3) = t, the height of the beam
x(4) = b, the width of the beam
The fabrication cost of the beam is proportional to the amount of material in the beam, , plus the amount of material in the welds, . Using the proportionality constants from the cited papers, the first objective is
The deflection of the beam is proportional to P and inversely proportional to . Again, using the proportionality constants from the cited papers, the second objective is
, where and .
The problem has several constraints.
The weld thickness cannot exceed the beam width. In symbols, x(1) <= x(4). In toolbox syntax:
Aineq = [1,0,0,-1]; bineq = 0;
The shear stress on the welds cannot exceed 13,600 psi. To calculate the shear stress, first calculate preliminary expressions:
In summary, the shear stress on the welds has the constraint <= 13600.
The normal stress on the welds cannot exceed 30,000 psi. The normal stress is .
The buckling load capacity in the vertical direction must exceed the applied load of 6,000 lbs. Using the values of Young's modulus psi and psi, the buckling load constraint is . Numerically, this becomes the inequality .
The bounds on the variables are 0.125 <=x(1) <= 5, 0.1 <= x(2) <= 10, 0.1 <= x(3) <= 10, and 0.125 <= x(4) <= 5. In toolbox syntax:
lb = [0.125,0.1,0.1,0.125]; ub = [5,10,10,5];
The objective functions appear at the end of this example in the function objval(x). The nonlinear constraints appear at the end of this example in the function nonlcon(x).
Multiobjective Problem Formulation and paretosearch Solution
You can optimize this problem in several ways:
Set a maximum deflection, and find a single-objective minimal fabrication cost over designs that satisfy the maximum deflection constraint.
Set a maximum fabrication cost, and find a single-objective minimal deflection over designs that satisfy the fabrication cost constraint.
Solve a multiobjective problem, visualizing the tradeoff between the two objectives.
To use the multiobjective approach, which gives more information about the problem, set the objective function and nonlinear constraint function.
fun = @objval; nlcon = @nonlcon;
Solve the problem using paretosearch with the 'psplotparetof' plot function. To reduce the amount of diagnostic display information, set the Display option to 'off'.
opts_ps = optimoptions('paretosearch','Display','off','PlotFcn','psplotparetof'); rng default % For reproducibility [x_ps1,fval_ps1,~,psoutput1] = paretosearch(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ps);
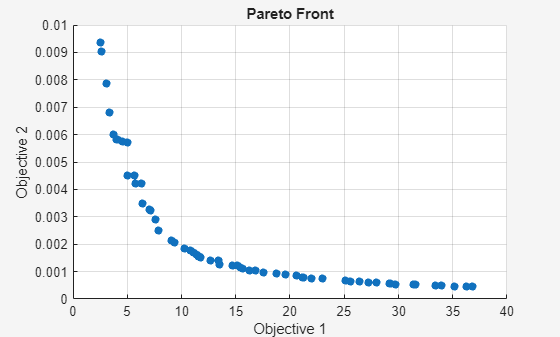
disp("Total Function Count: " + psoutput1.funccount);Total Function Count: 1467
For a smoother Pareto front, try using more points.
npts = 160; % The default is 60
opts_ps.ParetoSetSize = npts;
[x_ps2,fval_ps2,~,psoutput2] = paretosearch(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ps);
disp("Total Function Count: " + psoutput2.funccount);Total Function Count: 4697
This solution looks like a smoother curve. The solver takes over three times as many function evaluations when using 160 Pareto points instead of 60.
gamultiobj Solution
To see if the solver makes a difference, try the gamultiobj solver on the problem. Set equivalent options as in the previous solution. Because the gamultiobj solver keeps fewer than half of its solutions on the best Pareto front, use two times as many points as before.
opts_ga = optimoptions('gamultiobj','Display','off','PlotFcn','gaplotpareto','PopulationSize',2*npts); [x_ga1,fval_ga1,~,gaoutput1] = gamultiobj(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ga);

disp("Total Function Count: " + gaoutput1.funccount);Total Function Count: 44161
gamultiobj takes tens of thousands of function evaluations, whereas paretosearch takes only thousands. gamultiobj has a slightly larger extent of the objective function values, particularly for Objective 2.
Compare Solutions
The gamultiobj solution seems to differ from the paretosearch solution, although it is difficult to tell because the plotted scales differ. Plot the two solutions on the same plot, using the same scale.
fps2 = sortrows(fval_ps2,1,'ascend'); figure hold on plot(fps2(:,1),fps2(:,2),'r-') fga = sortrows(fval_ga1,1,'ascend'); plot(fga(:,1),fga(:,2),'b--') xlim([0,40]) ylim([0,1e-2]) legend('paretosearch','gamultiobj') xlabel 'Cost' ylabel 'Deflection' hold off

The paretosearch solution is better in the leftmost portion of the plot, and for the remainder the solutions look indistinguishable. paretosearch uses many fewer function evaluations to obtain its solution.
Typically, when the problem has no nonlinear constraints, paretosearch is at least as accurate as gamultiobj. However, the resulting Pareto sets can have somewhat different ranges.
One of the main advantages of paretosearch is that it usually takes many fewer function evaluations.
Start from Single-Objective Solutions
To help the solvers find better solutions, start them from points that are the solutions to minimizing the individual objective functions. The pickindex function returns a single objective from the objval function. Use fmincon to find single-objective optima. Then use those solutions as initial points for a multiobjective search.
x0 = zeros(2,4); x0f = (lb + ub)/2; opts_fmc = optimoptions('fmincon','Display','off','MaxFunctionEvaluations',1e4); x0(1,:) = fmincon(@(x)pickindex(x,1),x0f,Aineq,bineq,[],[],lb,ub,@nonlcon,opts_fmc); x0(2,:) = fmincon(@(x)pickindex(x,2),x0f,Aineq,bineq,[],[],lb,ub,@nonlcon,opts_fmc);
Examine the single-objective optima.
objval(x0(1,:))
ans = 1×2
2.3810 0.0158
objval(x0(2,:))
ans = 1×2
76.7188 0.0004
The minimum cost is 2.381, which gives a deflection of 0.158. The minimum deflection is 0.0004, which has a cost of 76.7188. The plotted curves are quite steep near the ends of their ranges, meaning you get much less deflection if you take a cost a bit above its minimum, or much less cost if you take a deflection a bit above its minimum.
Start paretosearch from the single-objective solutions. Because you will plot the solutions later on the same plot, remove the paretosearch plot function.
opts_ps.InitialPoints = x0;
opts_ps.PlotFcn = [];
[x_psx0,fval_ps1x0,~,psoutput1x0] = paretosearch(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ps);
disp("Total Function Count: " + psoutput1x0.funccount);Total Function Count: 4355
Start ga from the same initial points, and remove its plot function.
opts_ga.InitialPopulationMatrix = x0;
opts_ga.PlotFcn = [];
[~,fval_ga,~,gaoutput] = gamultiobj(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ga);
disp("Total Function Count: " + gaoutput.funccount);Total Function Count: 47361
Plot the solutions on the same axes.
fps = sortrows(fval_ps1x0,1,'ascend'); figure hold on plot(fps(:,1),fps(:,2),'r-') fga = sortrows(fval_ga,1,'ascend'); plot(fga(:,1),fga(:,2),'b--') xlim([0,40]) ylim([0,1e-2]) legend('paretosearch','gamultiobj') xlabel 'Cost' ylabel 'Deflection' hold off

By starting from the single-objective solutions, the gamultiobj solution is similar to the paretosearch solution throughout the plotted range. However, gamultiobj takes almost ten times as many function evaluations to reach its solution.
Hybrid Function
gamultiobj can call the hybrid function fgoalattain automatically to attempt to reach a more accurate solution. See whether the hybrid function improves the solution.
opts_ga.HybridFcn = 'fgoalattain'; [xgah,fval_gah,~,gaoutputh] = gamultiobj(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ga); disp("Total Function Count: " + gaoutputh.funccount);
Total Function Count: 47681
fgah = sortrows(fval_gah,1,'ascend'); figure hold on plot(fps(:,1),fps(:,2),'r-') plot(fga(:,1),fga(:,2),'b--') plot(fgah(:,1),fgah(:,2),'g-') xlim([0,40]) ylim([0,1e-2]) legend('paretosearch','gamultiobj','gamultiobj/fgoalattain') xlabel 'Cost' ylabel 'Deflection' hold off
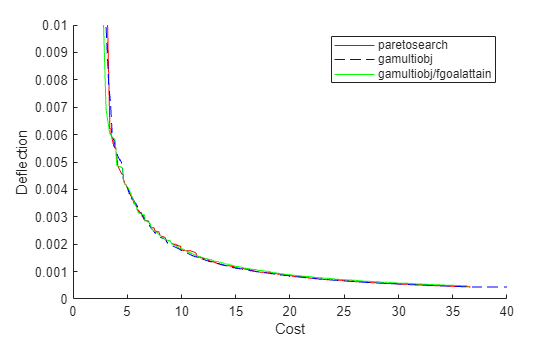
The hybrid function provides a slight improvement on the gamultiobj solution, mainly in the leftmost part of the plot.
Run fgoalattain Manually from paretosearch Solution Points
Although paretosearch has no built-in hybrid function, you can improve the paretosearch solution by running fgoalattain from the paretosearch solution points. Create a goal and weights for fgoalattain by using the same setup for fgoalattain as described in gamultiobj Hybrid Function.
Fmax = max(fval_ps1x0); nobj = numel(Fmax); Fmin = min(fval_ps1x0); w = sum((Fmax - fval_ps1x0)./(1 + Fmax - Fmin),2); p = w.*((Fmax - fval_ps1x0)./(1 + Fmax - Fmin)); xnew = zeros(size(x_psx0)); nsol = size(xnew,1); fvalnew = zeros(nsol,nobj); opts_fg = optimoptions('fgoalattain','Display','off'); nfv = 0; for ii = 1:nsol [xnew(ii,:),fvalnew(ii,:),~,~,output] = fgoalattain(fun,x_psx0(ii,:),fval_ps1x0(ii,:),p(ii,:),... Aineq,bineq,[],[],lb,ub,nlcon,opts_fg); nfv = nfv + output.funcCount; end disp("fgoalattain Function Count: " + nfv)
fgoalattain Function Count: 11940
fnew = sortrows(fvalnew,1,'ascend'); figure hold on plot(fps(:,1),fps(:,2),'r-') plot(fga(:,1),fga(:,2),'b--') plot(fgah(:,1),fgah(:,2),'g-') plot(fnew(:,1),fnew(:,2),'k.-') xlim([0,40]) ylim([0,1e-2]) legend('paretosearch','gamultiobj','gamultiobj/fgoalattain','paretosearch/fgoalattain') xlabel 'Cost' ylabel 'Deflection'

The combination of paretosearch and fgoalattain creates the most accurate Pareto front. Zoom in to see.
xlim([3.64 13.69])
ylim([0.00121 0.00442])
hold off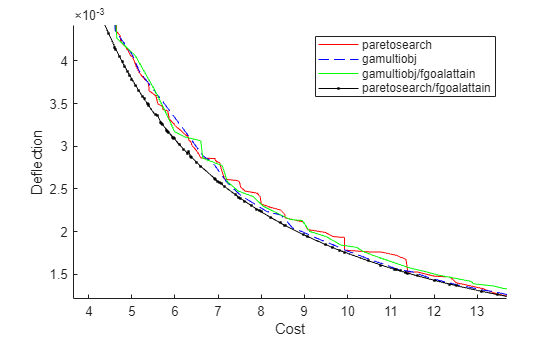
Even with the extra fgoalattain computations, the total function count for the combination is less than half of the function count for the gamultiobj solution alone.
fprintf("Total function count for gamultiobj alone is %d.\n" + ... "For paretosearch and fgoalattain together it is %d.\n",... gaoutput.funccount,nfv + psoutput1x0.funccount)
Total function count for gamultiobj alone is 47361. For paretosearch and fgoalattain together it is 16295.
Find Good Parameters from Plot
The plotted points show the best values in function space. To determine which parameters achieve these function values, find the size of the beam and size of the weld in order to get a particular cost/deflection point. For example, the plot of paretosearch followed by fgoalattain shows points with a cost of about 6 and a deflection of about 3.5e–3. Determine the sizes of the beam and weld that achieve these points.
whichgood = find(fvalnew(:,1) <= 6 & fvalnew(:,2) <= 3.5e-3); goodpoints = table(xnew(whichgood,:),fvalnew(whichgood,:),'VariableNames',{'Parameters' 'Objectives'})
goodpoints=15×2 table
Parameters Objectives
________________________________________ ___________________
0.61638 1.5707 10 0.63173 5.3916 0.0034749
0.63309 1.5228 10 0.66925 5.6722 0.0032801
0.47654 2.124 10 0.65248 5.5943 0.0033644
0.64402 1.4929 10 0.69431 5.8592 0.0031617
0.6513 1.4736 10 0.71125 5.9854 0.0030864
0.64938 1.4787 10 0.70676 5.9519 0.003106
0.61437 1.5767 10 0.62727 5.3582 0.0034996
0.6157 1.5728 10 0.63022 5.3803 0.0034832
0.63478 1.5181 10 0.67309 5.7009 0.0032614
0.64269 1.4965 10 0.69125 5.8364 0.0031757
0.64144 1.4999 10 0.68835 5.8148 0.0031891
0.63509 1.5173 10 0.6738 5.7062 0.0032579
0.65081 1.4749 10 0.71009 5.9768 0.0030914
0.62551 1.5442 10 0.6521 5.5441 0.0033663
0.65034 1.4762 10 0.70899 5.9685 0.0030962
Several sets of parameters achieve a cost of less than 6 and a deflection of less than 3.5e–3:
Weld thickness slightly over 0.6
Weld length about 1.5
Beam height 10 (the upper bound)
Beam width between 0.63 and 0.71
Objective and Nonlinear Constraints
function [Cineq,Ceq] = nonlcon(x) sigma = 5.04e5 ./ (x(:,3).^2 .* x(:,4)); P_c = 64746.022*(1 - 0.028236*x(:,3)).*x(:,3).*x(:,4).^3; tp = 6e3./sqrt(2)./(x(:,1).*x(:,2)); tpp = 6e3./sqrt(2) .* (14+0.5*x(:,2)).*sqrt(0.25*(x(:,2).^2 + (x(:,1) + x(:,3)).^2)) ./ (x(:,1).*x(:,2).*(x(:,2).^2 / 12 + 0.25*(x(:,1) + x(:,3)).^2)); tau = sqrt(tp.^2 + tpp.^2 + (x(:,2).*tp.*tpp)./sqrt(0.25*(x(:,2).^2 + (x(:,1) + x(:,3)).^2))); Cineq = [tau - 13600,sigma - 3e4,6e3 - P_c]; Ceq = []; end function F = objval(x) f1 = 1.10471*x(:,1).^2.*x(:,2) + 0.04811*x(:,3).*x(:,4).*(14.0+x(:,2)); f2 = 2.1952./(x(:,3).^3 .* x(:,4)); F = [f1,f2]; end function z = pickindex(x,k) z = objval(x); % evaluate both objectives z = z(k); % return objective k end
References
[1] Deb, Kalyanmoy, J. Sundar, Udaya Bhaskara Rao N, and Shamik Chaudhuri. Reference Point Based Multi-Objective Optimization Using Evolutionary Algorithms. International Journal of Computational Intelligence Research, Vol. 2, No. 3, 2006, pp. 273–286. Available at https://repository.ias.ac.in/81053/1/17-p.pdf.
[2] Ray, T., and K. M. Liew. A Swarm Metaphor for Multiobjective Design Optimization. Engineering Optimization 34, 2002, pp.141–153.