HDL Code Generation for LMS Filter
This example shows how to generate HDL code from a MATLAB® design that implements an LMS filter. The example also illustrates how to design a test bench that cancels out the noise signal by using this filter.
LMS Filter MATLAB Design
The MATLAB design used in the example is an implementation of an LMS (Least Mean Squares) filter. The LMS filter is a class of adaptive filter that identifies an FIR filter signal that is embedded in the noise. The LMS filter design implementation in MATLAB consists of a top-level function mlhdlc_lms_fcn that calculates the optimal filter coefficients to reduce the difference between the output signal and the desired signal.
design_name = 'mlhdlc_lms_fcn'; testbench_name = 'mlhdlc_lms_noise_canceler_tb';
Review the MATLAB design:
open(design_name);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % MATLAB Design: Adaptive Noise Canceler algorithm using Least Mean Square % (LMS) filter implemented in MATLAB % % Key Design pattern covered in this example: % (1) Use of function calls % (2) Function inlining vs instantiation knobs available in the code % generator % (3) Use of system objects in the testbench to stream test vectors into the design %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %#codegen function [filtered_signal, y, fc] = mlhdlc_lms_fcn(input, ... desired, step_size, reset_weights) % 'input' : The signal from Exterior Mic which records the ambient noise. % 'desired': The signal from Pilot's Mic which includes % original music signal and the noise signal % 'err_sig': The difference between the 'desired' and the filtered 'input' % It represents the estimated music signal (output of this block) % % The LMS filter is trying to retrieve the original music signal('err_sig') % from Pilot's Mic by filtering the Exterior Mic's signal and using it to % cancel the noise in Pilot's Mic. The coefficients/weights of the filter % are updated(adapted) in real-time based on 'input' and 'err_sig'. % register filter coefficients persistent filter_coeff; if isempty(filter_coeff) filter_coeff = zeros(1, 40); end % Variable Filter: Call 'mtapped_delay_fcn' function on path to create % 40-step tapped delay delayed_signal = mtapped_delay_fcn(input); % Apply filter coefficients weight_applied = delayed_signal .* filter_coeff; % Call treesum function on matlab path to sum up the results filtered_signal = mtreesum_fcn(weight_applied); % Output estimated Original Signal td = desired; tf = filtered_signal; esig = td - tf; y = esig; % Update Weights: Call 'update_weight_fcn' function on MATLAB path to % calculate the new weights updated_weight = update_weight_fcn(step_size, esig, delayed_signal, ... filter_coeff, reset_weights); % update filter coefficients register filter_coeff = updated_weight; fc = filter_coeff; function y = mtreesum_fcn(u) %Implement the 'sum' function without a for-loop % y = sum(u); % The loop based implementation of 'sum' function is not ideal for % HDL generation and results in a longer critical path. % A tree is more efficient as it results in % delay of log2(N) instead of a delay of N delay % This implementation shows how to explicitly implement the vector sum in % a tree shape to enable hardware optimizations. % The ideal way to code this generically for any length of 'u' is to use % recursion but it is not currently supported by MATLAB Coder % NOTE: To instruct MATLAB Coder to compile an external function, % add the following compilation directive or pragma to the function code %#codegen % This implementation is hardwired for a 40tap filter. level1 = vsum(u); level2 = vsum(level1); level3 = vsum(level2); level4 = vsum(level3); level5 = vsum(level4); level6 = vsum(level5); y = level6; function output = vsum(input) coder.inline('always'); vt = input(1:2:end); for i = int32(1:numel(input)/2) k = int32(i*2); vt(i) = vt(i) + input(k); end output = vt; function tap_delay = mtapped_delay_fcn(input) % The Tapped Delay function delays its input by the specified number % of sample periods, and outputs all the delayed versions in a vector % form. The output includes current input % NOTE: To instruct MATLAB Coder to compile an external function, % add the following compilation directive or pragma to the function code %#codegen persistent u_d; if isempty(u_d) u_d = zeros(1,40); end u_d = [u_d(2:40), input]; tap_delay = u_d; function weights = update_weight_fcn(step_size, err_sig, ... delayed_signal, filter_coeff, reset_weights) % This function updates the adaptive filter weights based on LMS algorithm % Copyright 2007-2022 The MathWorks, Inc. % NOTE: To instruct MATLAB Coder to compile an external function, % add the following compilation directive or pragma to the function code %#codegen step_sig = step_size .* err_sig; correction_factor = delayed_signal .* step_sig; updated_weight = correction_factor + filter_coeff; if reset_weights weights = zeros(1,40); else weights = updated_weight; end
The MATLAB function is modular and uses functions:
mtapped_delay_fcnto calculate delayed versions of the input signal in vector form.mtreesum_fcnto calculate the sum of the applied weights in a tree structure. The individual sum is calculated by using avsumfunction.update_weight_fcnto calculate the updated filter weights based on the least mean square algorithm.
LMS Filter MATLAB Test Bench
Review the MATLAB test bench:
open(testbench_name)
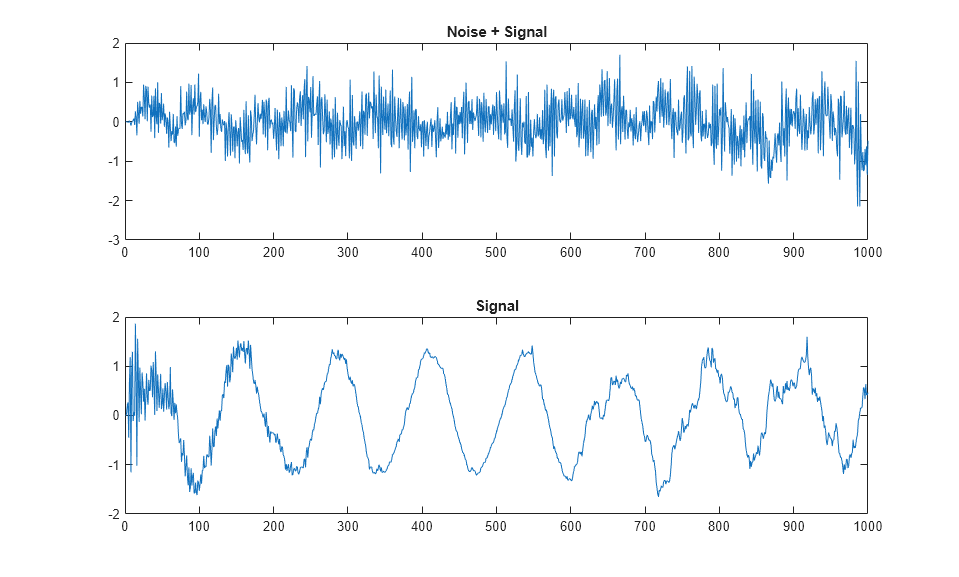
% Returns an adaptive FIR filter System object, % HLMS, that computes the filtered output, filter error and the filter % weights for a given input and desired signal using the Least Mean % Squares (LMS) algorithm. % Copyright 2011-2022 The MathWorks, Inc. clear('mlhdlc_lms_fcn'); hfilt2 = dsp.FIRFilter(... 'Numerator', fir1(10, [.5, .75])); rng('default'); % always default to known state x = randn(1000,1); % Noise d = step(hfilt2, x) + sin(0:.05:49.95)'; % Noise + Signal stepSize = 0.01; reset_weights =false; hSrc = dsp.SignalSource(x); hDesiredSrc = dsp.SignalSource(d); hOut = dsp.SignalSink; hErr = dsp.SignalSink; %%%%%%%%%%%%%%%%%%%%%%%%%%%% %Call to the design %%%%%%%%%%%%%%%%%%%%%%%%%%%% while (~isDone(hSrc)) [y, e] = mlhdlc_lms_fcn(step(hSrc), step(hDesiredSrc), ... stepSize, reset_weights); step(hOut, y); step(hErr, e); end figure('Name', [mfilename, '_signal_plot']); subplot(2,1,1), plot(hOut.Buffer), title('Noise + Signal'); subplot(2,1,2),plot(hErr.Buffer), title('Signal');
Test the MATLAB Algorithm
To avoid run-time errors, simulate the design with the test bench.
mlhdlc_lms_noise_canceler_tb
Create an HDL Coder Project
To generate HDL code from a MATLAB design:
1. Create a HDL Coder project:
coder -hdlcoder -new mlhdlc_lms_nc
2. Add the file mlhdlc_lms_fcn.m to the project as the MATLAB Function and mlhdlc_lms_noise_canceler_tb.m as the MATLAB Test Bench.
3. Click Autodefine types to use the recommended types for the inputs and outputs of the MATLAB function mlhdlc_lms_fcn.
For a more complete tutorial on creating and populating MATLAB HDL Coder projects, see Get Started with MATLAB to HDL Workflow.

Run Fixed-Point Conversion and HDL Code Generation
Click the Workflow Advisor button to start the Workflow Advisor.
Right click the HDL Code Generation task and select Run to selected task.
A single HDL file mlhdlc_lms_fcn_FixPt.vhd is generated for the MATLAB design. To examine the generated HDL code for the filter design, click the hyperlinks in the Code Generation Log window.
If you want to generate a HDL file for each function in your MATLAB design, in the Advanced tab of the HDL Code Generation task, select the Generate instantiable code for functions check box. See also Generate Instantiable Code for Functions.