usamap
Create axesm-based map for United States of America
Syntax
Description
usamap andstate
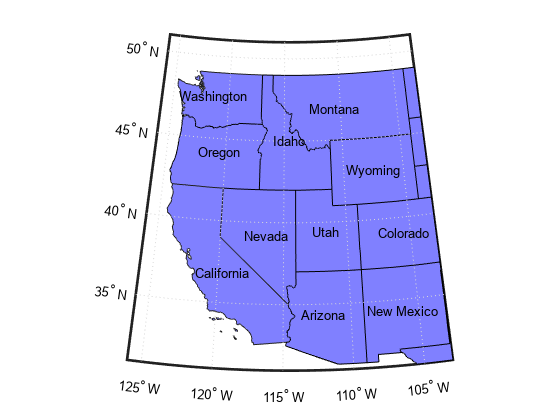
usamap( create an empty
state)axesm-based map (previously referred to as map axes)
with a Lambert Conformal Conic projection and map limits covering a U.S. state
or group of states specified by state. The
axesm-based map is created in the current axes and the
axis limits are set tight around the map frame.
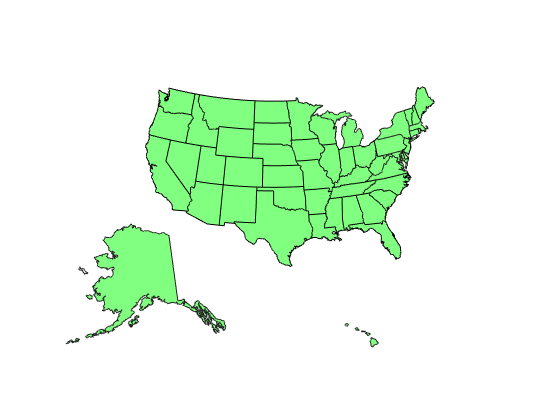
usamap 'conus' and
usamap('conus') create an empty
axesm-based map for the conterminous 48 states (that
is, all states excluding Alaska and Hawaii).
usamap with no arguments presents a menu from which you
can select a single state, the District of Columbia, the conterminous 48 states,
or all states.
h = usamap(___)axesm-based map.
h = usamap('all')axesm-based maps, inset within a single figure, for
the conterminous states, Alaska, and Hawaii, with a spherical Earth model and
other projection parameters suggested by the U.S. Geological Survey. The maps in
the three axes are shown at approximately the same scale. The handles for the
three axesm-based maps are returned in
h.
usamap('allequal') is the same as
usamap('all'), but usage of 'allequal'
will be removed in a future release.
Examples
Input Arguments
Output Arguments
Tips
All axes created with
usamapare initialized with a spherical Earth model having a radius of 6,371,000 meters.In some cases,
usamapusestightmapto adjust the axis limits tight around the map. If you change the projection, or just want more white space around the map frame, usetightmapagain oraxis auto.axes(h(n)), wheren = 1,2, or3, makes the desired axes current.set(h,'Visible','on')makes the axes visible.axesscale(h(1))resizes the axes containing Alaska and Hawaii to the same scale as the conterminous states.
Version History
Introduced before R2006a