Graphical Comparison of Exponential Functions
This example shows an interesting graphical approach for discovering whether is greater than .
The question is: which is greater, or ? The easy way to find out is to type it directly at the MATLAB® command prompt. But another way to analyze the situation is to ask a more general question: what is the shape of the function ?
Here is a plot of .
% Define the mesh x = 0:0.16:5; y = 0:0.16:5; [xx,yy] = meshgrid(x,y); % The plot zz = xx.^yy-yy.^xx; h = surf(x,y,zz); h.EdgeColor = [0.7 0.7 0.7]; view(20,50); colormap(hsv); title('$z = x^y-y^x$','Interpreter','latex') xlabel('x') ylabel('y') hold on
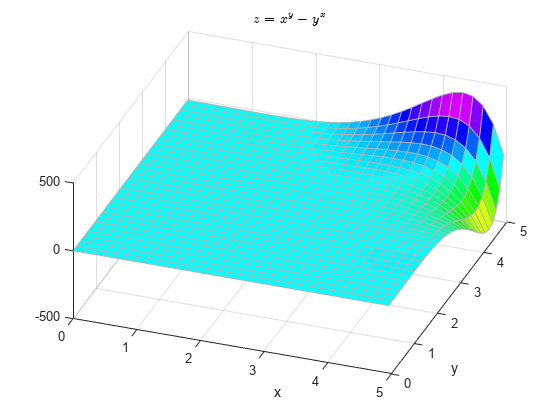
The solution of the equation has a very interesting shape, and our original question is not easily solved by inspection. Here is a plot of the xy values that yield .
c = contourc(x,y,zz,[0 0]); list1Len = c(2,1); xContour = [c(1,2:1+list1Len) NaN c(1,3+list1Len:size(c,2))]; yContour = [c(2,2:1+list1Len) NaN c(2,3+list1Len:size(c,2))]; % Note that the NAN above prevents the end of the first contour line from being % connected to the beginning of the second line line(xContour,yContour,'Color','k');
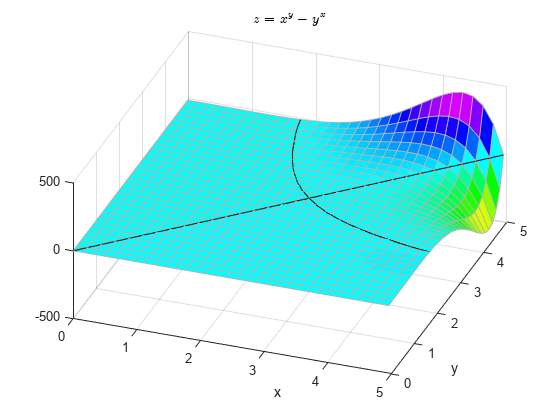
Some combinations of x and y along the black curve are integers. This next plot is of the integer solutions to the equation . Notice that is the only integer solution where .
plot([0:5 2 4],[0:5 4 2],'r.','MarkerSize',25);
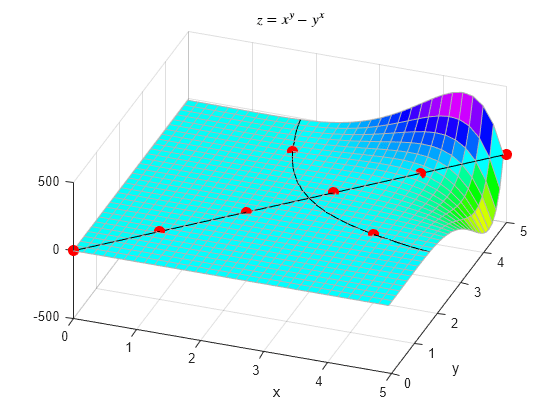
Finally, plot the points and on the surface. The result shows that is indeed larger than (though not by much).
e = exp(1); plot([e pi],[pi e],'r.','MarkerSize',25); plot([e pi],[pi e],'y.','MarkerSize',10); text(e,3.3,'(e,pi)','Color','k', ... 'HorizontalAlignment','left','VerticalAlignment','bottom'); text(3.3,e,'(pi,e)','Color','k','HorizontalAlignment','left',... 'VerticalAlignment','bottom'); hold off;
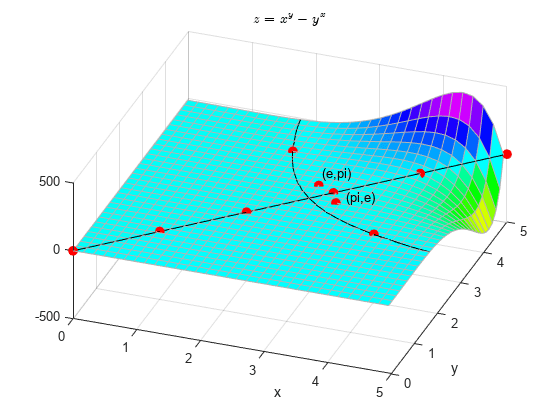
Verify the results.
e = exp(1); e^pi
ans = 23.1407
pi^e
ans = 22.4592
