bvpinit
Form initial guess for boundary value problem solver
Description
solinit = bvpinit(sol,[anew bnew])[anew bnew],
where sol is a solution structure obtained from
bvp4c or bvp5c. The new interval [anew
bnew] must be larger than the previous interval on which sol
is defined. The previous solution sol is extrapolated to the new
interval.
solinit = bvpinit(___,parameters)
Examples
Initial Guess of BVP Solution
Create an initial guess of the solution to a BVP, solve the BVP with bvp4c, and then extend the solution to a new domain.
Forming a good initial guess of the solution to a BVP problem is perhaps the most difficult part of solving the problem. BVP solutions are not necessarily unique, so the initial guess can be the deciding factor in which of many solutions the solver returns. The initial guess should satisfy the boundary conditions, and the behavior inbetween should reflect your general expectations about the problem (whether the solution oscillates, is a simple linear function, and so on...).
Consider the differential equation
.
The equation is subject to the boundary conditions
.
The function that encodes the equation as a first-order system is
function dydx = bvpfun(x,y) dydx = [y(2) -y(1)]; end
Similarly, the function that encodes the boundary conditions is
function res = bcfun(ya,yb) res = [ya(1) yb(1)]; end
You either can include the required functions as local functions at the end of a file (as done here), or you can save them as separate, named files in a directory on the MATLAB® path.
Initial Guess with Function Handle
You reasonably can expect the solution to the equation to be oscillatory, so sine and cosine functions are a good initial guess of the behavior of the solution and its derivative between the fixed boundary points.
function y = guess(x) y = [sin(x) cos(x)]; end
Create a solution structure using 10 equally spaced mesh points in the domain and the initial guess function.
xmesh = linspace(0,pi,10); solinit = bvpinit(xmesh,@guess);
Solve BVP
Call bvp4c with the ode function, boundary conditions, and solution guess. Plot the result.
sol = bvp4c(@bvpfun, @bcfun, solinit);
plot(sol.x,sol.y,'-o')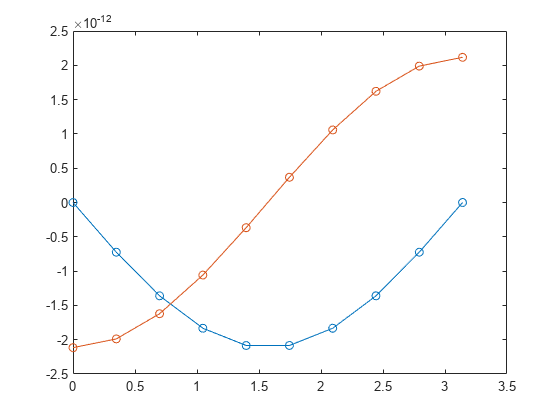
Local Functions
Listed here are the local helper functions that the BVP solver bvp4c calls to calculate the solution. Alternatively, you can save these functions as their own files in a directory on the MATLAB path.
function dydx = bvpfun(x,y) % equation being solved dydx = [y(2) -y(1)]; end %------------------------------------------- function res = bcfun(ya,yb) % boundary conditions res = [ya(1) yb(1)]; end %------------------------------------------- function y = guess(x) % guess at solution behavior y = [sin(x) cos(x)]; end %-------------------------------------------
Extend BVP Solution with Extrapolation
Solve a BVP over an initial interval, and then iteratively extend the interval using each solution as the initial guess for the next interval.
Consider the equation
.
As a first-order system, the equation becomes a system of two equations
,
.
The equation is initially defined on the interval and is subject to the boundary conditions
,
.
The function that encodes the equation as a first-order system is
function dydx = bvpfun(x,y) dydx = [y(2) y(1)]; end
Similarly, the function that encodes the boundary conditions is
function res = bcfun(ya,yb) res = [ya(1) yb(1)-1]; end
You either can include the required functions as local functions at the end of a file (as done here), or you can save them as separate, named files in a directory on the MATLAB path.
Initial Guess
Use an exponential function as the initial guess for the solution. Since the equation has two solution components, write an initial guess function of the form y = guess(x) that returns a vector.
function y = guess(x) y = [exp(x) exp(x)]; end
A mesh of five points is sufficient to capture the behavior of the guess function.
xmesh = linspace(0,3,5); solinit = bvpinit(xmesh,@guess);
Solve Equation
Solve the equation in the initial interval and plot the results for .
sol = bvp4c(@bvpfun, @bcfun, solinit);
plot(sol.x(1,:),sol.y(1,:),'-o')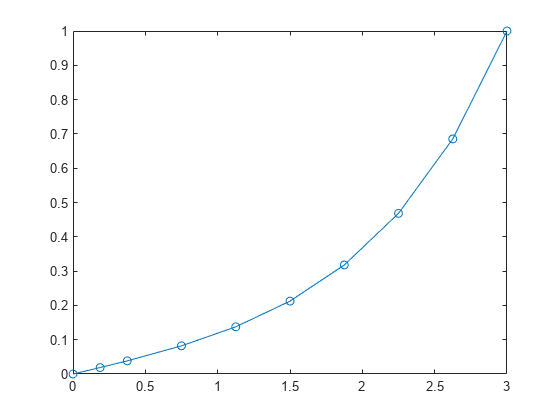
Extend Interval
Now, use bvpinit to extend the interval of integration in a loop, solving and plotting each new problem. In each iteration, form the initial guess using the previous solution sol extrapolated to the new interval [0 k]. In each new problem, bvp4c enforces the boundary conditions at the new boundaries [0 k].
hold on for k = 4:8 solinit = bvpinit(sol,[0 k]); sol = bvp4c(@bvpfun, @bcfun, solinit); plot(sol.x(1,:),sol.y(1,:),'-o') end
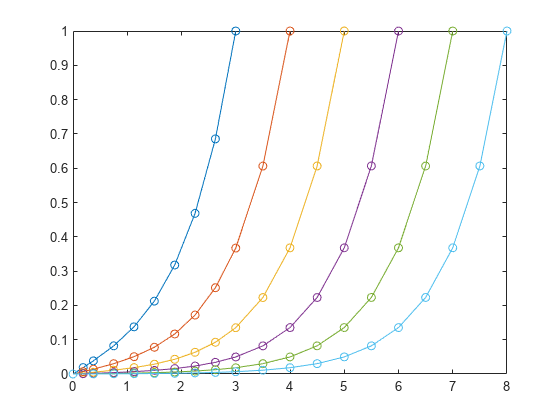
This example shows a simplified version of continuation, a useful technique to solve BVPs by breaking the problem down into smaller intervals or simpler problems. For more examples of this technique, see:
Local Functions
Listed here are the local helper functions that the BVP solver bvp4c calls to calculate the solution. Alternatively, you can save these functions as their own files in a directory on the MATLAB path.
function dydx = bvpfun(x,y) % equation being solved dydx = [y(2) y(1)]; end %------------------------------------------- function res = bcfun(ya,yb) % boundary conditions res = [ya(1) yb(1)-1]; end %------------------------------------------- function y = guess(x) % guess at solution behavior y = [exp(x) exp(x)]; end %-------------------------------------------
Input Arguments
x — Initial mesh
vector
Initial mesh, specified as a vector. To solve the problem on the interval
[a,b], specify x(1) as
a and x(end) as b. The
entries of x must be in increasing order (if a < b) or decreasing order (if a > b). The solver adapts this mesh to the solution (by adding, removing,
and moving the mesh points), so a guess like x = linspace(a,b,10)
often suffices. To handle difficult problems, place some mesh points where the solution
changes rapidly.
For two-point boundary value problems, the entries of
xmust be unique. That is, if a < b, the entries must satisfyx(1)<x(2)< ... <x(end). If a > b, the entries must satisfyx(1)>x(2)> ... >x(end).For multipoint boundary value problems, you can specify the points in [a,b] at which the boundary conditions apply, other than the endpoints a and b, by repeating their entries in
x. For example, consider the vectorFor this mesh, the boundary conditions apply at three points: the endpointsx = [0 0.5 1 1 1.5 2];
0and2, and the repeated entry1. In general, repeated entries represent boundary points between regions in [a,b]. The repeated entry1divides the interval[0 2]into two regions:[0 1]and[1 2].
Example: solinit = bvpinit(linspace(a,b,10),yinit)
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Complex Number Support: Yes
yinit — Initial guess of solution
vector | function
Initial guess of solution, specified as a vector or a function.
Vector – For each component of the solution,
bvpinitreplicates the corresponding element of the vector as a constant guess across all mesh points. That is,yinit(i)is a constant guess for theith componentyinit(i,:)of the solution at all the mesh points inx.Function – For a given mesh point, the guess function must return a vector whose elements are guesses for the corresponding components of the solution. The function must be of the form
y = guess(x)
xis a mesh point andyis a vector whose length is the same as the number of components in the solution. For example, ifyinitis a function, then at each mesh pointbvpinitcallsy(:,j) = guess(x(j))
For multipoint boundary value problems, the guess function must be of the form
y = guess(x,k)
yis an initial guess for the solution atxin regionk. The function must accept the input argumentk, which is provided for flexibility in writing the guess function. However, the function is not required to usek.
Example: solinit = bvpinit(x,[sqrt(3)/2; 0])
Example: solinit = bvpinit(x,@guess)
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char | function_handle
Complex Number Support: Yes
parameters — Initial guess for unknown parameter values
scalar | vector
Initial guess for unknown parameter values, specified as a scalar or vector.
Example: solinit = bvpinit(x, yinit, [0 1 sqrt(2)]) specifies a
vector of guesses for three unknown parameters.
Example: Type edit mat4bvp to see an example of a BVP with an
unknown parameter.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Complex Number Support: Yes
sol — Prior solution
structure
Prior solution, specified as a solution structure returned by
bvp4c or bvp5c. If sol
contains parameters, they are copied to solinit.
Data Types: struct
Output Arguments
Extended Capabilities
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)