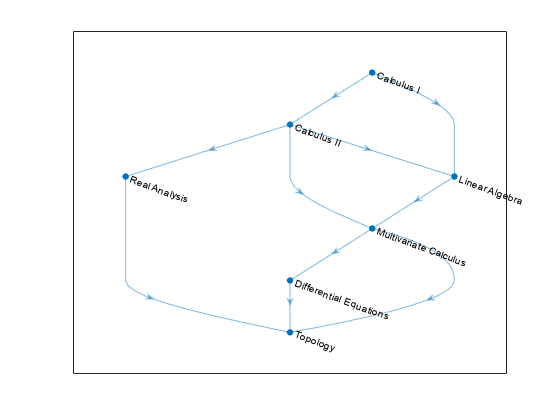
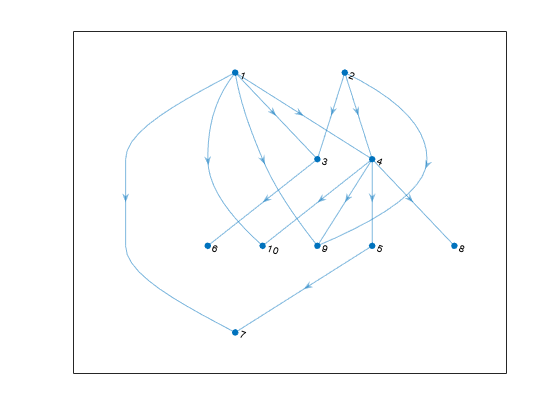
toposort
Topological order of directed acyclic graph
Description
n = toposort(G)G such that i < j for every edge
(n(i),n(j)) in G. The directed graph
G cannot have any cycles.
Examples
Input Arguments
Output Arguments
More About
Version History
Introduced in R2015b
See Also
digraph | isdag | reordernodes