eigs
Subset of eigenvalues and eigenvectors
Syntax
Description
d = eigs(A,k,sigma,Name,Value)eigs(A,k,sigma,'Tolerance',1e-3) adjusts the
convergence tolerance for the algorithm.
Examples
Largest Eigenvalues of Sparse Matrix
The matrix A = delsq(numgrid('C',15)) is a symmetric positive definite matrix with eigenvalues reasonably well-distributed in the interval (0 8). Compute the six largest magnitude eigenvalues.
A = delsq(numgrid('C',15));
d = eigs(A)d = 6×1
7.8666
7.7324
7.6531
7.5213
7.4480
7.3517
Specify a second input to compute a specific number of the largest eigenvalues.
d = eigs(A,3)
d = 3×1
7.8666
7.7324
7.6531
Smallest Eigenvalues of Sparse Matrix
The matrix A = delsq(numgrid('C',15)) is a symmetric positive definite matrix with eigenvalues reasonably well-distributed in the interval (0 8). Compute the five smallest eigenvalues.
A = delsq(numgrid('C',15)); d = eigs(A,5,'smallestabs')
d = 5×1
0.1334
0.2676
0.3469
0.4787
0.5520
Eigenvalues Using Function Handle
Create a 1500-by-1500 random sparse matrix with a 25% approximate density of nonzero elements.
n = 1500; A = sprand(n,n,0.25);
Find the LU factorization of the matrix, returning a permutation vector p that satisfies A(p,:) = L*U.
[L,U,p] = lu(A,'vector');Create a function handle Afun that accepts a vector input x and uses the results of the LU decomposition to, in effect, return A\x.
Afun = @(x) U\(L\(x(p)));
Calculate the six smallest magnitude eigenvalues using eigs with the function handle Afun. The second input is the size of A.
d = eigs(Afun,1500,6,'smallestabs')d = 6×1 complex
0.1423 + 0.0000i
0.4859 + 0.0000i
-0.3323 - 0.3881i
-0.3323 + 0.3881i
0.1019 - 0.5381i
0.1019 + 0.5381i
Types of Eigenvalues
west0479 is a real-valued 479-by-479 sparse matrix with both real and complex pairs of conjugate eigenvalues.
Load the west0479 matrix, then compute and plot all of the eigenvalues using eig. Since the eigenvalues are complex, plot automatically uses the real parts as the x-coordinates and the imaginary parts as the y-coordinates.
load west0479 A = west0479; d = eig(full(A)); plot(d,'+')
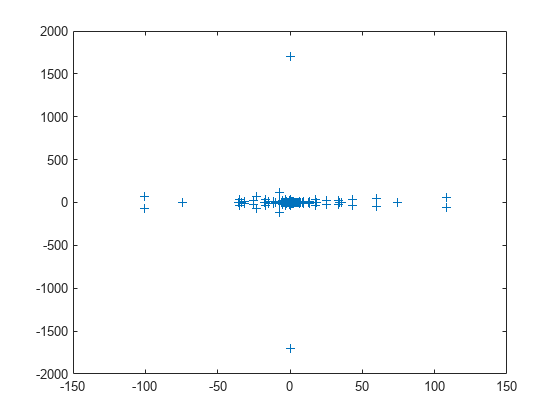
The eigenvalues are clustered along the real line (x-axis), particularly near the origin.
eigs has several options for sigma that can pick out the largest or smallest eigenvalues of varying types. Compute and plot some eigenvalues for each of the available options for sigma.
figure plot(d, '+') hold on la = eigs(A,6,'largestabs'); plot(la,'ro') sa = eigs(A,6,'smallestabs'); plot(sa,'go') hold off legend('All eigenvalues','Largest magnitude','Smallest magnitude') xlabel('Real axis') ylabel('Imaginary axis')
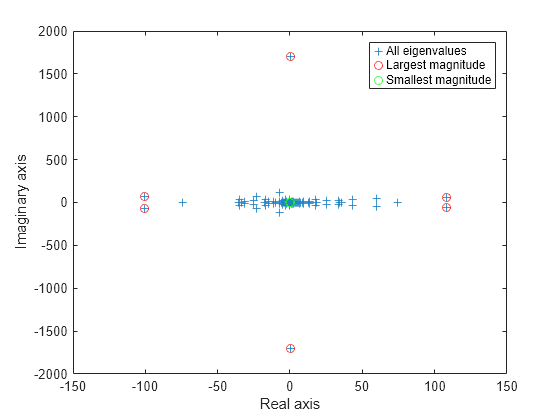
figure plot(d, '+') hold on ber = eigs(A,4,'bothendsreal'); plot(ber,'r^') bei = eigs(A,4,'bothendsimag'); plot(bei,'g^') hold off legend('All eigenvalues','Both ends real','Both ends imaginary') xlabel('Real axis') ylabel('Imaginary axis')
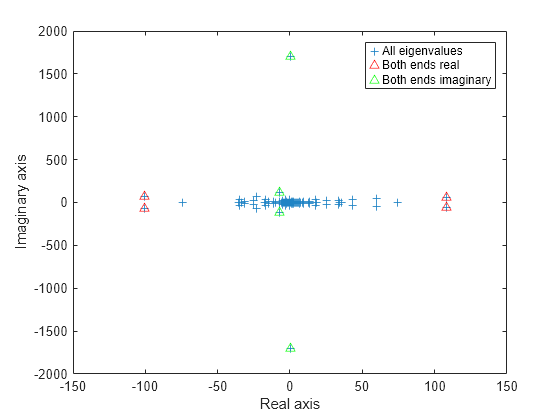
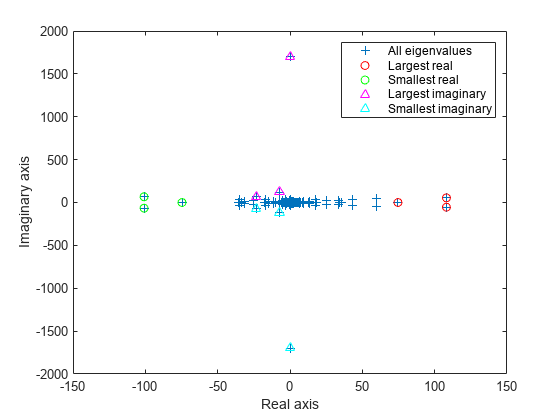
figure plot(d, '+') hold on lr = eigs(A,3,'largestreal'); plot(lr,'ro') sr = eigs(A,3,'smallestreal'); plot(sr,'go') li = eigs(A,3,'largestimag','SubspaceDimension',45); plot(li,'m^') si = eigs(A,3,'smallestimag','SubspaceDimension',45); plot(si,'c^') hold off legend('All eigenvalues','Largest real','Smallest real','Largest imaginary','Smallest imaginary') xlabel('Real axis') ylabel('Imaginary axis')
Difference Between 'smallestabs' and 'smallestreal' Eigenvalues
Create a symmetric positive definite sparse matrix.
A = delsq(numgrid('C', 150));Compute the six smallest real eigenvalues using 'smallestreal', which employs a Krylov method using A.
tic
d = eigs(A, 6, 'smallestreal')d = 6×1
0.0013
0.0025
0.0033
0.0045
0.0052
0.0063
toc
Elapsed time is 1.777706 seconds.
Compute the same eigenvalues using 'smallestabs', which employs a Krylov method using the inverse of A.
tic
dsm = eigs(A, 6, 'smallestabs')dsm = 6×1
0.0013
0.0025
0.0033
0.0045
0.0052
0.0063
toc
Elapsed time is 0.257572 seconds.
The eigenvalues are clustered near zero. The 'smallestreal' computation struggles to converge using A since the gap between the eigenvalues is so small. Conversely, the 'smallestabs' option uses the inverse of A, and therefore the inverse of the eigenvalues of A, which have a much larger gap and are therefore easier to compute. This improved performance comes at the cost of factorizing A, which is not necessary with 'smallestreal'.
Sigma Value Near Eigenvalue
Compute eigenvalues near a numeric sigma value that is nearly equal to an eigenvalue.
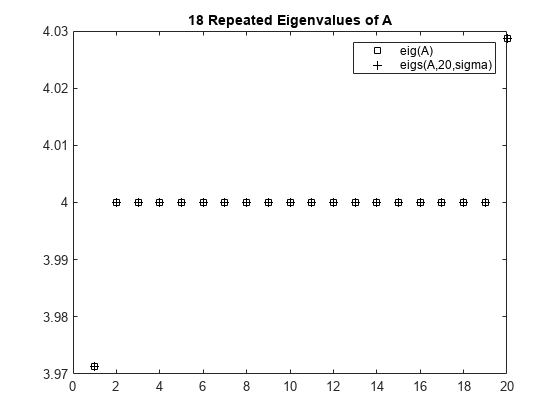
The matrix A = delsq(numgrid('C',30)) is a symmetric positive definite matrix of size 632 with eigenvalues reasonably well-distributed in the interval (0 8), but with 18 eigenvalues repeated at 4.0. To calculate some eigenvalues near 4.0, it is reasonable to try the function call eigs(A,20,4.0). However, this call computes the largest eigenvalues of the inverse of A - 4.0*I, where I is an identity matrix. Because 4.0 is an eigenvalue of A, this matrix is singular and therefore does not have an inverse. eigs fails and produces an error message. The numeric value of sigma cannot be exactly equal to an eigenvalue. Instead, you must use a value of sigma that is near but not equal to 4.0 to find those eigenvalues.
Compute all of the eigenvalues using eig, and the 20 eigenvalues closest to 4 - 1e-6 using eigs to compare results. Plot the eigenvalues calculated with each method.
A = delsq(numgrid('C',30));
sigma = 4 - 1e-6;
d = eig(A);
D = sort(eigs(A,20,sigma));plot(d(307:326),'ks') hold on plot(D,'k+') hold off legend('eig(A)','eigs(A,20,sigma)') title('18 Repeated Eigenvalues of A')
Eigenvalues of Permuted Cholesky Factor
Create sparse random matrices A and B that both have low densities of nonzero elements.
B = sprandn(1e3,1e3,0.001) + speye(1e3); B = B'*B; A = sprandn(1e3,1e3,0.005); A = A+A';
Find the Cholesky decomposition of matrix B, using three outputs to return the permutation vector s and test value p.
[R,p,s] = chol(B,'vector');
pp = 0
Since p is zero, B is a symmetric positive definite matrix that satisfies B(s,s) = R'*R.
Calculate the six largest magnitude eigenvalues and eigenvectors of the generalized eigenvalue problem involving A and R. Since R is the Cholesky factor of B, specify 'IsCholesky' as true. Furthermore, since B(s,s) = R'*R and thus R = chol(B(s,s)), use the permutation vector s as the value of 'CholeskyPermutation'.
[V,D,flag] = eigs(A,R,6,'largestabs','IsCholesky',true,'CholeskyPermutation',s); flag
flag = 0
Since flag is zero, all of the eigenvalues converged.
Input Arguments
A — Input matrix
matrix
Input matrix, specified as a square matrix. A is
typically, but not always, a large and sparse matrix.
If A is symmetric, then eigs uses a specialized
algorithm for that case. If A is
nearly symmetric, then consider using A =
(A+A')/2 to make A symmetric before calling
eigs. This ensures that eigs
calculates real eigenvalues instead of complex ones.
Data Types: double
Complex Number Support: Yes
B — Input matrix
matrix
Input matrix, specified as a square matrix of the same size as A. When
B is specified, eigs solves the
generalized eigenvalue problem A*V = B*V*D.
If B is symmetric positive definite, then eigs uses a
specialized algorithm for that case. If B is
nearly symmetric positive definite, then consider
using B = (B+B')/2 to make B symmetric
before calling eigs.
When A is scalar, you can specify B
as an empty matrix eigs(A,[],k) to solve the standard
eigenvalue problem and disambiguate between B and
k.
Data Types: double
Complex Number Support: Yes
k — Number of eigenvalues to compute
scalar
Number of eigenvalues to compute, specified as a positive scalar integer. If
k is larger than size(A,2), then
eigs uses the maximum valid value k =
size(A,2) instead.
Example: eigs(A,2) returns the two largest
eigenvalues of A.
sigma — Type of eigenvalues
'largestabs' (default) | 'smallestabs' | 'largestreal' | 'smallestreal' | 'bothendsreal' | 'largestimag' | 'smallestimag' | 'bothendsimag' | scalar
Type of eigenvalues, specified as one of the values in the table.
|
sigma |
Description | sigma (R2017a and earlier) |
|---|---|---|
|
scalar (real or complex, including 0) |
The eigenvalues closest to the number
| No change |
|
|
Largest magnitude. | 'lm'
|
|
|
Smallest magnitude. Same as | 'sm'
|
|
|
Largest real. | 'lr', 'la' |
|
|
Smallest real. | 'sr', 'sa' |
|
|
Both ends, with | 'be' |
For nonsymmetric problems,
sigma also can be:
|
sigma |
Description | sigma (R2017a and earlier) |
|---|---|---|
|
|
Largest imaginary part. | 'li' if A is
complex. |
|
|
Smallest imaginary part. | 'si' if A is
complex. |
|
|
Both ends, with | 'li' if A is
real. |
Example: eigs(A,k,1) returns the k eigenvalues
closest to 1.
Example: eigs(A,k,'smallestabs') returns the k smallest
magnitude eigenvalues.
Data Types: double | char | string
opts — Options structure
structure
Options structure, specified as a structure containing one or more of the fields in this table.
Note
Use of the options structure to specify options is not recommended. Use name-value pairs instead.
| Option Field | Description | Name-Value Pair |
|---|---|---|
issym | Symmetry of | 'IsFunctionSymmetric' |
tol | Convergence tolerance. | 'Tolerance' |
maxit | Maximum number of iterations. | 'MaxIterations' |
p | Number of Lanczos basis vectors. | 'SubspaceDimension' |
v0 | Starting vector. | 'StartVector' |
disp | Diagnostic information display level. | 'Display' |
fail | Treatment of nonconverged eigenvalues in the output. | 'FailureTreatment' |
spdB | Is B symmetric positive
definite? | 'IsSymmetricDefinite' |
cholB | Is | 'IsCholesky' |
permB | Specify the permutation vector | 'CholeskyPermutation' |
Example: opts.issym = 1, opts.tol = 1e-10 creates
a structure with values set for the fields issym and tol.
Data Types: struct
Afun — Matrix function
function handle
Matrix function, specified as a function handle. The function y = Afun(x)
must return the proper value depending on the sigma input:
A*x— Ifsigmais unspecified or any text option other than'smallestabs'.A\x— Ifsigmais0or'smallestabs'.(A-sigma*I)\x— Ifsigmais a nonzero scalar (for standard eigenvalue problem).(A-sigma*B)\x— Ifsigmais a nonzero scalar (for generalized eigenvalue problem).
For example, the following Afun works when calling eigs
with sigma = 'smallestabs':
[L,U,p] = lu(A,'vector'); Afun = @(x) U\(L\(x(p))); d = eigs(Afun,100,6,'smallestabs')
For a generalized eigenvalue problem, add matrix B as
follows (B cannot be represented by a function
handle):
d = eigs(Afun,100,B,6,'smallestabs')
A is assumed to be nonsymmetric unless
'IsFunctionSymmetric' (or
opts.issym) specifies otherwise. Setting
'IsFunctionSymmetric' to true
ensures that eigs calculates real eigenvalues instead
of complex ones.
For information on how to provide additional parameters to the
Afun function, see Parameterizing Functions.
Tip
Call eigs with the 'Display'
option turned on to see what output is expected from
Afun.
n — Size of square matrix represented by Afun
scalar
Size of square matrix A that is represented by
Afun, specified as a positive scalar integer.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: d =
eigs(A,k,sigma,'Tolerance',1e-10,'MaxIterations',100) loosens the
convergence tolerance and uses fewer iterations.
Tolerance — Convergence tolerance
1e-14 (default) | positive real scalar
Convergence tolerance, specified as the comma-separated pair
consisting of 'Tolerance' and a positive real numeric
scalar.
Example: s =
eigs(A,k,sigma,'Tolerance',1e-3)
MaxIterations — Maximum number of algorithm iterations
300 (default) | positive integer
Maximum number of algorithm iterations, specified as the
comma-separated pair consisting of 'MaxIterations'
and a positive integer.
Example: d =
eigs(A,k,sigma,'MaxIterations',350)
SubspaceDimension — Maximum size of Krylov subspace
max(2*k,20) (default) | nonnegative integer
Maximum size of Krylov subspace, specified as the comma-separated pair
consisting of 'SubspaceDimension' and a nonnegative
integer. The 'SubspaceDimension' value must be
greater than or equal to k + 1 for real symmetric
problems, and k + 2 otherwise, where
k is the number of eigenvalues.
The recommended value is p >= 2*k, or for real
nonsymmetric problems, p >= 2*k+1. If you do not
specify a 'SubspaceDimension' value, then the default
algorithm uses at least 20 Lanczos vectors.
For problems where eigs fails to converge,
increasing the value of 'SubspaceDimension' can
improve the convergence behavior. However, increasing the value too much
can cause memory issues.
Example: d =
eigs(A,k,sigma,'SubspaceDimension',25)
StartVector — Initial starting vector
random vector (default) | vector
Initial starting vector, specified as the comma-separated pair
consisting of 'StartVector' and a numeric
vector.
The primary reason to specify a different random starting vector is when you want to control the random number stream used to generate the vector.
Note
eigs selects the starting vectors in a
reproducible manner using a private random number stream. Changing
the random number seed does not affect the
starting vector.
Example: d =
eigs(A,k,sigma,'StartVector',randn(m,1)) uses a random
starting vector that draws values from the global random number
stream.
Data Types: double
FailureTreatment — Treatment of nonconverged eigenvalues
'replacenan' (default) | 'keep' | 'drop'
Treatment of nonconverged eigenvalues, specified as the
comma-separated pair consisting of 'FailureTreatment'
and one of the options: 'replacenan',
'keep', or 'drop'.
The value of 'FailureTreatment' determines how
eigs displays nonconverged eigenvalues in the
output.
|
Option |
Affect on output |
|---|---|
|
|
Replace nonconverged eigenvalues with
|
|
|
Include nonconverged eigenvalues in the output. |
|
|
Remove nonconverged eigenvalues from the output.
This option can result in |
Example: d =
eigs(A,k,sigma,'FailureTreatment','drop') removes
nonconverged eigenvalues from the output.
Data Types: char | string
Display — Toggle for diagnostic information display
false or
0 (default) | true or 1
Toggle for diagnostic information display, specified as the
comma-separated pair consisting of 'Display' and a
numeric or logical 1 (true) or
0 (false). Specify a value of
true or 1 to turn on the
display of diagnostic information during the calculation.
AfunIsFunctionSymmetric — Symmetry of Afun matrix
true or 1 | false or 0
Symmetry of Afun matrix, specified as the
comma-separated pair consisting of
'IsFunctionSymmetric' and a numeric or logical
1 (true) or
0 (false).
This option specifies whether the matrix that Afun
applies to its input vector is symmetric. Specify a value of
true or 1 to indicate that
eigs should use a specialized algorithm for the
symmetric matrix and return real eigenvalues.
A*V =
B*V*DIsCholesky — Cholesky decomposition toggle for B
true or 1 | false or 0
Cholesky decomposition toggle for B, specified as
the comma-separated pair consisting of 'IsCholesky'
and a numeric or logical 1 (true)
or 0 (false).
This option specifies whether the input for matrix
B in the call eigs(A,B,___) is
actually the Cholesky factor R produced by R
= chol(B).
Note
Do not use this option if sigma is
'smallestabs' or a numeric scalar.
CholeskyPermutation — Cholesky permutation vector
1:n (default) | vector
Cholesky permutation vector, specified as the comma-separated pair
consisting of 'CholeskyPermutation' and a numeric
vector. Specify the permutation vector permB if
sparse matrix B is reordered before factorization
according to chol(B(permB,permB)).
You also can use the three-output syntax of chol
for sparse matrices to directly obtain permB with
[R,p,permB] = chol(B,'vector').
Note
Do not use this option if sigma is
'smallestabs' or a numeric scalar.
IsSymmetricDefinite — Symmetric-positive-definiteness toggle for B
true or 1 | false or 0
Symmetric-positive-definiteness toggle for B,
specified as the comma-separated pair consisting of
'IsSymmetricDefinite' and a numeric or logical
1 (true) or
0 (false). Specify
true or 1 when you know that
B is symmetric positive definite, that is, it is
a symmetric matrix with strictly positive eigenvalues.
If B is symmetric positive semi-definite (some
eigenvalues are zero), then specifying
'IsSymmetricDefinite' as true
or 1 forces eigs to use the same
specialized algorithm that it uses when B is
symmetric positive definite.
Note
To use this option, the value of sigma must be
numeric or 'smallestabs'.
Output Arguments
d — Eigenvalues
column vector
Eigenvalues, returned as a column vector. d is sorted differently depending
on the value of sigma.
|
Value of |
Output sorting |
|---|---|
|
|
Descending order by magnitude |
|
|
Descending order by real part |
|
|
Descending order by imaginary part |
|
|
Ascending order by magnitude |
|
|
Ascending order by real part |
|
|
Ascending order by imaginary part |
|
|
Descending order by absolute value of imaginary part |
V — Eigenvectors
matrix
Eigenvectors, returned as a matrix. The columns in V correspond to the
eigenvalues along the diagonal of D. The form and
normalization of V depends on the combination of input
arguments:
[V,D] = eigs(A)returns matrixV, whose columns are the right eigenvectors ofAsuch thatA*V = V*D. The eigenvectors inVare normalized so that the 2-norm of each is 1.If
Ais symmetric, then the eigenvectors,V, are orthonormal.[V,D] = eigs(A,B)returnsVas a matrix whose columns are the generalized right eigenvectors that satisfyA*V = B*V*D. The 2-norm of each eigenvector is not necessarily 1.If
Bis symmetric positive definite, then the eigenvectors inVare normalized so that theB-norm of each is 1. IfAis also symmetric, then the eigenvectors areB-orthonormal.
Different machines, releases of MATLAB®, or parameters (such as the starting vector and subspace dimension) can produce different eigenvectors that are still numerically accurate:
For real eigenvectors, the sign of the eigenvectors can change.
For complex eigenvectors, the eigenvectors can be multiplied by any complex number of magnitude 1.
For a multiple eigenvalue, its eigenvectors can be recombined through linear combinations. For example, if Ax = λx and Ay = λy, then A(x+y) = λ(x+y), so x+y also is an eigenvector of A.
D — Eigenvalue matrix
matrix
Eigenvalue matrix, returned as a diagonal matrix with the eigenvalues on the main diagonal.
flag — Convergence flag
0 | 1
Convergence flag, returned as 0 or 1. A value of
0 indicates that all the eigenvalues converged.
Otherwise, not all of the eigenvalues converged.
Use of this convergence flag output suppresses warnings about failed convergence.
Tips
eigsgenerates the default starting vector using a private random number stream to ensure reproducibility across runs. Setting the random number generator state usingrngbefore callingeigsdoes not affect the output.Using
eigsis not the most efficient way to find a few eigenvalues of small, dense matrices. For such problems, it might be quicker to useeig(full(A)). For example, finding three eigenvalues in a 500-by-500 matrix is a relatively small problem that is easily handled witheig.If
eigsfails to converge for a given matrix, increase the number of Lanczos basis vectors by increasing the value of'SubspaceDimension'. As secondary options, adjusting the maximum number of iterations,'MaxIterations', and the convergence tolerance,'Tolerance', also can help with convergence behavior.
References
[1] Stewart, G.W. "A Krylov-Schur Algorithm for Large Eigenproblems." SIAM Journal of Matrix Analysis and Applications. Vol. 23, Issue 3, 2001, pp. 601–614.
[2] Lehoucq, R.B., D.C. Sorenson, and C. Yang. ARPACK Users' Guide. Philadelphia, PA: SIAM, 1998.
Extended Capabilities
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006aR2017b: Behavior and algorithm change
Changes to sorting order of output
eigsnow sorts the output according to the value ofsigma. For example, the commandeigs(A,k,'largestabs')produceskeigenvalues sorted in descending order by magnitude.Previously, the sorting order of the output produced by
eigswas not guaranteed.Reproducibility
Calling
eigsmultiple times in succession now produces the same result. Set'StartVector'to a random vector to change this behavior.Display
A display value of
2no longer returns timing information. Instead,eigstreats a value of2the same as a value of1. Also, the messages shown by the'Display'option have changed. The new messages show the residual in each iteration, instead of the Ritz values.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)