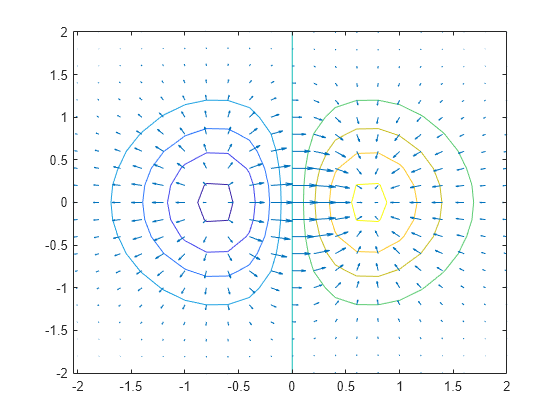
gradient
Numerical gradient
Syntax
Description
FX = gradient(F)F. The output FX corresponds
to ∂F/∂x, which
are the differences in the x (horizontal) direction.
The spacing between points is assumed to be 1.
[ returns the x and y components
of the two-dimensional numerical
gradient of matrix FX,FY]
= gradient(F)F. The additional output FY corresponds
to ∂F/∂y, which
are the differences in the y (vertical) direction.
The spacing between points in each direction is assumed to be 1.
Examples
Input Arguments
Output Arguments
More About
Tips
Use
diffor a custom algorithm to compute multiple numerical derivatives, rather than callinggradientmultiple times.
Algorithms
gradient calculates the central
difference for interior data points. For example, consider
a matrix with unit-spaced data, A, that has horizontal
gradient G = gradient(A). The interior gradient
values, G(:,j), are
G(:,j) = 0.5*(A(:,j+1) - A(:,j-1));
The subscript j varies between 2 and N-1,
with N = size(A,2).
gradient calculates values along the edges
of the matrix with single-sided differences:
G(:,1) = A(:,2) - A(:,1); G(:,N) = A(:,N) - A(:,N-1);
If you specify the point spacing, then gradient scales
the differences appropriately. If you specify two or more outputs,
then the function also calculates differences along other dimensions
in a similar manner. Unlike the diff function, gradient returns
an array with the same number of elements as the input.
Extended Capabilities
Version History
Introduced before R2006a