conncomp
Connected graph components
Description
bins = conncomp(G)G as bins. The bin numbers indicate which component each
node in the graph belongs to.
If
Gis an undirected graph, then two nodes belong to the same component if there is a path connecting them.If
Gis a directed graph, then two nodes belong to the same strong component only if there is a path connecting them in both directions.
bins = conncomp(G,Name,Value)conncomp(G,'OutputForm','cell') returns a cell array to
describe the connected components.
Examples
Find Graph Components
Create and plot an undirected graph with three connected components. Use conncomp to determine which component each node belongs to.
G = graph([1 1 4],[2 3 5],[1 1 1],6); plot(G)

bins = conncomp(G)
bins = 1×6
1 1 1 2 2 3
Strong and Weak Graph Components
Create and plot a directed graph, and then compute the strongly connected components and weakly connected components. Weakly connected components ignore the direction of connecting edges.
s = [1 2 2 3 3 3 4 5 5 5 8 8]; t = [2 3 4 1 4 5 5 3 6 7 9 10]; G = digraph(s,t); plot(G,'Layout','layered')
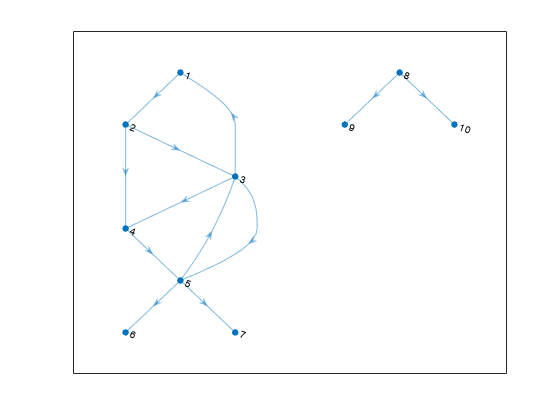
str_bins = conncomp(G)
str_bins = 1×10
4 4 4 4 4 6 5 1 3 2
weak_bins = conncomp(G,'Type','weak')
weak_bins = 1×10
1 1 1 1 1 1 1 2 2 2
Discard Graph Components Based on Size
Use the second output of conncomp to extract the largest component of a graph or to remove components below a certain size.
Create and plot a directed graph. The graph has one large component, one small component, and several components that contain only a single node.
s = [1 2 2 3 3 3 4 5 5 5 8 8 9]; t = [2 3 4 1 4 5 5 3 6 7 9 10 10]; G = digraph(s,t,[],20); plot(G,'Layout','layered')
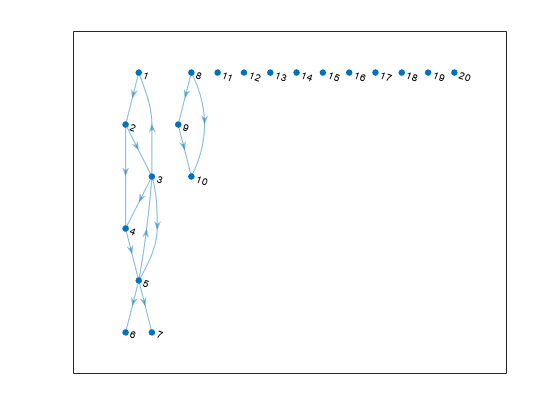
Calculate the weakly connected components and specify two outputs to conncomp to get the size of each component.
[bin,binsize] = conncomp(G,'Type','weak')
bin = 1×20
1 1 1 1 1 1 1 2 2 2 3 4 5 6 7 8 9 10 11 12
binsize = 1×12
7 3 1 1 1 1 1 1 1 1 1 1
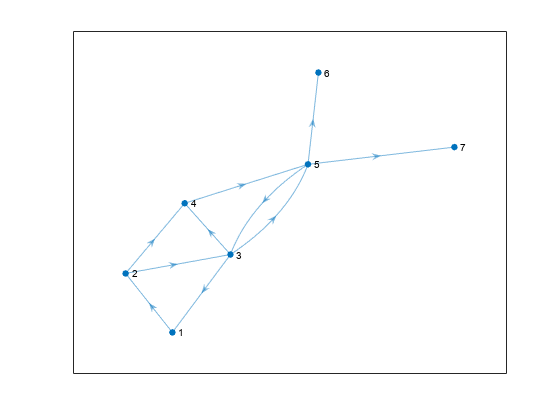
Use binsize to extract the largest component from the graph. idx is a logical index indicating whether each node belongs to the largest component. The subgraph function extracts the nodes selected by idx from G.
idx = binsize(bin) == max(binsize); SG = subgraph(G, idx); plot(SG)
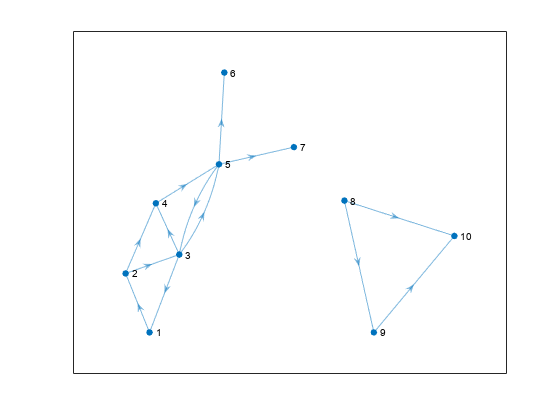
A similar use of binsizes is to filter out components based on size. The procedure is similar to extracting the largest component, however in this case each node can belong to any component that meets the size requirement.
Filter out any components in G that have fewer than 3 nodes. idx is a logical index indicating whether each node belongs to a component with 3 or more nodes.
idx = binsize(bin) >= 3; SG = subgraph(G, idx); plot(SG)
Input Arguments
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: bins = conncomp(G,'OutputForm','cell')
OutputForm — Type of output
'vector' (default) | 'cell'
Type of output, specified as the comma-separated pair consisting of
'OutputForm' and either
'vector' or 'cell'.
| Option | Output |
|---|---|
'vector' (default) | bins is a numeric vector
indicating which connected component each node belongs
to. |
'cell' | bins is a cell array, and
bins{j} contains the node IDs for
all nodes that belong to component
j. |
Type — Type of connected components
'strong' (default) | 'weak'
Note
The 'Type' option is supported only for
directed graphs created using digraph.
Type of connected components, specified as the comma-separated pair
consisting of 'Type' and either
'strong' (default) or
'weak'.
| Option | Result |
|---|---|
'strong' (default) | Two nodes belong to the same connected component only if there is a path connecting them in both directions. |
'weak' | Two nodes belong to the same connected component if there is a path connecting them, ignoring edge directions. |
Example: bins = conncomp(G,'Type','weak') computes
the weakly connected components of directed graph
G.
Output Arguments
bins — Connected components
vector | cell array
Connected components, returned as a vector or cell array. The bin numbers assign each node in the graph to a connected component:
If
OutputFormis'vector'(default), thenbinsis a numeric vector indicating which connected component (bin) each node belongs to.If
OutputFormis'cell', thenbinsis a cell array, withbins{j}containing the node IDs for all nodes that belong to componentj.
binsizes — Size of each connected component
vector
Size of each connected component, returned as a vector.
binsizes(i) gives the number of elements in component
i. The length of binsizes is equal
to the number of connected components, max(bins).
More About
Weakly Connected Components
Two nodes belong to the same weakly connected component if there is a path connecting them (ignoring edge direction). There are no edges between two weakly connected components.
The concepts of strong and weak components apply only to directed graphs, as they are equivalent for undirected graphs.
Strongly Connected Components
Two nodes belong to the same strongly connected component if there are paths connecting them in both directions. There can be edges between two strongly connected components, but these connecting edges are never part of a cycle.
The bin numbers of strongly connected components are such that any edge connecting two components points from the component of smaller bin number to the component with a larger bin number.
The concepts of strong and weak components apply only to directed graphs, as they are equivalent for undirected graphs.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
The name-value argument
'OutputForm','cell'that specifies cell array output is not supported.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
Version History
Introduced in R2015b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)