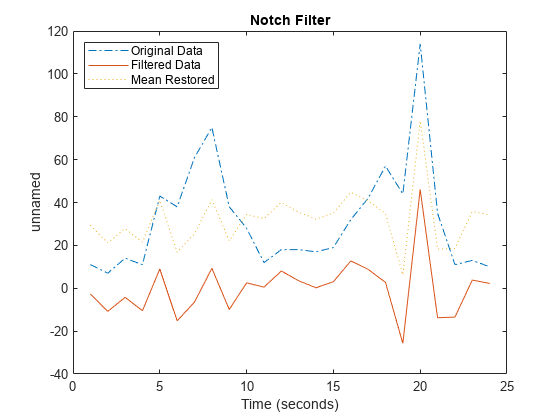
idealfilter
timeseries ideal filter
Syntax
Description
tsout = idealfilter(
applies an ideal (noncausal) filter of type tsin,interval,filtertype)filtertype to the
frequency intervals specified by interval for a
timeseries object tsin.
Ideal filters are noncausal, and the ends of the filter amplitude
are flat in the frequency domain. The data in ts must have zero
mean.
tsout = idealfilter(
optionally specifies the row or column indices of tsin,interval,filtertype,ind)tsin to apply
the filter to.
Examples
Input Arguments
Version History
Introduced before R2006a