Use Suboptimal Solution in Fast MPC Applications
This example shows how to guarantee the worst-case execution time of an MPC controller in real-time applications by using the suboptimal solution returned by the optimization solver.
What is a Suboptimal Solution?
Model predictive control (MPC) solves a quadratic programming (QP) problem at each control interval. The built-in QP solver uses an iterative active-set algorithm that is efficient for MPC applications. However, when constraints are present, there is no way to predict how many solver iterations are required to find an optimal solution. Also, in real-time applications, the number of iterations can change dramatically from one control interval to the next. In such cases, the worst-case execution time can exceed the limit that is allowed on the hardware platform and determined by the controller sample time.
You can guarantee the worst-case execution time for your MPC controller by applying a suboptimal solution after the number of optimization iterations exceeds a specified maximum value. To set the worst-case execution time, first determine the time needed for a single optimization iteration by experimenting with your controller under nominal conditions. Then, set a small upper bound on the number of iterations per control interval.
By default, when the maximum number of iterations is reached, an MPC controller does not use the suboptimal solution. Instead, the controller sets an error flag (status = 0) and freezes its output. Often, the solution available in earlier iterations is good enough, but requires refinement to find an optimal solution, which leads to many additional iterations.
This example shows how to configure your MPC controller to use the suboptimal solution. The suboptimal solution is a feasible solution available at the final iteration (modified, if necessary, to satisfy any hard constraints on the manipulated variables). To determine whether the suboptimal solution provides acceptable control performance for your application, run simulations across your operating range.
Define Plant Model
The plant model is a stable randomly generated state-space system. It has 10 states, 3 manipulated variables (MV), and 3 outputs (OV).
rng(1234); nX = 10; nOV = 3; nMV = 3; Plant = rss(nX,nOV,nMV); Plant.d = 0; Ts = 0.1;
Design MPC Controller with Constraints on MVs and OVs
Create an MPC controller with default values for all controller parameters except the constraints. Specify constraints on both the manipulated and output variables.
verbosity = mpcverbosity('off'); % Temporarily disable command line messages. mpcobj = mpc(Plant, Ts); for i = 1:nMV mpcobj.MV(i).Min = -1.0; mpcobj.MV(i).Max = 1.0; end for i = 1:nOV mpcobj.OV(i).Min = -1.0; mpcobj.OV(i).Max = 1.0; end
Simultaneous constraints on both manipulated and output variables require a relatively large number of QP iterations to determine the optimal control sequence.
Simulate in MATLAB with Random Output Disturbances
First, simulate the MPC controller using the optimal solution in each control interval. To focus on only output disturbance rejection performance, set the output reference values to zero.
T = 5; N = T/Ts + 1; r = zeros(1,nOV); SimOptions = mpcsimopt(); SimOptions.OutputNoise = 3*randn(N,nOV); [y,t,u,~,~,~,status] = sim(mpcobj,N,r,[],SimOptions);
Plot the number of iterations used in each control interval.
figure stairs(status) hold on title('Number of Iterations')

The largest number of iterations is 21, and the average is 5.8 iterations.
Create an MPC controller with the same settings, but configure it to use the suboptimal solution.
mpcobjSub = mpcobj; mpcobjSub.Optimizer.UseSuboptimalSolution = true;
Reduce the maximum number of iterations for the default active-set QP solver to a small number.
mpcobjSub.Optimizer.ActiveSetOptions.MaxIterations = 3;
Simulate the second controller with the same output disturbance sequence.
[ySub,tSub,uSub,~,~,~,statusSub] = sim(mpcobjSub,N,r,[],SimOptions);
Plot the number of iterations used in each control interval on the same plot. For any control interval in which the maximum number of iterations is reached, statusSub is zero. Before plotting the result, set the number of iterations for these intervals to 3.
statusSub(statusSub == 0) = 3; stairs(statusSub) legend('optimal','suboptimal')

The largest number of iterations is now 3, and the average is 2.8 iterations.
Compare the performance of the two controllers. When the suboptimal solution is used, there is no significant deterioration in control performance compared to the optimal solution.
figure for ct=1:3 subplot(3,1,ct) plot(t,y(:,ct),t,ySub(:,ct)) end subplot(3,1,1) title('Outputs') legend('optimal','suboptimal')

For a real-time application, as long as each solver iteration takes less than 30 milliseconds on the hardware, the worst-case execution time does not exceed the controller sample time (0.1 seconds). In general, it is safe to assume that the execution time used by each iteration is more or less a constant.
Simulate in Simulink with Random Output Disturbances
Open the Simulink model containing both controllers and simulate it.
Model = 'mpc_SuboptimalSolution';
open_system(Model)
sim(Model)

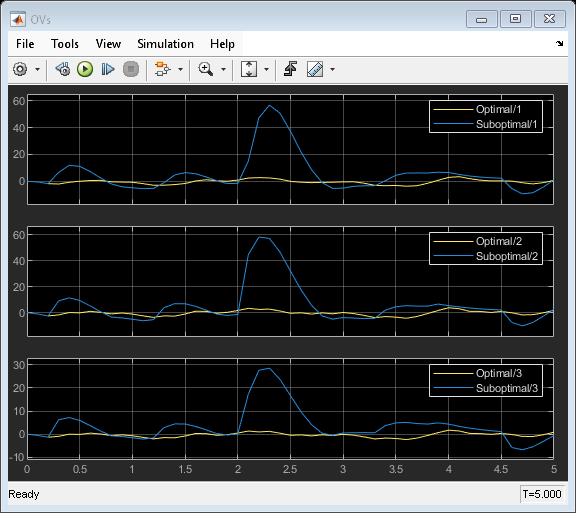

As in the command-line simulation, the average number of QP iterations per control interval decreased without significantly affecting control performance.
mpcverbosity(verbosity); % Enable command line messages.
bdclose(Model)
