Measure Transition Risk for Loan Portfolios with Respect to Climate Scenarios
This example shows the effect of transition risk on portfolios of loans from two banks given three different climate scenarios. Potentially, climate change is a large structural change affecting the economy and the financial system. Clear physical risks are associated with climate change, including increases in the global average temperature and an increased frequency and severity of extreme weather events. These events could result in significant macroeconomic and financial system impacts. In addition to physical risk, another type of risk called transition risk arises from changes in policy and new technologies, such as the growth of renewable energy.
Several countries around the globe are working on projects to understand and model different climate policies. For example, these climate initiatives are examples of projects investigating economic risk:
LIMITS (Low climate IMpact scenarios and the Implications of required Tight emission control Strategies) was a research effort that included twelve partners from Europe, China, India, Japan, and the United States. The main objectives of the project were: (a) to provide an assessment of the emissions reductions strategies at a world level for the major global economies, and (b) to disseminate scientific knowledge for climate and energy policy. [4]
The Bank of Canada launched a pilot project with the Office of the Superintendent of Financial Institutions.The goal of the pilot project was to understand risks to the economy and the financial system related to climate change. This work included developing a set of climate transition scenarios relevant to Canada that explore pathways consistent with achieving certain climate targets. [1]
The Massachusetts Institute of Technology (MIT) developed the Economic Projection and Policy Analysis (EPPA) model that is part of the MIT Integrated Global Systems Model (IGSM) that represents the human systems. EPPA is a recursive-dynamic multi-regional general equilibrium model of the world economy, which is built on the Global Trade Analysis Project (GTAP) data set and additional data for the greenhouse gas and urban gas emissions. IGSM is designed to develop projections of economic growth and anthropogenic emissions of greenhouse related gases and aerosols. [3]
The Climate Integrated Assessment Models Explorer repository contains a set of tools to explore different data sets hosted by the IIASA Energy program (ENE). This repositiory contains an example that computes changes to multiple bank loan portfolios as a result of climate shocks. [2]
This example follows an approach of Monasterolo [5] to develop a novel climate stress-test methodology for portfolios of loans to energy infrastructure projects and follows the workflow:
Obtain Climate Scenario Data
This example uses climate scenarios developed by MIT in collaboration with the Bank of Canada. The scenarios are described as:
Baseline (2019 policies) — baseline scenario consistent with climate policies in place at the end of 2019
Below 2°C Immediate — immediate policy action scenario to limit average global warming to below 2°C
Below 2°C Delayed — delayed policy action scenario to limit average global warming to below 2°C
Net-Zero 2050 (1.5°C) — more ambitious immediate policy action scenario to limit average global warming to 1.5°C that includes current net-zero commitments by some countries
The Climate Transition Scenario data is provided by the Bank of Canada and is available free of charge at www.bankofcanada.ca. [1]
The data is converted to a MAT file and is loaded from BankOfCanadaClimateScenarioData.mat.
Compute Market Share Shocks
Load the data file for the Climate Transition Scenario provided by the Bank of Canada. This data set contains energy information of different sectors for various geographies around the world. The CL_VARIABLE column in the data set contains both input information used to model the different climate scenarios, as well as, output information of energy usage. This example focuses on the different forms of primary energy, that is: bioenergy, coal, gas, hydro, nuclear, oil, and renewables (wind and solar). The example computes the market shares for each of the different energy forms and uses this information to calculate climate shocks. The different geographies in the data set are Africa, Canada, China, Europe, India, Japan, the United States, and the rest of the world.
load BankOfCanadaClimateScenarioData.mat
head(ClimateTransitionScenarioData) k CL_GEOGRAPHY CL_SECTOR CL_VARIABLE CL_UNIT CL_SCENARIO CL_YEAR CL_VALUE
_ ____________ _________ _______________________________ ___________________ ________________________ _______ ________
1 Canada National Carbon price US$2014/tCO2e Baseline (2019 policies) 2020 12.106
2 Canada National Carbon price US$2014/tCO2e Below 2°C immediate 2020 12.106
3 Canada National Emissions | total GHG (scope 1) Million tonnes CO2e Baseline (2019 policies) 2020 781.04
4 Canada National Emissions | total GHG (scope 1) Million tonnes CO2e Below 2°C immediate 2020 781.04
5 Canada National Input price | Coal Index (2014 = 1) Baseline (2019 policies) 2020 1.2875
6 Canada National Input price | Coal Index (2014 = 1) Below 2°C immediate 2020 1.2875
7 Canada National Input price | Crops Index (2014 = 1) Baseline (2019 policies) 2020 1.0031
8 Canada National Input price | Crops Index (2014 = 1) Below 2°C immediate 2020 1.0031
Trim and preprocess the original data set for what is required for this example.
% This example uses only the Primary Energy variables to compute market % shares for different geographies. VariableSubset = {'Primary Energy | Bioenergy', 'Primary Energy | Coal', 'Primary Energy | Gas', ... 'Primary Energy | Hydro', 'Primary Energy | Nuclear', 'Primary Energy | Oil', ... 'Primary Energy | Renewables (wind&solar)', 'Primary Energy | Total'}; ClimateTransitionScenarioData = ClimateTransitionScenarioData(ismember(ClimateTransitionScenarioData.CL_VARIABLE, VariableSubset),:); % Remove columns 'k','CL_SECTOR' and 'CL_UNIT' and then sort the rows. ClimateTransitionScenarioData = removevars(ClimateTransitionScenarioData,{'k','CL_SECTOR','CL_UNIT'}); ClimateTransitionScenarioData = sortrows(ClimateTransitionScenarioData); % Pull market share data out according to climate scenario. baseline = ClimateTransitionScenarioData(ismember(ClimateTransitionScenarioData.CL_SCENARIO, 'Baseline (2019 policies)'),:); b2delayed = ClimateTransitionScenarioData(ismember(ClimateTransitionScenarioData.CL_SCENARIO, 'Below 2°C delayed'),:); b2immediate = ClimateTransitionScenarioData(ismember(ClimateTransitionScenarioData.CL_SCENARIO, 'Below 2°C immediate'),:); netzero2050 = ClimateTransitionScenarioData(ismember(ClimateTransitionScenarioData.CL_SCENARIO, 'Net-zero 2050 (1.5°C)'),:); % Compile all the scenarios into one data set. MarketShareData = baseline; MarketShareData = removevars(MarketShareData, "CL_SCENARIO"); MarketShareData.Properties.VariableNames(4) = "BASELINE"; MarketShareData.BELOW_2C_IMMEDIATE = b2immediate.CL_VALUE; MarketShareData.BELOW_2C_DELAYED = b2delayed.CL_VALUE; MarketShareData.NETZERO_2050 = netzero2050.CL_VALUE; head(MarketShareData)
CL_GEOGRAPHY CL_VARIABLE CL_YEAR BASELINE BELOW_2C_IMMEDIATE BELOW_2C_DELAYED NETZERO_2050
____________ __________________________ _______ ________ __________________ ________________ ____________
Africa Primary Energy | Bioenergy 2020 15.502 15.502 15.502 15.502
Africa Primary Energy | Bioenergy 2025 15.302 15.302 15.302 15.302
Africa Primary Energy | Bioenergy 2030 15.221 15.203 15.221 15.292
Africa Primary Energy | Bioenergy 2035 15.072 15.042 15.084 15.218
Africa Primary Energy | Bioenergy 2040 15.016 15.055 15.23 15.631
Africa Primary Energy | Bioenergy 2045 14.249 14.273 14.652 14.993
Africa Primary Energy | Bioenergy 2050 13.591 14 14.645 14.607
Africa Primary Energy | Coal 2020 4.5909 4.5909 4.5909 4.5909
Select the geography and subsector, and then compute the market share. By default, in this example, a coal project in China is selected.
Geography ="China"; Sector =
"Coal"; SectorFullName = "Primary Energy | " + Sector; BaseSector = "Primary Energy | Total"; Years = (2020:5:2050)'; GeographyData = MarketShareData(MarketShareData.CL_GEOGRAPHY == Geography, :); MarketShare = GeographyData{GeographyData.CL_VARIABLE == SectorFullName, 4:7} ./ GeographyData{GeographyData.CL_VARIABLE == BaseSector, 4:7} * 100;
Plot the market shares for different climate scenarios. For the coal sector in China, the baseline scenario shows a drop in market share. However, this drop is accelerates in each of the three climate scenarios. The Below 2C Delayed scenario coincides with the baseline up until 2030, after which there is a sudden fall in market share, whereas the other two scenarios (Below 2C Immediate and Net-Zero 2050) lose market share more gradually until 2050.
figure; msPlot = plot(Years, MarketShare, 'LineWidth',2); grid on set(msPlot, {'LineStyle'}, {'-';'--';':';'-.'}) legend("Baseline", "Below 2C Immediate", "Below 2C Delayed", "Net-Zero 2050 (1.5C)", 'Location','best'); xlim([2020 2050]) ylabel('Market Share (%)') xlabel('Year') title(Sector + " Market Share in " + Geography)

Compute shocks for all climate scenarios.
Shocks = (MarketShare(:,2:4) - MarketShare(:,1))./MarketShare(:,1)*100;
Plot the shocks for different scenarios. For the default coal sector in China, the Below 2C Immediate and the Net-Zero 2050 scenarios have a gradual negative market share shock over time. However, the Below 2C Delayed scenario shows no market share shock until 2030, and then there is a sudden drop until 2050.
figure; shp = plot(Years, Shocks, 'LineWidth',2); grid on set(shp, {'LineStyle'}, {'--';':';'-.'}) xlabel('Year') ylabel('Market Share Shocks (%)') xlim([2020 2050]) legend("Below 2C Immediate", "Below 2C Delayed", "Net-Zero 2050 (1.5C)", 'Location','best'); title(Sector + " Market Share Shocks in " + Geography);

Obtain Loan Portfolio Data
This example uses a second data set (ClimateLoanPortfolioData.mat) for a loan portfolio. This data set contains simulated loan data of two fictitious banks: Bank 1 and Bank 2. The portfolio of loans are from different geographies and sectors. The example uses the face value of the loans to compute the change in reserves that a bank has to allocate when a climate shock occurs.
The distribution of loans for the two banks, by energy sector, is:
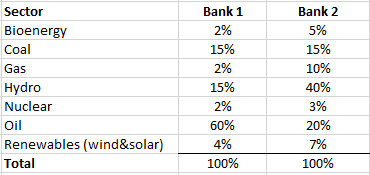
Generate histograms to show the distribution of loans, by region and sector, for the two simulated banks.
load ClimateLoanPortfolioData LoanPortfolioDataBank1 = ClimateLoanPortfolioData(ClimateLoanPortfolioData.Bank=='Bank1',:); LoanPortfolioDataBank2 = ClimateLoanPortfolioData(ClimateLoanPortfolioData.Bank=='Bank2',:); [CountsRegion1, BinsRegion1] = histcounts(LoanPortfolioDataBank1.BorrowerRegion); [CountsSector1, BinsSector1] = histcounts(LoanPortfolioDataBank1.BorrowerSector); [CountsRegion2, BinsRegion2] = histcounts(LoanPortfolioDataBank2.BorrowerRegion); [CountsSector2, BinsSector2] = histcounts(LoanPortfolioDataBank2.BorrowerSector); figure tiledlayout(2,1) nexttile barh(categorical(BinsRegion1), [CountsRegion1; CountsRegion2]); xlabel('Loans') ylabel('Regions') title('Distribution of Regions') legend({'Bank 1', 'Bank 2'},'Location','best') nexttile barh(categorical(BinsSector1), [CountsSector1; CountsSector2]); xlabel('Loans') ylabel('Sectors') title('Distribution of Sectors') legend({'Bank 1', 'Bank 2'},'Location','best')

Bank 1 is heavily invested in fossil fuel projects (primarily oil) and Bank 2 is invested in green energy projects (primarily hydro). Regarding the distribution of projects across geographies, both banks are similar, with a larger number of projects in developing regions like China, India, and Africa.
Create Valuation Framework for Loan Contracts Subject to Climate Policy Shocks
Using the same notation as in Monasterolo [5], consider a bank i endowed with a portfolio of investments in a set of projects through loan contracts. Each loan is represented by a distinct value j. The goal is to carry out a valuation of this loan portfolio that accounts for climate policy shocks. The methodology assumes an underlying structural model that is similar to the Merton model (see mertonmodel). The valuation model includes three time steps: . Time step denotes the time at which the valuation is carried out, denotes the time at which the climate policy shock potentially occurs, and denotes the maturity of the loan .
The valuation of bank i's loan portfolio is written as
.
Consider an approach based on the expected value of the loan
,
where is the face value of the loan, is the recovery rate on the loan contract, and is the probability, based on the information available at time that the borrower, j, defaults on the loan at maturity .
Therefore, the expected value of the loan is the face value of the loan minus the reserves or provisions that need to be set aside by the bank for that loan .
At time t* the occurrence of a climate policy shock implies that the economy switches from a business-as-usual scenario characterized by no climate policy (B) to scenario P, where the market shares of some economic sectors are affected. This change in default probability implies a proportional change in the expected value of the loan
,
where denotes the difference of the default probability going from scenario B to P.
This change is the negative of the change in provisions for the loan. That is, if the value goes down, it is due to an increase in provisions driven by the change in probability.
Assume that the policy shock impacts the borrower's balance sheet, and thus the expected value of the loan. Let denote the primary energy value for sector , region , scenario , climate model , and time . Let denote the total energy value for region , scenario , climate model , and time . We define the corresponding market share as
.
The same definitions apply to scenario . We define a market share shock, , as
.
Assume that a relative change in the market share of borrower 's sector within the geographic region , denoted by , implies a proportional relative change in 's profitability. Also, because the net worth is the integral of profits over one period of time, the relative change in net worth and profit coincide. Therefore, it is equivalent to assume that a relative change in net worth is proportional to the relative shock in market share
,
where denotes the elasticity of profitability with respect to market share. Monasterolo [5] assumes a value of constant and equal to 1 (typical empirical values range from 0.2 and 0.6).
Another assumption by Monasterolo [5] is that the probability distribution of the shocks on the borrower's asset side follows a uniform distribution with support and mean , for a given model , region, and sector. Therefore, the change in default probability is expressed as
.
The change in expected value of the loan, conditional to a change from scenario B to scenario P becomes:
.
Summing the projects j in the portfolio, you obtain the total change in loan value:
.
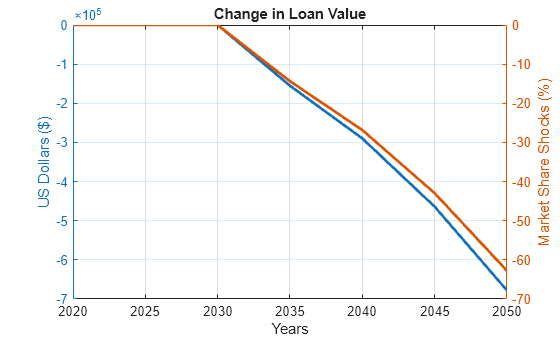
This example computes the change in value for one loan. By default, the 12th row of the data set is selected, which is an oil project in the United States for Bank 1. you can choose another loan by using the Loan slider. You can also select a different ClimateScenario from the three available scenarios. By default, the Below Delayed scenario is selected.
Loan =12; ClimateScenario =
2; Geography = string(ClimateLoanPortfolioData{Loan,'BorrowerRegion'}); Sector = string(ClimateLoanPortfolioData{Loan,'BorrowerSector'}); LoanID = ClimateLoanPortfolioData{Loan,'LoanID'}; FaceValueOfLoan = ClimateLoanPortfolioData{Loan,"FaceValue"}; SectorFullName = "Primary Energy | " + Sector;
Compute the value of the selected Loan.
disp(ClimateLoanPortfolioData(Loan,:));
LoanID BorrowerCreditRating LoanType Bank InterestRate InterestType BorrowerID BorrowerRegion BorrowerSector OriginationDate MaturityDate FaceValue FairValue
___________ ____________________ ________ _____ ____________ ____________ ______________ ______________ ______________ _______________ ____________ _________ __________
"786801JSP" A2 Term Bank1 0.028 Fixed "SI14476197XI" United States Oil 31-Oct-2019 30-Nov-2031 6e+06 5.7948e+06
You can modify the recovery rate , as well as, . By default, and . A normal range of is from 0.2 to 0.6.
Following the Monasterolo [5] discussion in appendix I, set to correspond to the assumption that the magnitude of the initial net worth and width of the distribution of the idiosyncratic shocks are comparable. You can adjust the EjDeltaRatio value using the slider.
RecoveryRate =0.4; Chi =
0.3; EjDeltaRatio =
1; TargetYear =
4; GeographyData = MarketShareData(MarketShareData.CL_GEOGRAPHY == Geography, :); MarketShare = GeographyData{GeographyData.CL_VARIABLE == SectorFullName, 4:7} ./ GeographyData{GeographyData.CL_VARIABLE == BaseSector, 4:7} * 100; Shocks = (MarketShare(:,2:4) - MarketShare(:,1))./MarketShare(:,1)*100; ChangeInDefaultProbability = -EjDeltaRatio.*Chi.*(Shocks(:,ClimateScenario)/100); ChangeInValue = -FaceValueOfLoan.*(1-RecoveryRate).*ChangeInDefaultProbability;
The change in value of a loan is directly translated into a change in the reserves that need to be allocated by the bank for that particular loan.
disp("The change in value of the loan in the selected climate scenario and target year = $" + num2str(ChangeInValue(TargetYear)));The change in value of the loan in the selected climate scenario and target year = $-155161.6488
% Plot change in value of loan over time superimposed over corresponding % shock. f = figure; ax = axes(f); yyaxis(ax, 'left') plot(Years, ChangeInValue, 'LineWidth', 2) xlabel('Years'); ylabel('US Dollars ($)') yyaxis(ax, 'right') plot(Years, Shocks(:, ClimateScenario), 'LineWidth', 2); ylabel('Market Share Shocks (%)'); title('Change in Loan Value'); grid on
Compute Change in Value of Entire Portfolio of Loans
For each of the two banks, Bank 1 and Bank 2, compute the total change in loan value of the entire portfolio of loans for each climate scenario. You can do this by summing up the changes in values of each individual loan.
% For each of the region and sector pairs, compute the market shocks for % all scenarios and store these values. MarketShocks = struct(); Bank1Combos = unique(table(LoanPortfolioDataBank1.BorrowerRegion, LoanPortfolioDataBank1.BorrowerSector,'VariableNames',{'Region','Sector'}),'rows'); Bank2Combos = unique(table(LoanPortfolioDataBank2.BorrowerRegion, LoanPortfolioDataBank2.BorrowerSector,'VariableNames',{'Region','Sector'}),'rows'); TotalCombos = union(Bank1Combos, Bank2Combos); for i = 1:height(TotalCombos) Region = string(TotalCombos.Region(i)); Sector = string(TotalCombos.Sector(i)); SectorFullName = "Primary Energy | " + Sector; GeographyData = MarketShareData(MarketShareData.CL_GEOGRAPHY == Region, :); MarketShare = GeographyData{GeographyData.CL_VARIABLE == SectorFullName, 4:7} ./ GeographyData{GeographyData.CL_VARIABLE == BaseSector, 4:7} * 100; Shocks = (MarketShare(:,2:4) - MarketShare(:,1))./MarketShare(:,1)*100; if Sector == "Renewables (wind&solar)" SectorSplit = strsplit(Sector); Sector = SectorSplit(1); end MarketShocks.(strrep(Region,' ','')).(strrep(Sector,' ','')) = Shocks; end
Create a table containing the values of each loan, for each bank, for each climate scenario, and for each target year. Use the same model parameter values for simplicity. However, you can change these parameters for different issuers.
RecoveryRate =0.46; Chi =
0.3; EjDeltaRatio =
1; LoanValues = ClimateLoanPortfolioData; LoanValues = removevars(LoanValues,{'LoanType','BorrowerCreditRating','InterestRate','InterestType','BorrowerID','OriginationDate','MaturityDate','FairValue'}); LoanValues = repelem(LoanValues, 7, 1); LoanValues.Year = repmat([2020; 2025; 2030; 2035; 2040; 2045; 2050], 1000, 1); LoanValues.Below2CImmediate = zeros(7000, 1); LoanValues.Below2CDelayed = zeros(7000, 1); LoanValues.NetZero2050 = zeros(7000, 1); for i = 1:7:height(LoanValues) Region = string(LoanValues.BorrowerRegion(i)); Sector = string(LoanValues.BorrowerSector(i)); if Sector == "Renewables (wind&solar)" SectorSplit = strsplit(Sector); Sector = SectorSplit(1); end Value = LoanValues.FaceValue(i); ChangeInValue = Value.*(1-RecoveryRate).*EjDeltaRatio.*Chi.*(MarketShocks.(strrep(Region,' ','')).(strrep(Sector,' ',''))/100); LoanValues{i:i+6, {'Below2CImmediate','Below2CDelayed','NetZero2050'}} = ChangeInValue; end
Compare the change in portfolio values of the two banks, for each climate scenario, and for all target years.
TPVBank1 = zeros(length(Years),3); TPVBank2 = zeros(length(Years),3); for i = 1:length(Years) TBank1 = LoanValues((LoanValues.Bank == "Bank1") & (LoanValues.Year == Years(i)), :); TBank2 = LoanValues((LoanValues.Bank == "Bank2") & (LoanValues.Year == Years(i)), :); TPVBank1(i,:) = sum(TBank1{:,7:9}); TPVBank2(i,:) = sum(TBank2{:,7:9}); end figure; t = tiledlayout(3,1); nexttile plot(Years, [TPVBank1(:,1),TPVBank2(:,1)], 'LineWidth', 2) xlabel('Year'); ylabel('US Dollar ($)') title('Below 2C Immediate') grid on nexttile plot(Years, [TPVBank1(:,2),TPVBank2(:,2)], 'LineWidth', 2) xlabel('Year'); ylabel('US Dollar ($)') title('Below 2C Delayed') grid on nexttile plot(Years, [TPVBank1(:,3),TPVBank2(:,3)], 'LineWidth', 2) xlabel('Year'); ylabel('US Dollar ($)') title('Net-Zero 2050') leg = legend({'Bank1','Bank2'}); leg.Layout.Tile = 'south'; grid on title(t,'Change in Portfolio Value');

Considering that Bank 1 is weighted towards fossil fuels and Bank 2 is weighted toward green energy, the portfolio value of Bank 1 decreases over time, while the portfolio value of Bank 2 increases over time for each climate scenario.
From a reserves standpoint, the provisions of Bank 2 steadily increase over time and those of Bank 1 decrease over time.
Compute Distribution of Changes in Loan Portfolio Values
The Compute Change in Value of Entire Portfolio of Loans section illustrated the aggregate changes to the portfolio value. This section focuses on the entire distribution of value changes for particular climate scenarios.
Select the bank, climate scenario, and target year to compute the quartiles of the change in portfolio values.
Bank ="Bank1"; ClimateScenario =
2; TargetYear =
"2050"; NewTable = LoanValues((LoanValues.Bank == Bank) & (LoanValues.Year == str2double(TargetYear)), :);
Plot the histogram of the change in loan values for the selected bank and climate scenario. Based on the default selection of Bank 1 under the Below 2C Delayed climate scenario for the target year 2050, you see that the distribution of the change in loan values has a long right tail and most of the frequency is below zero. This change occurs because Bank 1 has more projects focusing on fossil fuels, which lose market share, and thus value over time under the Below 2C Delayed climate scenario.
f = figure;
h = histogram(NewTable{:,6+ClimateScenario});
h.Parent.XLabel.String = 'Change in Loan Value';
h.Parent.YLabel.String = 'Counts';
h.Parent.Title.String = 'Histogram of Change in Loan Values';
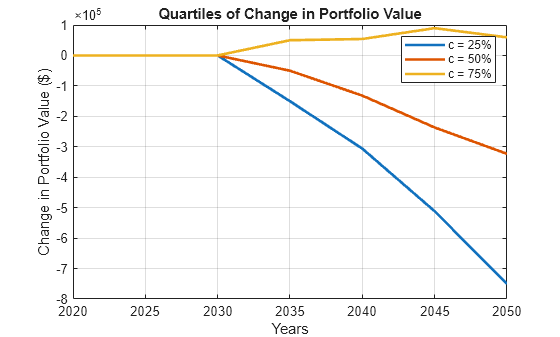
Compute and plot the quartiles of the changes in portfolio values over time for the selected bank.
PLV = zeros(length(Years),3); for i = 1:length(Years) t = LoanValues((LoanValues.Bank == Bank) & (LoanValues.Year == Years(i)), :); PLV(i,1) = prctile(t{:,6+ClimateScenario}, 25); PLV(i,2) = prctile(t{:,6+ClimateScenario}, 50); PLV(i,3) = prctile(t{:,6+ClimateScenario}, 75); end figure; plot(Years, PLV, 'LineWidth', 2) xlabel('Years'); ylabel('Change in Portfolio Value ($)') title('Quartiles of Change in Portfolio Value') legend({'c = 25%','c = 50%','c = 75%'}) grid on
To compute some standard metrics of risk such as the Value-at-Risk (VaR) of the portfolio, you need to know the joint probaility distribution of the idiosyncratic shocks and the probability of occurrence of climate policy shocks. In the absence of these estimations, Monasterolo [5] defines a project-level climate VaR as the value such that, conditional to the same climate policy shock for all n loans, the fraction of loans leading to losses higher than the VaR equals the confidence level c
.
This project-level climate VaR metric is a percentile of the distribution of value changes for the portfolio.
ConfidenceLevel =1; ProjVaR = -prctile(NewTable{:,6+ClimateScenario}, ConfidenceLevel); disp("The project-level climate VaR at the " + ConfidenceLevel + "% confidence level = $" + num2str(ProjVaR));
The project-level climate VaR at the 1% confidence level = $1453621.915
Plot a graph of distributions of changes in loan values for each target year and for a given scenario and bank. Use the kernel smoothing function estimate for univariate data. The estimate is based on a normal kernel function and is evaluated at equally spaced points that cover the range of the data.
[F1Bank1, Xi1Bank1] = ksdensity(TBank1.Below2CImmediate); [F1Bank2, Xi1Bank2] = ksdensity(TBank2.Below2CImmediate); [F2Bank1, Xi2Bank1] = ksdensity(TBank1.Below2CDelayed); [F2Bank2, Xi2Bank2] = ksdensity(TBank2.Below2CDelayed); [F3Bank1, Xi3Bank1] = ksdensity(TBank1.NetZero2050); [F3Bank2, Xi3Bank2] = ksdensity(TBank2.NetZero2050); figure; t = tiledlayout(3,1); ax1 = nexttile; plot(Xi1Bank1, F1Bank1, 'LineWidth', 1.5) hold on plot(Xi1Bank2, F1Bank2, 'LineWidth', 1.5) ax1.Title.String = "Below 2C Immediate"; xlabel('US Dollar ($)') ylabel('pdf') grid on ax2 = nexttile; plot(Xi2Bank1, F2Bank1, 'LineWidth', 1.5) hold on plot(Xi2Bank2, F2Bank2, 'LineWidth', 1.5) ax2.Title.String = "Below 2C Delayed"; xlabel('US Dollar ($)') ylabel('pdf') grid on ax3 = nexttile; plot(Xi3Bank1, F3Bank1, 'LineWidth', 1.5) hold on plot(Xi3Bank2, F3Bank2, 'LineWidth', 1.5) leg = legend("Bank 1","Bank 2"); leg.Layout.Tile = 'south'; ax3.Title.String = "Net-Zero 2050"; xlabel('US Dollar ($)') ylabel('pdf') grid on title(t,'Distribution of Changes in Loan Values');

Conclusion
Following the work Monasterolo [5], this example demonstrates how the market shares of different energy sectors in different geographies change under specific climate scenarios. The market share changes are converted into market share shocks and you can use these shocks to compute the change in value of a portfolio of loans. Using this approach, you can model additional climate scenarios and then apply the Monasterolo [5] methodology. In addition, you can use this approach to value a portfolio of other assets such as bonds.
References
[1] Bank of Canada Climate Transition Scenario Data and pilot project available at https://www.bankofcanada.ca/2022/01/climate-transition-scenario-data/ and https://www.bankofcanada.ca/wp-content/uploads/2021/11/BoC-OSFI-Using-Scenario-Analysis-to-Assess-Climate-Transition-Risk.pdf.
[2] Climate IAM Explorer available at https://github.com/mathworks/Climate-IAM-Explorer.
[3] EPPA Model Structure available at https://globalchange.mit.edu/research/research-tools/eppa and https://globalchange.mit.edu/research/research-tools/human-system-model.
[4] LIMITS information available at https://tntcat.iiasa.ac.at/LIMITSDB/dsd?Action=htmlpage&page=about.
[5] Monasterolo, I., Zheng, Jiani I., and S. Battiston. "Climate Transition Risk and Development Finance: An Assessment of China's Overseas Energy Investments Portfolio." China and the World Economy. 26, 6(116–142), 2018. Available at https://doi.org/10.1111/cwe.12264.
