Overview of Claims Estimation Methods for Non-Life Insurance
The ability to accurately estimate unpaid claims is important to insurers. Unlike companies in other sectors, insurers might not know the exact earnings during a financial reporting period until many years later. Insurance companies take in insurance premiums on a regular basis and pay out claims when events occur. In order to maximize profits, an insurance company must accurately estimate how much will be paid out on existing claims in the future. If the estimate for unpaid claims is too low, the insurance company will become insolvent. Conversely, if the estimate is too high, then the claims reserve capital of the insurance company could have been invested elsewhere or reinvested in the business [1].
Risk Management Toolbox™ supports four claims estimation methods for actuaries to use for estimating unpaid claims:
Workflow to Estimate Unpaid Claims
For the different claims estimation methods, the basic workflow follows.
Create a development triangle with insurance claims data using
developmentTriangle. The claims data can be for either reported claims or paid claims. You can plot reported claims usingclaimsPlot.Use the development triangle to compute link ratios using
linkRatios. You can plot link ratios usinglinkRatiosPlot.Use the development triangle link ratio for reported claims or paid claims to compute the link ratio averages with
linkRatioAverages.Use
ultimateClaimsto compute the projected ultimate claims based on the link ratio averages for either reported claims or unpaid claims.Using the projected ultimate claims for both the reported and paid development triangles, use any of the following to compute incurred-but-not-reported (IBNR) values and the total unpaid claims estimates:
Chain ladder method — Create a
chainLadderobject with development triangles for reported and paid claims, generate the IBNR values usingibnr, and compute the unpaid claims estimation withunpaidClaims.Expected claims method — Create an
expectedClaimsobject with development triangles for reported and paid claims as well as the earned premium. By default, the initial claims are calculated as the average of the reported ultimate claims and the paid ultimate claims. However, you can specify custom values for the initial claims. Similar to the chain ladder method, you can compute IBNR values usingibnrand the unpaid claims estimates withunpaidClaims.Bornhuetter-Ferguson method — Create a
bornhuetterFergusonobject with development triangles for reported and paid claims as well as initial expected claims values, generate IBNR usingibnr, and compute the unpaid claims estimation withunpaidClaims.Cape Cod method — Create a
capeCodobject with development triangles for reported and paid claims as well as initial expected claims values, generate IBNR usingibnr, and compute the unpaid claims estimation withunpaidClaims.
Estimation of Ultimate Claims Using Development Triangles
One characteristic of Development Triangles is that the ultimate claims are estimated from recorded values assuming that the development of future claims resembles that in prior years — the past is indicative of the future.
The steps for development triangles are demonstrated using simulated data:
Use
developmentTriangleto generate the reported claims in what is called a development triangle, where there is one row for each origin year and the columns depict how the claims develop over time.
Use
linkRatiosto calculate the age-to-age factors. These factors are also known as report-to-report factors or link ratios. The link ratios measure the change in recorded claims from one valuation date to the next. The standard naming convention is starting month-ending month. For example, the age-to-age factor for the 12-month period to the 24-month period is often referred to as the 12-24 factor.To calculate the age-to-age factors for the 12-24 period, divide the claims as of 24 months by the claims as of 12 months. Thus, the triangle of age-to-age factors has one less row and one less column than the original data triangle.
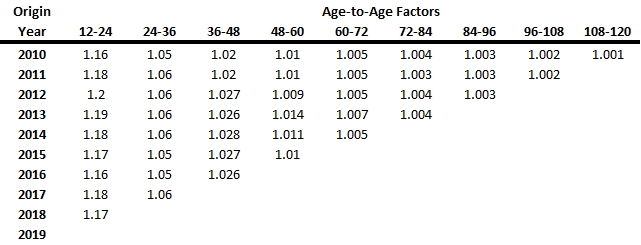
After calculating the age-to-age factors, use
linkRatioAveragesto calculate the averages of the age-to-age factors. Actuaries use a wide variety of averages for age-to-age factors. Some of the common ones are the simple average, medial average, geometric average, and volume-weighted average.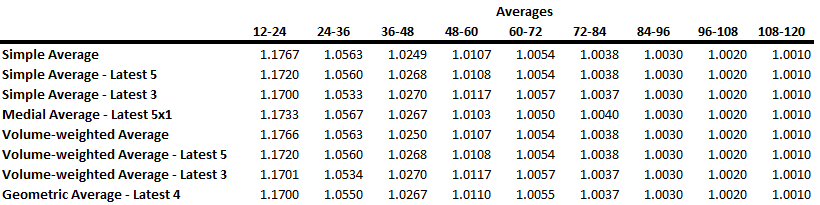
Use
cdfSummaryto obtain the cumulative claim development factors (CDF), which are calculated by successive multiplications beginning with the tail factor and the oldest age-to-age factor. The cumulative claim development factor projects the total growth over the remaining valuations.
All of the previous steps apply to the reported claims. In order to calculate the unpaid claims estimates, you need the paid claims as well as the reported claims. Use
developmentTriangleto generate the development triangle for paid claims.
Similar to the reported claims development triangle, you use the paid claims develop triangle to calculate link ratios, average link ratios, and then you can select one link ratio and calculate the cumulative development factors.
Use
ultimateClaimsto project the ultimate claims. The ultimate claims are equal to the product of the latest valuation of claims and the appropriate cumulative claim development factors. The projected ultimate claims are displayed for both the reported claims and the paid claims.
After calculating the projected ultimate claims, use a
chainLadder,expectedClaims, orbornhuetterFergusonmethod for estimating the unpaid claims.
Estimation of Unpaid Claims Using Chain Ladder Method
The chain ladder method requires the Development Triangles for reported and paid claims. The chain ladder method assumes that you can predict future claims activity for a given origin year (accident year, policy year, report year, and so on) based on historical claims activity to date for that origin year. The primary assumption of this method is that the reporting and payment of future claims resembles the patterns observed in the past.
In addition, the chain ladder method requires a large volume of historical claims experience. It works best when the presence or absence of large claims does not greatly distort the data. If the volume of data is not sufficient, large claims can greatly distort the age-to-age factors, the projections of ultimate claims, and the estimate of unpaid claims.
After calculating the projected ultimate claims using Development Triangles, create a
chainLadderobject based on the reported and paid Development Triangles in order to compute the unpaid claim estimates withunpaidClaims.Actuaries calculate the unpaid claims estimate as the difference between the projected ultimate claims and the actual paid claims. This value of the unpaid claim estimate represents total unpaid claims, including both the outstanding claims cases and the IBNR claims. To determine estimated IBNR values based on the chain ladder technique, subtract reported claims from the projected ultimate claims. Alternatively, you can use
ibnrto calculate the IBNR, which is equal to the estimate of total unpaid claims less the outstanding cases.
Estimation of Unpaid Claims Using Expected Claims Method
The key assumption of the expected claims method is that an actuary can better estimate unpaid claims based on an initial estimate rather than existing claims observed to date.
The expected claims method requires the Development Triangles for reported and paid claims as well as the earned premium. By default, the initial claims are calculated as the average of the reported ultimate claims and the paid ultimate claims. However, you can specify custom values for the initial claims. Using the initial claims, an actuary applies a claim ratio method, where ultimate claims for a development period are equal to a selected expected claim ratio multiplied by the earned premium. Using these calculated ultimate claims, the actuary can then compute the unpaid claims estimates.
Create an
expectedClaimsobject to calculate theultimateClaims.
Use the
expectedClaimsobject to calculate theunpaidClaims.
Estimation of Unpaid Claims Using Bornhuetter-Ferguson Method
The Bornhuetter-Ferguson method combines the chain ladder method and the expected claims method by splitting ultimate claims into two components, actual reported (or paid) claims and expected unreported (or unpaid) claims. As the claim matures over development periods, more weight is given to the actual claims and the expected claims become gradually less important.
The Bornhuetter-Ferguson method requires the Development Triangles for reported and paid claims as well as initial expected claims values. The Bornhuetter-Ferguson method calculates its own projected ultimate claims, different from those calculated in the Development Triangle object. Using these new projected ultimate claims, the unpaid claims estimates are computed.
Create a
bornhuetterFergusonobject to calculate theultimateClaims.
Use the
bornhuetterFergusonobject to calculate theunpaidClaims.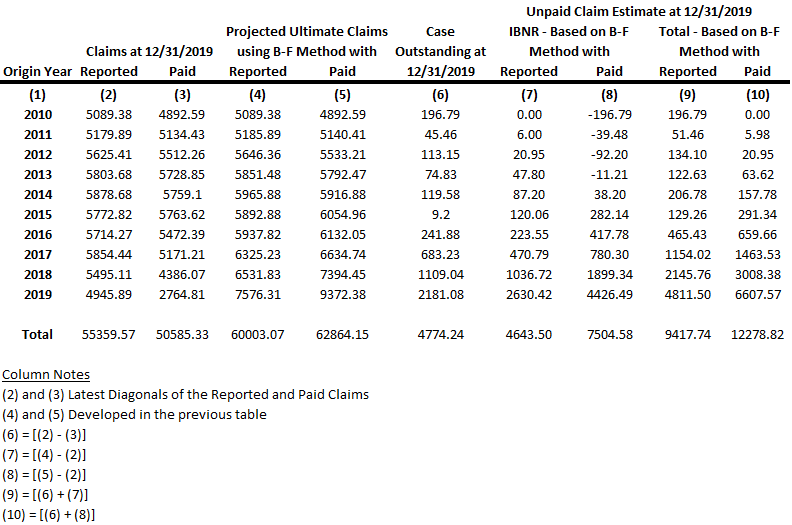
Estimation of Unpaid Claims Using Cape Cod Method
As in the Bornhuetter-Ferguson technique, the Cape Cod technique splits ultimate claims into two components: actual reported (or paid) and expected unreported (or unpaid). As an accident year (or other time interval) matures, the actual reported claims replace the expected unreported claims and the initial expected claims assumption becomes gradually less important. The primary difference between the two methods is the derivation of the expected claim ratio. In the Cape Cod technique, the expected claim ratio is obtained from the reported claims experience instead of an independent and often judgmental selection as in the Bornhuetter-Ferguson technique.
The Cape Cod technique requires the Development Triangles for reported and paid claims as well as the earned premium. The key assumption of the Cape Cod technique is that unreported claims will develop based on expected claims, which are derived using reported (or paid) claims and earned premium. Both the Cape Cod and Bornhuetter-Ferguson methods differ from the development method where the primary assumption is that unreported claims will develop based on reported claims to date (not expected claims).
Create a
capeCodobject to calculate theultimateClaims.
Use the
capeCodobject to calculate theunpaidClaims.
References
[1] Friedland, Jacqueline. "Estimating Unpaid Claims using Basic Techniques." Arlington, VA: Casualty Actuarial Society, 2010.
[2] Wüthrich, Mario, and Michael Merz. Stochastic Claims Reserving Methods in Insurance. Hoboken, NJ: Wiley, 2008.
See Also
developmentTriangle | chainLadder | expectedClaims | bornhuetterFerguson | capeCod
