chebwin
Chebyshev window
Description
Examples
Input Arguments
Output Arguments
Tips
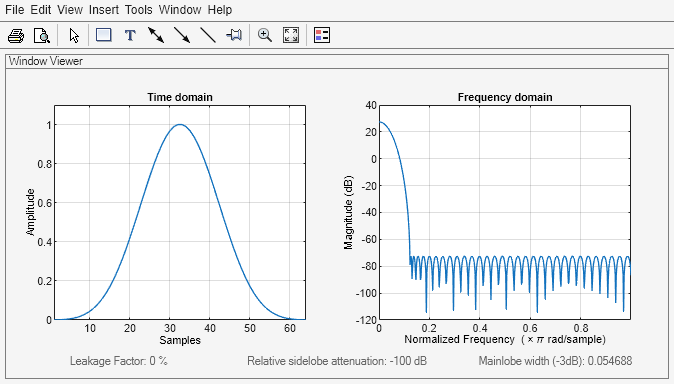
An artifact of the equiripple design method used in chebwin is the
presence of impulses at the endpoints of the time-domain response. The impulses are due to the
constant-level sidelobes in the frequency domain. The magnitude of the impulses are on the
order of the size of the spectral sidelobes. If the sidelobes are large, the effect at the
endpoints may be significant. For more information on this effect, see [2].
The equivalent noise bandwidth of a Chebyshev window does not grow monotonically with increasing sidelobe attenuation when the attenuation is smaller than about 45 dB. For spectral analysis, use larger sidelobe attenuation values, or, if you need to work with small attenuations, use a Kaiser window.
References
[1] Digital Signal Processing Committee of the IEEE Acoustics, Speech, and Signal Processing Society, eds. Programs for Digital Signal Processing. New York: IEEE Press, 1979, program 5.2.
[2] harris, fredric j. Multirate Signal Processing for Communication Systems. Upper Saddle River, NJ: Prentice Hall PTR, 2004, pp. 60–64.
Extended Capabilities
Version History
Introduced before R2006a