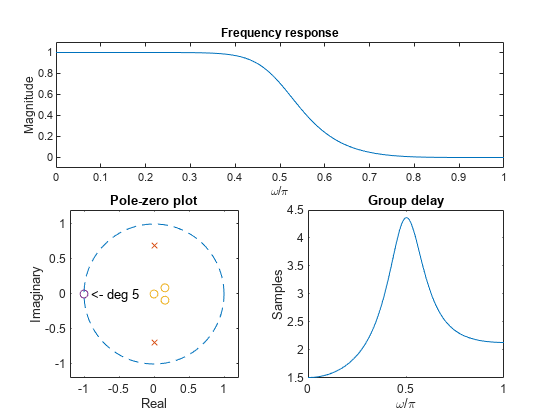
maxflat
Generalized digital Butterworth filter design
Syntax
Description
[___] = maxflat(
specifies the option to display the filter design as a table, plot, or both using
n,m,Wn,designflag)designflag. You can use any of the output combinations from previous
syntaxes.
Examples
Input Arguments
Output Arguments
References
[1] Selesnick, Ivan W., and C. Sidney Burrus. “Generalized Digital Butterworth Filter Design.” IEEE® Transactions on Signal Processing 46, no. 6, (June 1998): 1688–94.
Extended Capabilities
Version History
Introduced before R2006a