Signal Analyzer
Visualize and compare multiple signals and spectra
Description
The Signal Analyzer app is an interactive tool for visualizing, preprocessing, measuring, analyzing, and comparing signals in the time domain, in the frequency domain, and in the time-frequency domain. Using the app, you can:
Easily access all the signals in the MATLAB® workspace
Fill missing data (since R2024a); smooth, filter, resample, detrend, denoise, extract, and edit signals without leaving the app
Add and apply custom preprocessing functions
Play audio signals (since R2024a)
Visualize and compare multiple waveform, spectrum, persistence, spectrogram, and scalogram representations of signals simultaneously
Measure data and signal statistics
The Signal Analyzer app provides a way to work with many signals of varying durations at the same time and in the same view.
For more information, see Using Signal Analyzer App.
More
You need a Wavelet Toolbox™ license to use the scalogram view and to apply wavelet denoising to signals.
Open the Signal Analyzer App
MATLAB Toolstrip: On the Apps tab, under Signal Processing and Communications, click the app icon.
MATLAB command prompt: Enter
signalAnalyzer.
Examples
Find and Fill Missing Data in Audio File
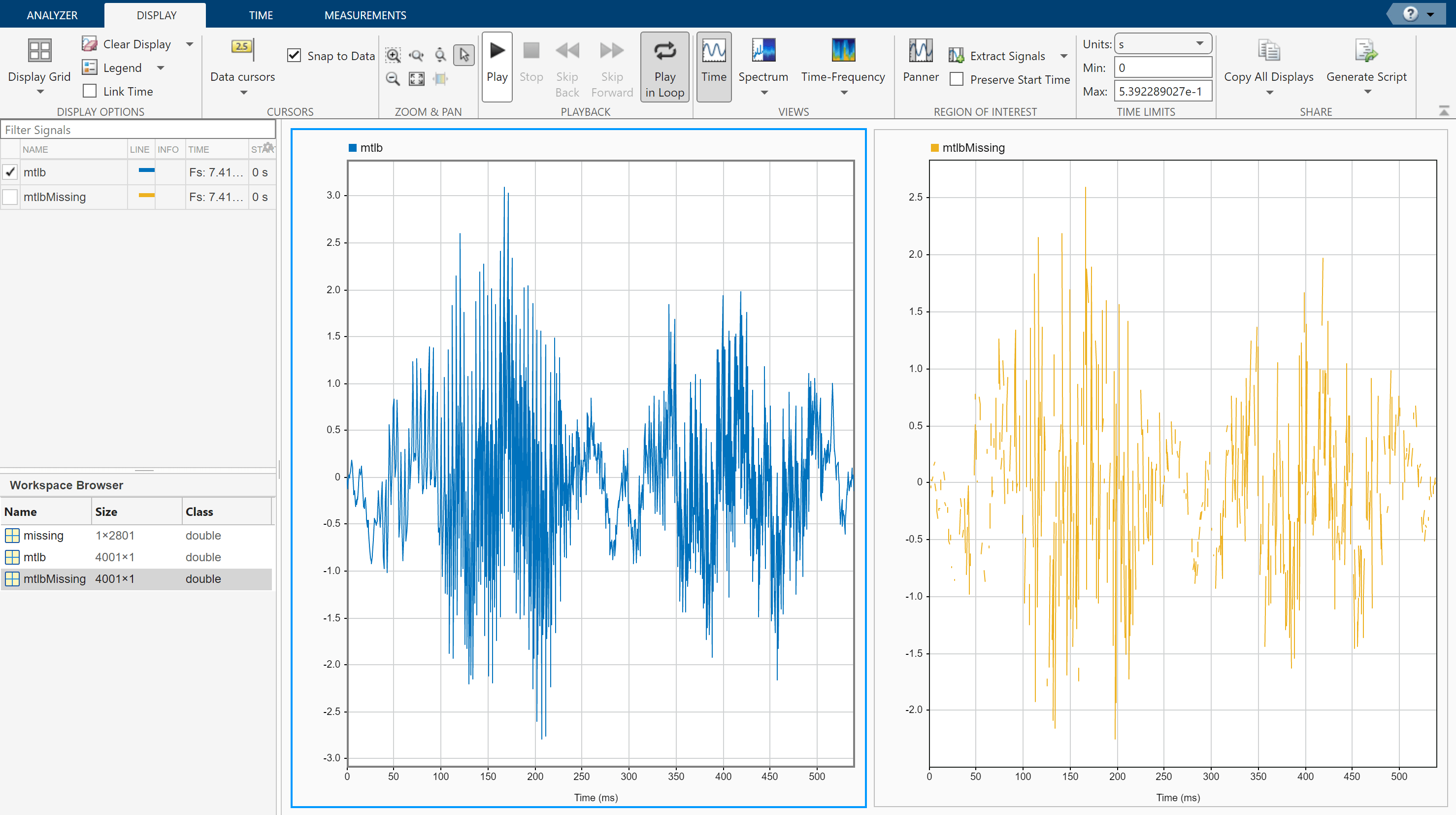
Load a speech signal sampled at . The file contains a recording of a female voice saying the word "MATLAB®."
load mtlbTo simulate a situation where 70% of the audio data is missing, randomly assigns NaN values to the signal.
rng(2024) numToReplace = round(length(mtlb) * 0.70); missing = randperm(length(mtlb), numToReplace); mtlbMissing = mtlb; mtlbMissing(missing) = NaN;
Open Signal Analyzer and drag the mtlb and mtlbMissing from the Workspace Browser to the Signal table. On the Analyzer tab, with the signals selected in the Signal table, click Time Values and select Sample Rate and Start Time. Specify Sample Rate as Fs Hz and Start Time as 0 s. Click Display Grid to create two side-by-side displays. Plot mtlb in the left display and mtlbMissing in the right display. To hear the mtlb audio signal, select it and click Play in the Playback section of the toolstrip under the Display tab. To repeat the signal, select Play in Loop before playing.
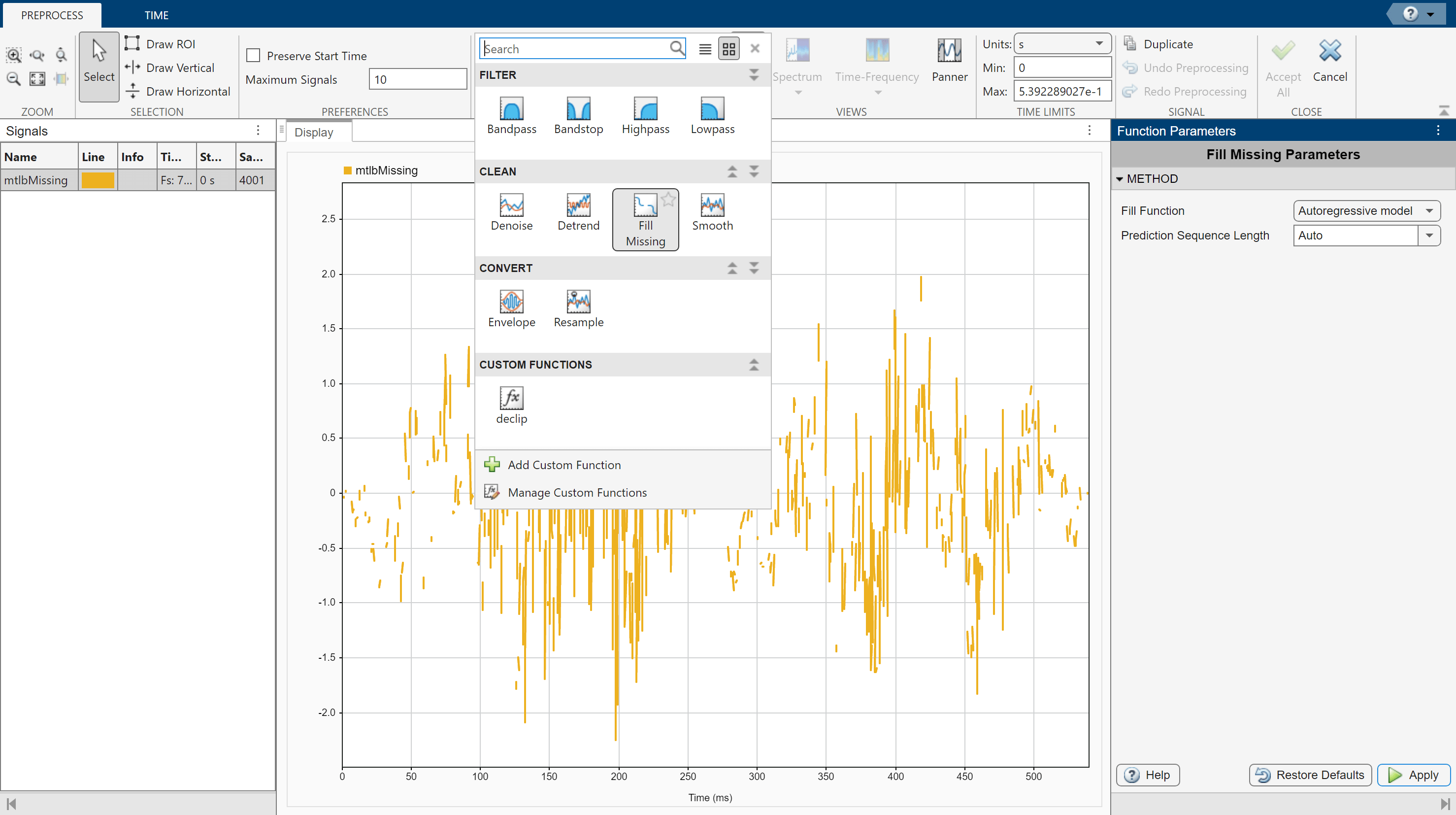
Select the signal with missing data and click Preprocess under the Analyzer tab to enter the preprocessing mode, then choose Fill Missing from the list of preprocessing options. Use the Function Parameters panel to adjust the Fill Missing parameters. Select Autoregressive model and click Apply to fill in the missing signal. Click Accept All to save the preprocessing results and exit the mode. For details on alternative fill functions, see fillmissing and fillgaps.
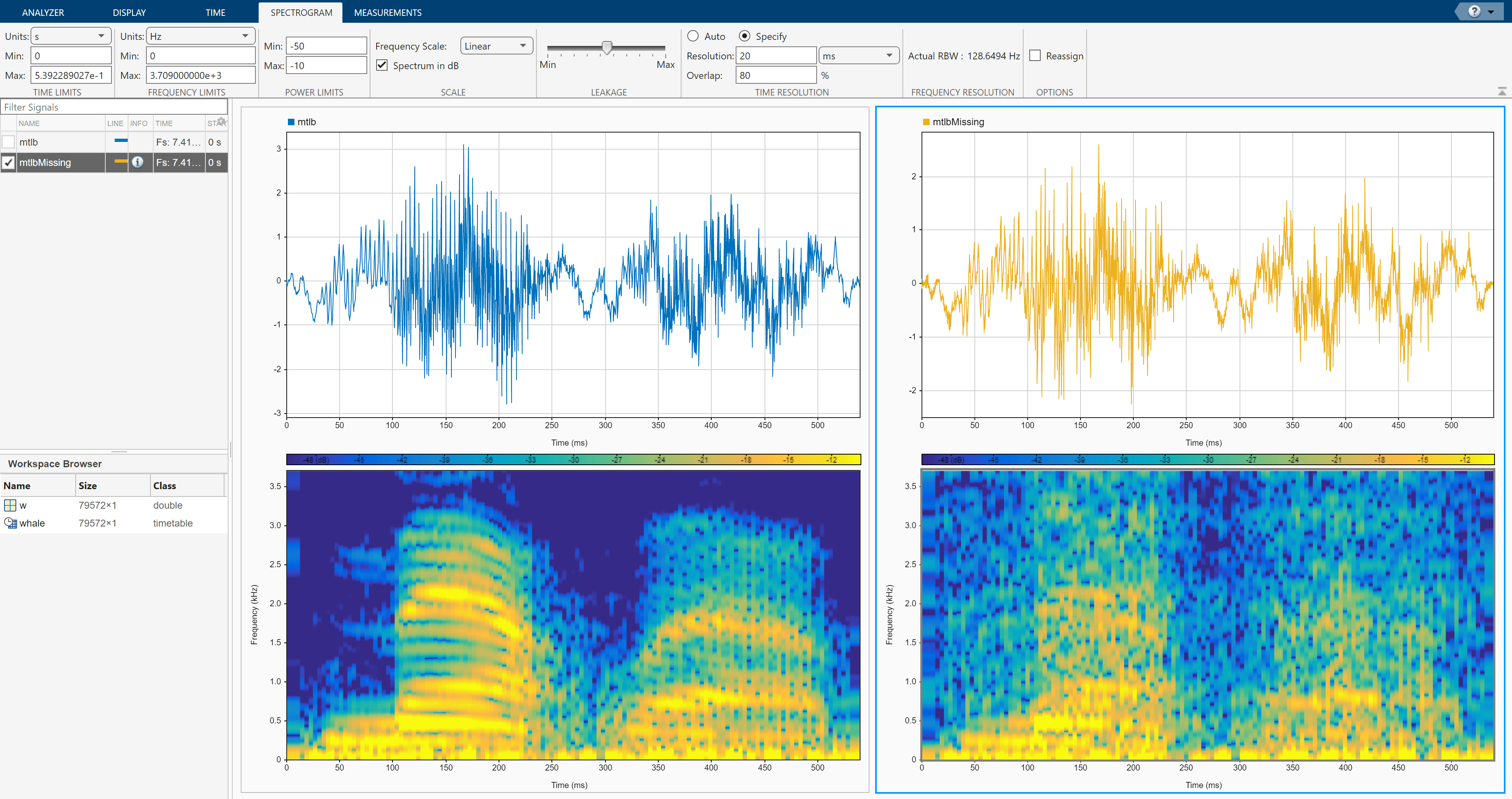
You can now play the filled signal using the Play button. To see the effects of fill missing on the spectrogram, click Time-Frequency on the Display tab. On the Spectrogram tab, specify a time resolution of 20 ms and 80% overlap between adjoining segments. Set the Power Limits to –50 dB and –10 dB. Click on the left display and repeat the steps.
Resolve Tones by Varying Window Leakage
You can adjust the spectral leakage of the analysis window to resolve sinusoids in Signal Analyzer.
Generate a two-channel signal sampled at 100 Hz for 2 seconds.
The first channel consists of a 20 Hz tone and a 21 Hz tone. Both tones have unit amplitude.
The second channel also has two tones. One tone has unit amplitude and a frequency of 20 Hz. The other tone has an amplitude of 1/100 and a frequency of 30 Hz.
fs = 100; t = (0:1/fs:2-1/fs)'; x = sin(2*pi*[20 20].*t)+[1 1/100].*sin(2*pi*[21 30].*t);
Embed the signal in white noise. Specify a signal-to-noise ratio of 40 dB.
x = x + randn(size(x)).*std(x)/db2mag(40);
Open Signal Analyzer and plot the signal. On the Analyzer tab, with the signal selected in the Signal table, click Time Values and select Sample Rate and Start Time. Specify Sample Rate as fs Hz and Start Time as 0 s. On the Display tab, click Spectrum to add a spectral plot to the display.
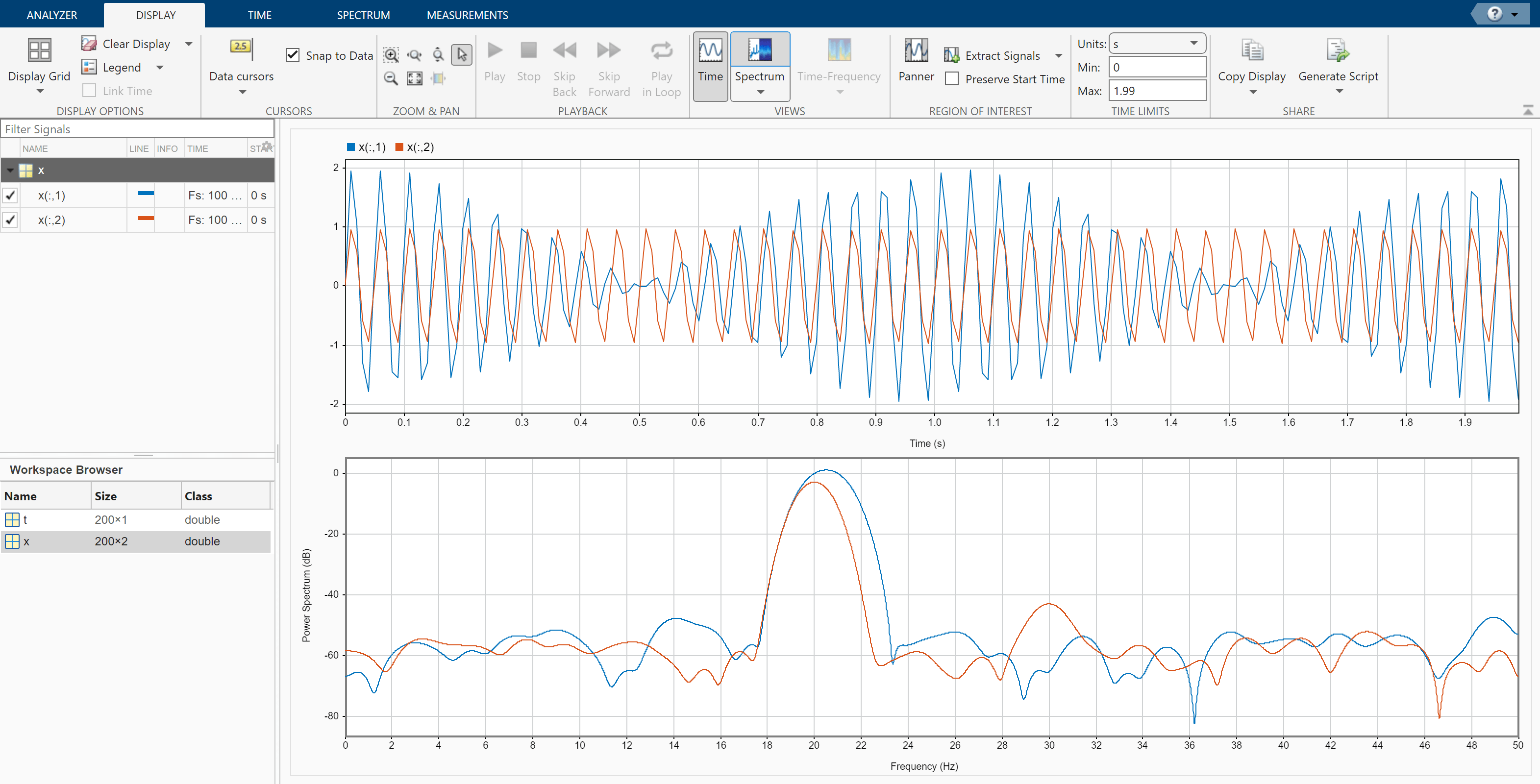
Click the Spectrum tab. The slider that controls the spectral leakage is in the middle position, corresponding to a resolution bandwidth of about 1.28 Hz. The two tones in the first channel are not resolved. The 30 Hz tone in the second channel is visible, despite being much weaker than the other one.
Increase the leakage so that the resolution bandwidth is approximately 0.83 Hz. The weak tone in the second channel is clearly resolved.
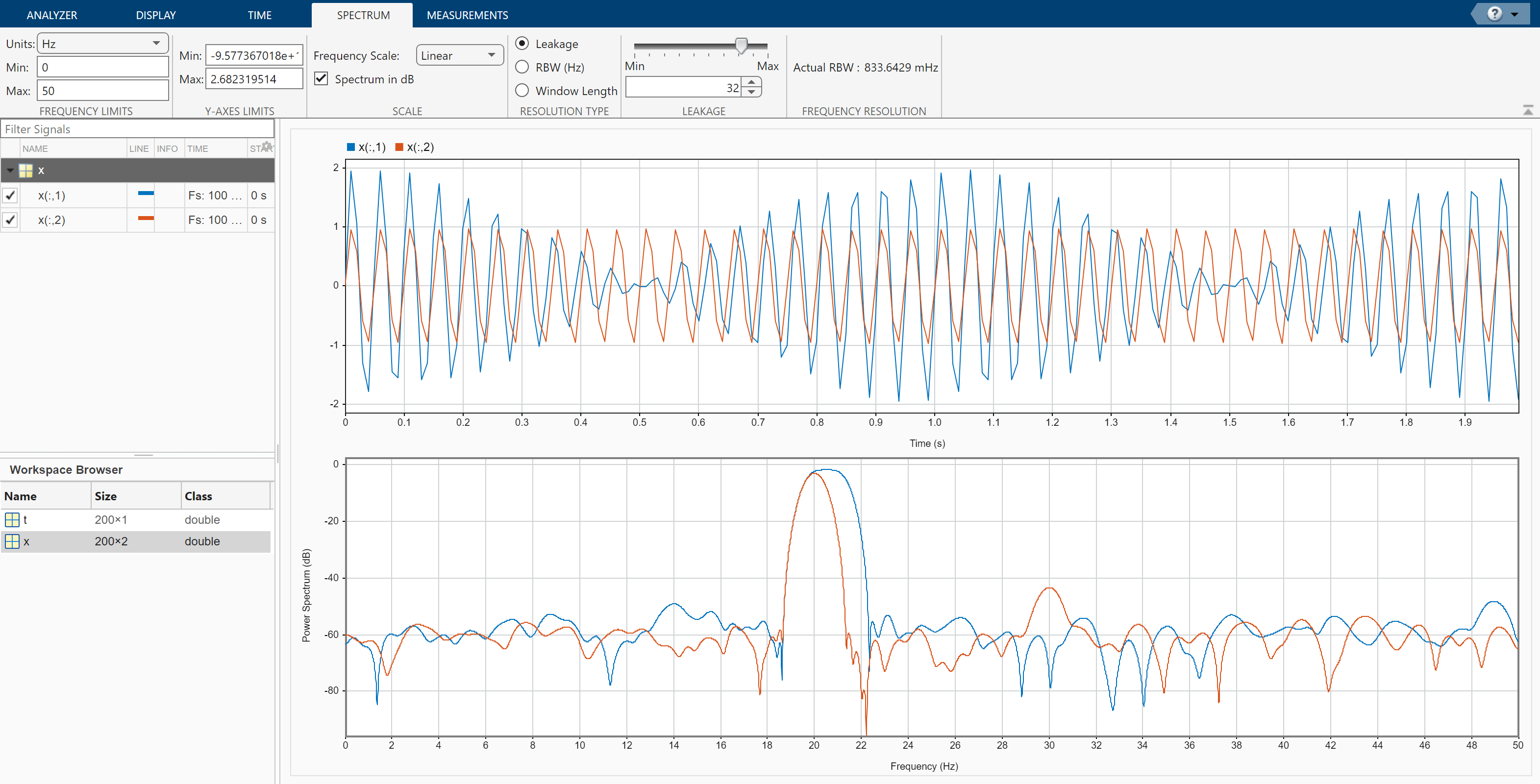
Move the slider to the maximum value. The resolution bandwidth is approximately 0.5 Hz. The two tones in the first channel are resolved. The weak tone in the second channel is masked by the large window sidelobes.
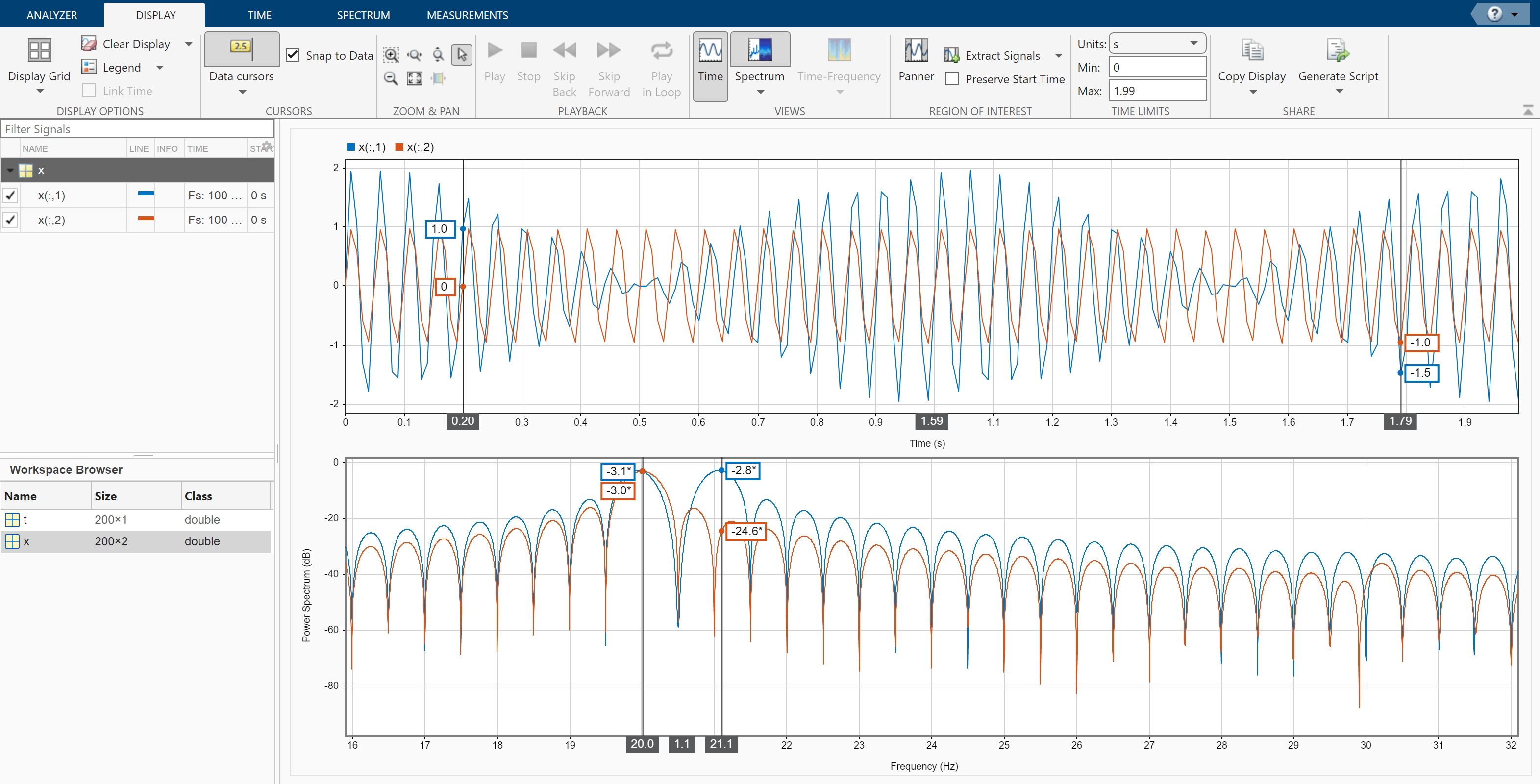
Click the Display tab. Use the horizontal zoom to magnify the frequency axis. Add two cursors to the display and drag the frequency-domain cursors to estimate the frequencies of the tones.
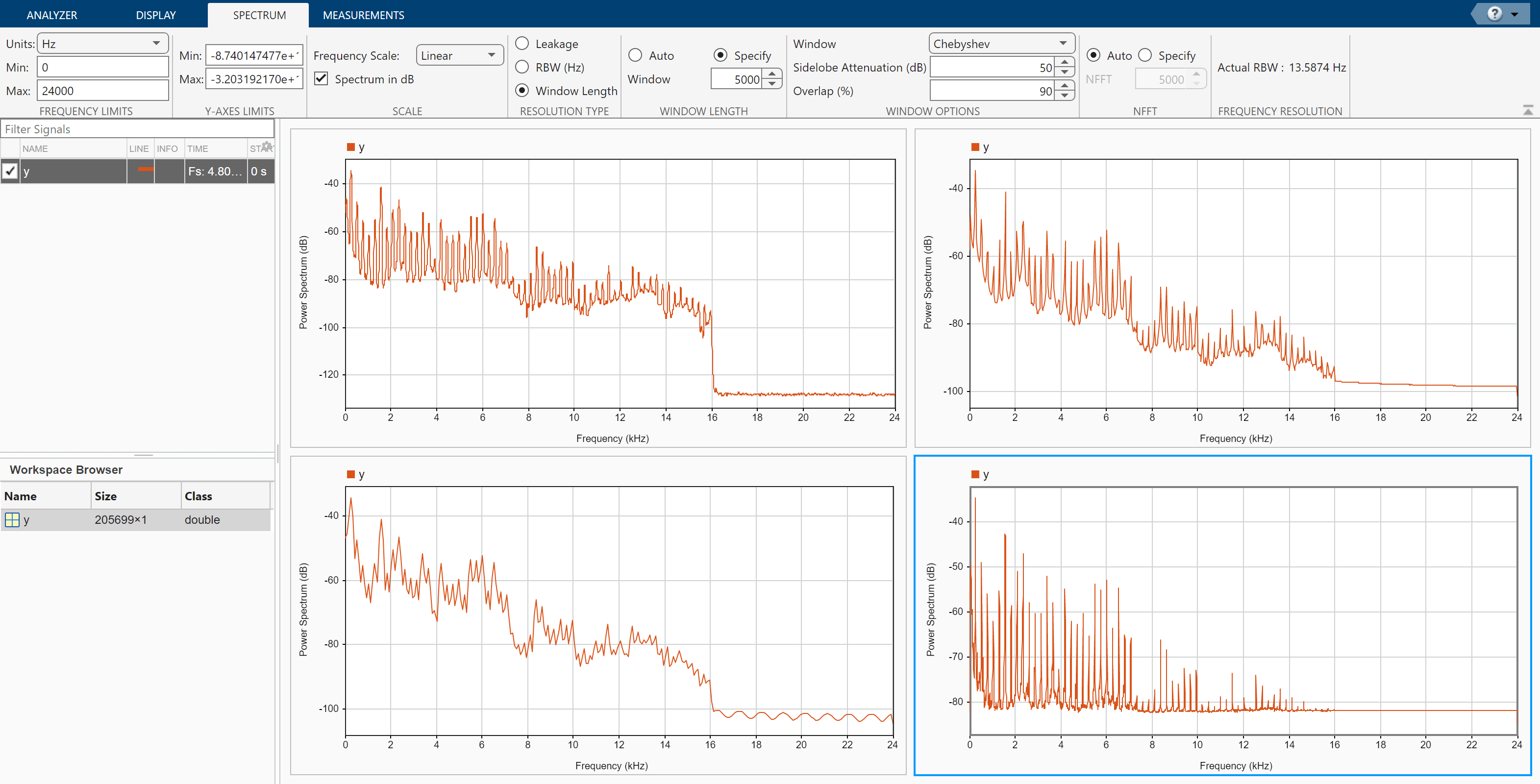
Compute Signal Spectrum Using Different Windows
Read an audio recording of an electronic toothbrush into MATLAB®. The signal is sampled at 48 kHz. The toothbrush turns on at about 1.75 seconds and stays on for approximately 2 seconds.
[y,fs] = audioread("toothbrush.m4a");Open Signal Analyzer and drag the signal from the Workspace Browser to the Signal table. Add time information to the signal by selecting it in the Signal table and clicking Time Values on the Analyzer tab. Select Sample Rate and Start Time and enter fs for the sample rate.
On the Display tab, click Display Grid to create a two-by-two grid of displays. Select each display, click Spectrum to add a spectrum view, and click Time to remove the time view. Drag the signal to all four displays.
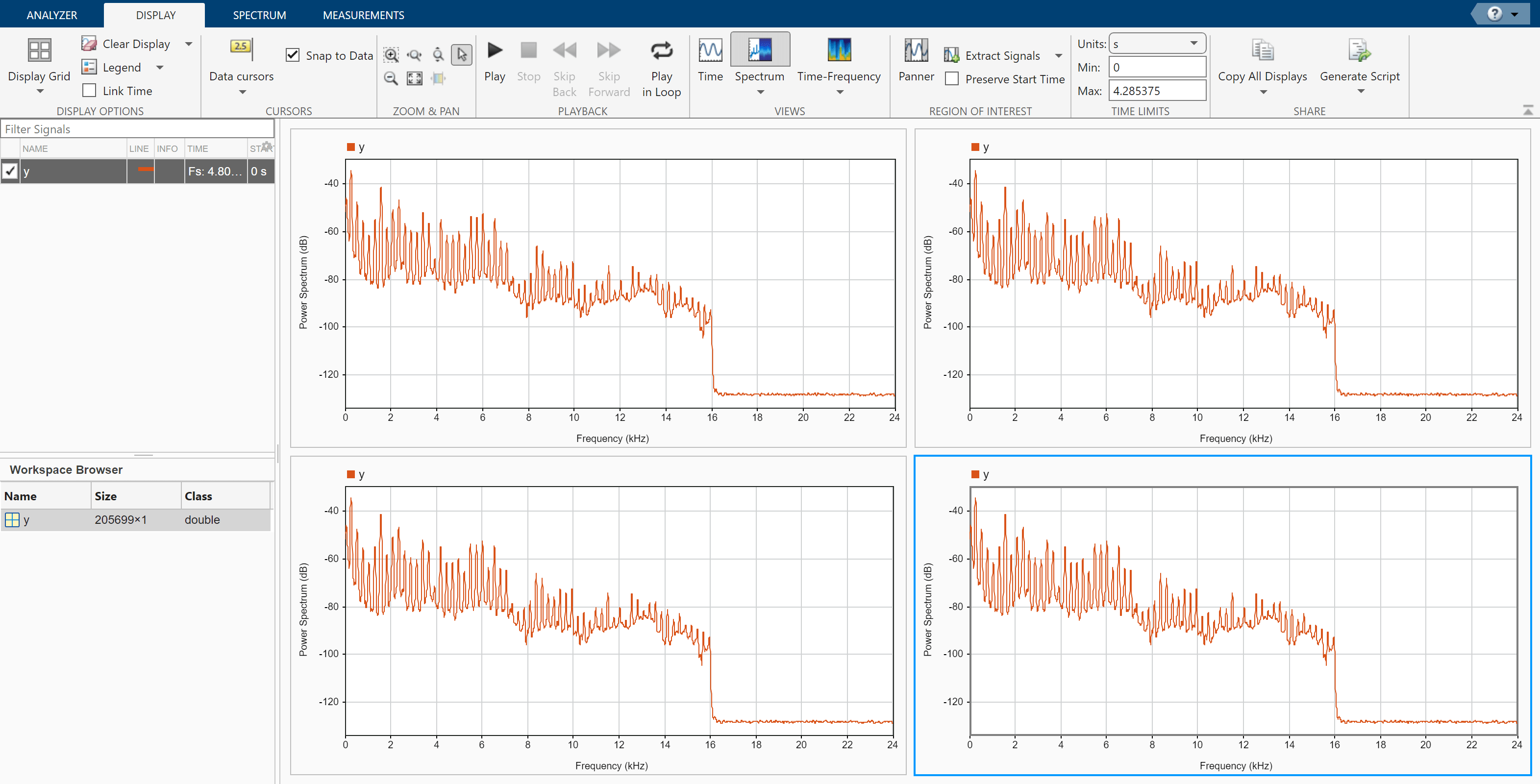
Click the Spectrum tab to modify the spectrum view in each display.
Click the top left display to select it. Move the Leakage slider until you get a leakage value of 32.
Click the top right display to select it. On the Resolution Type section, select Window Length. On the Window Length section, select Specify and specify a window length of 1500 samples. On the Window Options section, choose a
Rectangularwindow and specify an overlap percentage of 20.Click the bottom left display to select it. On the Resolution Type section, select Window Length. On the Window Length section, select Specify and specify a window length of 500 samples. On the Window Options section, choose a
Hammingwindow and specify an overlap percentage of 50. On the NFFT section, specify 550 discrete Fourier transform points.Click the bottom right display to select it. On the Resolution Type section, select Window Length. On the Window Length section, select Specify and specify a window length of 5000 samples. On the Window Options section, choose a
Chebyshevwindow and specify a sidelobe attenuation of 50 dB and an overlap percentage of 90.
You can see that some views show higher resolution but higher leakage, while other views have lower leakage but at the expense of resolution.
Related Examples
- Extract Voices from Music Signal
- Modulation and Demodulation Using Complex Envelope
- Find and Track Ridges Using Reassigned Spectrogram
- Declip Saturated Signals Using Your Own Function
- Compute Envelope Spectrum of Vibration Signal
- Find Delay Between Correlated Signals
- Find Interference Using Persistence Spectrum
- Denoise Noisy Doppler Signal
- Resample and Filter a Nonuniformly Sampled Signal
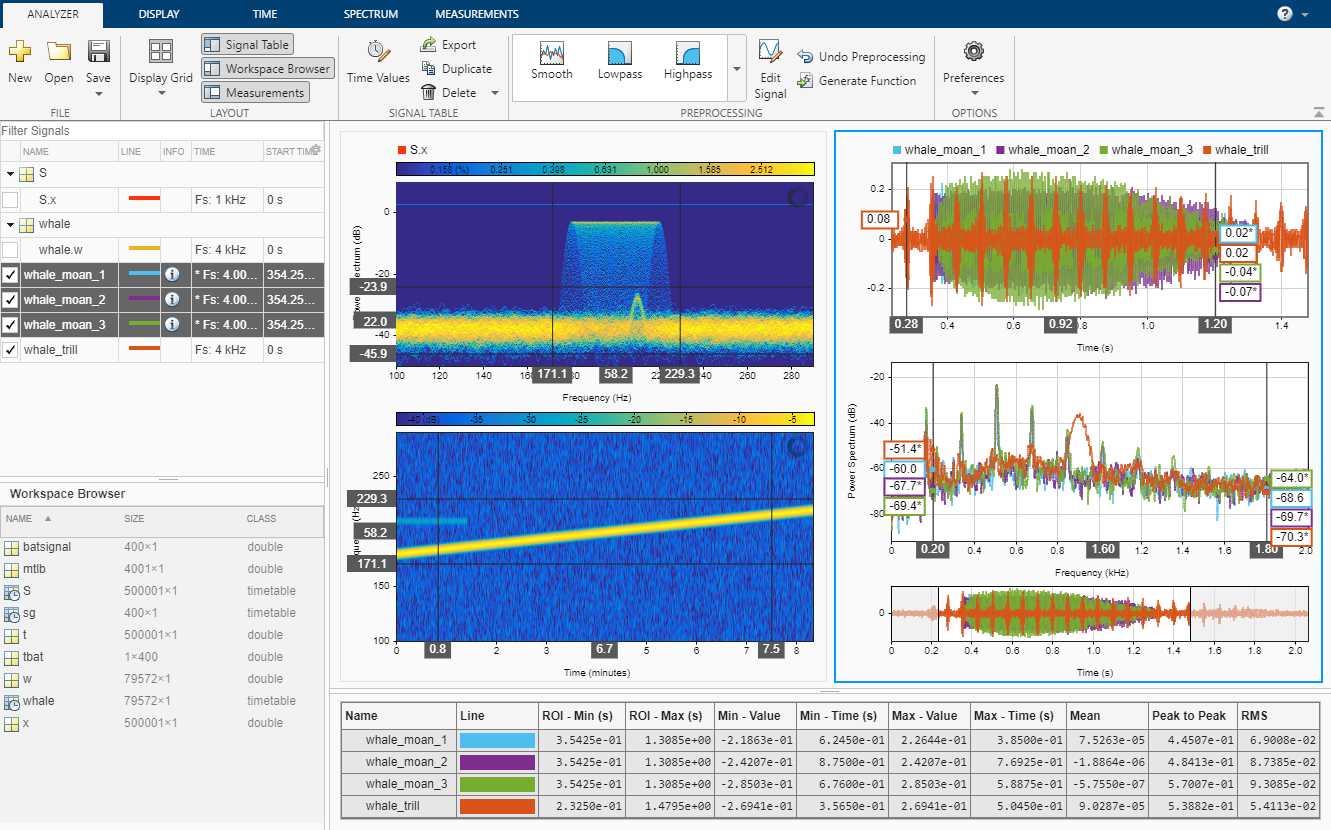
- Extract Regions of Interest from Whale Song
Programmatic Use
signalAnalyzer
signalAnalyzer opens the Signal Analyzer
app.
signalAnalyzer(sig)
sig)signalAnalyzer( opens the
Signal Analyzer app and imports and plots the signal
sig)sig. If the app is already open, then it plots
sig in the current display. If sig is
already plotted but has changed, then the function call updates the plot.
sig can be a variable in the workspace or a MATLAB expression. sig can be:
A vector or a matrix with independent signals in each column.
A
timetablewith time values specified as durations.A
timeseriesobject.
See Data Types Supported by Signal Analyzer for more details.
By default, the app plots the signal as a function of sample index. If you provide time information, or if the signal has inherent time information, then the app plots the signal as a function of time.
signalAnalyzer(sig1,...,sigN)
sig1,...,sigN)signalAnalyzer( imports
N signal vectors or matrices and plots them in the current
display. The app does not support importing signals with inherent time information
and signals without inherent time information in the same function call.sig1,...,sigN)
signalAnalyzer(___,'SampleRate',fs)
fs)signalAnalyzer(___,'SampleRate',
specifies a sample rate, fs)fs, as a positive scalar expressed in
Hz. The app uses the sample rate to plot one or more signals against time, assuming
a start time of zero. You can specify a sample rate for signals with no inherent
time information.
signalAnalyzer(___,'SampleTime',ts)
ts)signalAnalyzer(___,'SampleTime',
specifies a sample time, ts)ts, as a positive scalar expressed in
seconds. The app uses the sample time to plot one or more signals against time,
assuming a start time of zero. You can specify a sample time for signals with no
inherent time information.
signalAnalyzer(___,'StartTime',st)
st)signalAnalyzer(___,'StartTime',
specifies a signal start time, st)st, as a scalar expressed in
seconds. If you do not specify a sample rate or sample time, then the app assumes a
sample rate of 1 Hz. You can specify a start time for signals with no inherent
time information.
signalAnalyzer(___,'TimeValues',tv)
tv)signalAnalyzer(___,'TimeValues',
specifies a vector, tv)tv, with time values corresponding to the
data points. tv can be a real numeric vector with values
expressed in seconds. tv can also be a duration array. The values in
tv must be unique and cannot be NaN, but
they need not be uniformly spaced. All input signals must have the same length as
tv. You can specify a vector of time values for signals
with no inherent time information.
Filtering and scalogram view do not support nonuniformly sampled signals.
Version History
Introduced in R2016aR2024a: Find and fill missing data
Preprocess signals in the Signal Analyzer app by finding and filling gaps in the data. You can fill missing data with constant values, combinations of neighboring samples, or moving averages. You also can interpolate or apply an autoregressive model.
R2024a: Play audio signals
Play audio signals in the Signal Analyzer app with audio playback controls.
R2023b: Compute and compare more types of spectra
Enjoy more flexibility when computing spectra in Signal Analyzer. Control the window length, the number of discrete Fourier transform points, and the resolution bandwidth.
R2023a: Find and annotate signal peaks
Perform peak measurements for time-domain signals. View signal peak values in the Measurements table and as annotated markers on the display.
R2020a: Label button removed from Signal Analyzer
Signal Analyzer no longer opens Signal Labeler, which is now available as an app. If you want to label signals, open Signal Labeler from the MATLAB Toolstrip or the Command Window.
See Also
Apps
Functions
Topics
- Time-Frequency Gallery
- Using Signal Analyzer App
- Edit Sample Rate and Other Time Information
- Data Types Supported by Signal Analyzer
- Spectrum Computation in Signal Analyzer
- Persistence Spectrum in Signal Analyzer
- Spectrogram Computation in Signal Analyzer
- Scalogram Computation in Signal Analyzer
- Keyboard Shortcuts for Signal Analyzer
- Signal Analyzer Tips and Limitations
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)