Autocorrelation Function of Exponential Sequence
Compute the autocorrelation function of a 28-sample exponential sequence, for .
a = 0.95; N = 28; n = 0:N-1; lags = -(N-1):(N-1); x = a.^n; c = xcorr(x);
Determine analytically to check the correctness of the result. Use a larger sample rate to simulate a continuous situation. The autocorrelation function of the sequence for , with , is
fs = 10; nn = -(N-1):1/fs:(N-1); dd = (1-a.^(2*(N-abs(nn))))/(1-a^2).*a.^abs(nn);
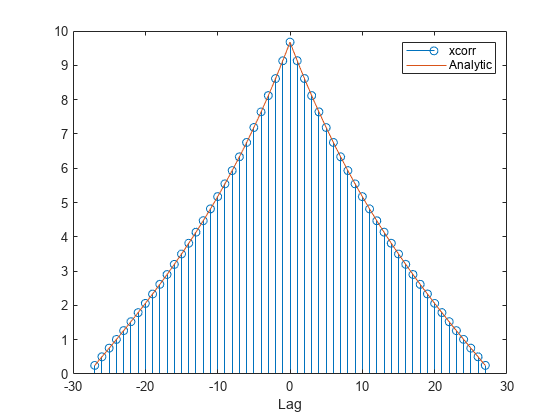
Plot the sequences on the same figure.
stem(lags,c); hold on plot(nn,dd) xlabel('Lag') legend('xcorr','Analytic') hold off
Repeat the calculation, but now find an unbiased estimate of the autocorrelation. Verify that the unbiased estimate is given by .
cu = xcorr(x,'unbiased'); du = dd./(N-abs(nn)); stem(lags,cu); hold on plot(nn,du) xlabel('Lag') legend('xcorr','Analytic') hold off

Repeat the calculation, but now find a biased estimate of the autocorrelation. Verify that the biased estimate is given by .
cb = xcorr(x,'biased'); db = dd/N; stem(lags,cb); hold on plot(nn,db) xlabel('Lag') legend('xcorr','Analytic') hold off

Find an estimate of the autocorrelation whose value at zero lag is unity.
cz = xcorr(x,'coeff'); dz = dd/max(dd); stem(lags,cz); hold on plot(nn,dz) xlabel('Lag') legend('xcorr','Analytic') hold off
