Building a Clutch Lock-Up Model
This example shows how to use Simulink® to model and simulate a rotating clutch system. Although modeling a clutch system is difficult because of topological changes in the system dynamics during lockup, this example shows how enabled subsystem can easily handle such problems. We illustrate how to employ important Simulink modeling concepts in the creation of the clutch simulation. Designers can apply these concepts to many models with strong discontinuities and constraints that may change dynamically.
In the example, you use enabled subsystems to build the clutch model. Two enabled subsystems model the clutch dynamics in either the locked or unlocked position. After running the simulation, a GUI opens. Checking any of the boxes on the GUI produces a plot of any of the selected variables (versus time).
Analysis and Physics
The clutch system in this example consists of two plates that transmit torque between the engine and transmission (see Figure 1). There are two distinct modes of operation:
1) slipping - the two plates have differing angular velocities
2) lockup - the two plates rotate together.
Handling the transition between these two modes presents a modeling challenge. As the system loses a degree of freedom upon lockup, the transmitted torque goes through a step discontinuity. The magnitude of the torque drops from the maximum value supported by the friction capacity to a value that is necessary to keep the two halves of the system spinning at the same rate. The reverse transition, break-apart, is likewise challenging, as the torque transmitted by the clutch plates exceeds the friction capacity.
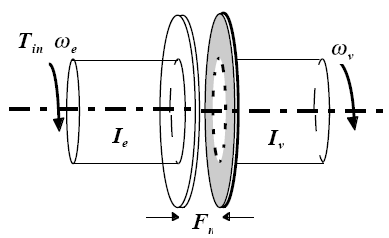
Figure 1: The clutch system, analyzed using a lumped-parameter model
Variables Used
The following variables are used in the analysis and modeling.
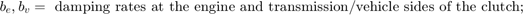
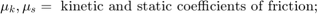
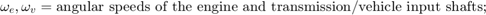
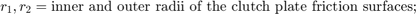
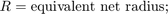
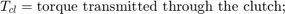
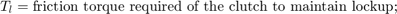
Equation 1
The state equations for the coupled system are derived as follows:
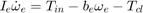
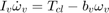
Equation 2
The torque capacity of the clutch is a function of its size, friction characteristics, and the normal force that is applied.
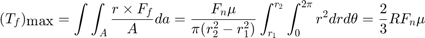
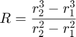
Equation 3
When the clutch is slipping, the model uses the kinetic coefficient of friction and the full capacity is available, in the direction that opposes slip.
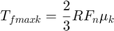
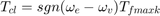
where sgn denotes the sign function.
Equation 4
When the clutch is locked, the angular velocities of the engine and transmission input shafts are the same, and the system torque acts on the combined inertia as a single unit. So, we combine the differential equations (Equation 1) into a single equation for the locked state.
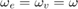
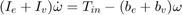
Equation 5
Solving Equation 1 and Equation 4, the torque transmitted by the clutch while locked is:
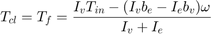
Equation 6
The clutch thus remains locked unless the magnitude of Tf exceeds the static friction capacity, Tfmaxs.
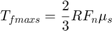
The state diagram in Figure 2 describes the overall behavior of the clutch.
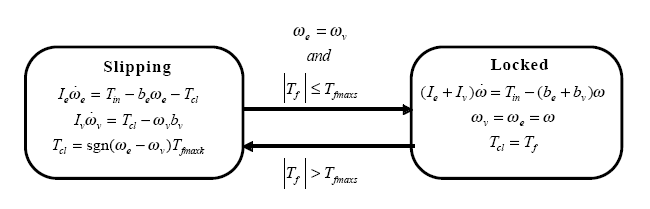
Figure 2: A state diagram describing the friction mode transitions
Modeling
There are two methods for solving this type of problem:
1) Compute the clutch torque transmitted at all times, and employ this value directly in the model.
2) Use two different dynamic models and switch between them at the appropriate times.
Because of its overall capabilities, Simulink can model either method. In this example, we describe a simulation for the second method. In the second method, switching between two dynamic models must be performed with care to ensure that the initialized states of the new model match the state values immediately prior to the switch. But, in either approach, Simulink facilitates accurate simulation due to its ability to recognize the precise moments at which transitions between lockup and slipping occur.
The simulation model for the clutch system uses enabled subsystems, a particularly useful feature in Simulink. The simulation can use one subsystem while the clutch is slipping and the other when it is locked. A diagram of the Simulink model appears in Figure 3.
Opening the Model and Running the Simulation
When the model is open, to run the simulation, click Run.
Note: If you are using MATLAB Help, you can execute code from the example page by selecting the code and pressing F9. You can also Select Code > Right Click > Select "Evaluate Selection".
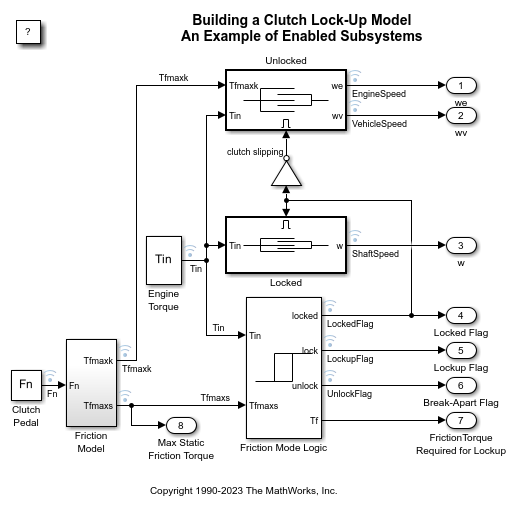
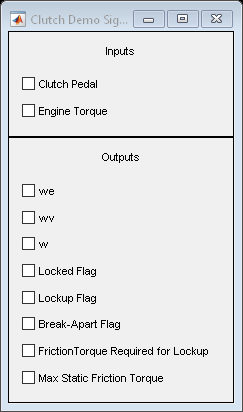
Figure 3: Top level diagram for the clutch model
Note: The model logs relevant data to MATLAB workspace in a structure called
sldemo_clutch_output. For information about signal logging, see Mark Signals for Logging.
The 'Unlocked' Subsystem
Double click on the 'Unlocked' subsystem in the model window to open it. This subsystem models both sides of the clutch, coupled by the friction torque. It is constructed around the integrator blocks which calculate engine and vehicle speeds (see Figure 4). The model uses gain, multiplication, and summation blocks to compute the speed derivatives (acceleration) from the states and the subsystem inputs of engine torque, Tin, and clutch capacity, Tfmaxk.
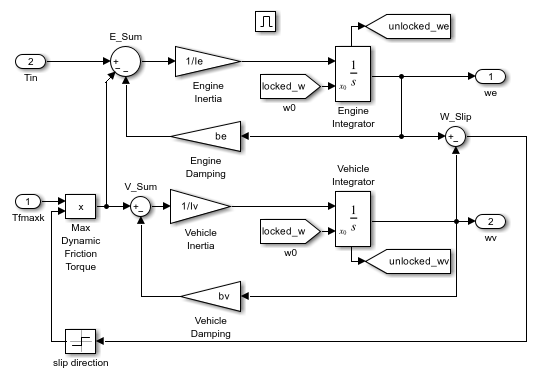
Figure 4: The 'Unlocked' subsystem
Enabled subsystems, such as 'Unlocked', feature several other noteworthy characteristics. The 'Enable' block at the top of the diagram in Figure 4, defines the model as an enabled subsystem. To create an enabled subsystem, we group the blocks together like any other subsystem. We then insert an 'Enable' block from the Simulink Connections library. This means that:
An enable input appears on the subsystem block, identified by the pulse-shaped symbol used on the 'Enable' block itself.
The subsystem executes only when the signal at the enable input is greater than zero.
In this example, the 'Unlocked' subsystem executes only when the supervising system logic determines that it should be enabled.
There is another important consideration when using systems that can be enabled or disabled. When the system is enabled, the simulation must reinitialize the integrators to begin simulating from the correct point. In this case, both sides of the clutch are moving at the same velocity the moment it unlocks. The 'Unlocked' subsystem, which had been dormant, needs to initialize both integrators at that speed in order to keep the system speeds continuous.
The simulation uses 'From' blocks to communicate the state of the locked speed to the initial condition inputs of the two integrators. Each 'From' block represents an invisible connection between itself and a 'Goto' block somewhere else in the system. The 'Goto' blocks connect to the state ports of the integrators so that the model can use these states elsewhere in the system without explicitly drawing in the connecting lines.
The 'Locked' Subsystem
Open the 'Locked' subsystem by double clicking on it in the model window. This is another enabled subsystem in the clutch model (see Figure 5). It uses a single state to represent the engine and vehicle speeds. It computes acceleration as a function of the speed and input torque. As in the 'Unlocked' case, a 'From' block provides the integrator initial conditions and a 'Goto' block broadcasts the state for use elsewhere in the model. While simulating, either the 'Locked' or the 'Unlocked' subsystem is active at all times. Whenever the control changes, the states are neatly handed off between the two.
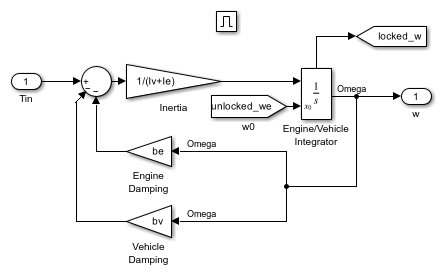
Figure 5: The 'Locked' Subsystem
- The 'Friction Mode Logic' Subsystem
The 'Friction Mode Logic' subsystem (shown in Figure 6) computes the static and kinetic friction (with the appropriate friction coefficient) according to the following formula:
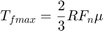
Open the 'Friction Mode Logic' subsystem by double clicking on it in the model window.
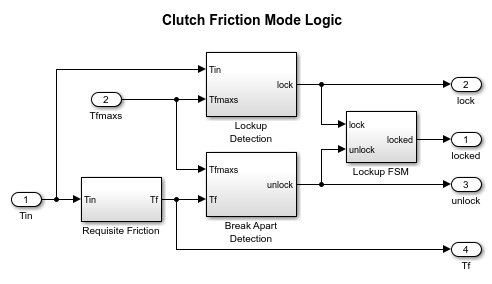
Figure 6: The 'Friction Mode Logic' Subsystem
- Other Components
The remaining blocks calculate the torque required for lockup (Equation 5), and implement the logic described in Figure 2. One key element is located in the 'Lockup Detection' subsystem within the 'Friction Mode Logic' subsystem. This is the 'Simulink Hit Crossing' block which precisely locates the instant at which the clutch slip reaches zero. This places the mode transition at exactly the right moment.
- System Inputs
The system inputs are normal force, Fn, and engine torque, Tin. Each of these is represented by a matrix table in the model workspace. The inputs are plotted in Figure 7. You can visualize various signals by checking the corresponding boxes on the 'Clutch Demo Signals' GUI.
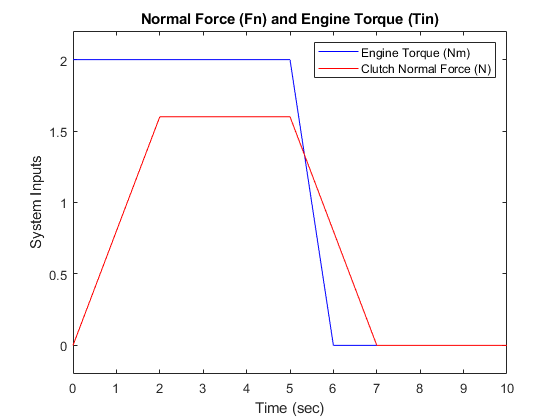
Figure 7: System inputs: normal force and engine torque
Results
The following parameter values are used to show the simulation. These are not meant to represent the physical quantities corresponding to an actual system, but rather to facilitate a meaningful baseline example.
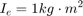
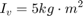
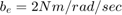
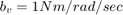
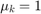

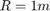
For the inputs shown above, the system velocities behave as shown in Figure 8 below. The simulation begins in the Unlocked mode, with an initial engine speed flare as the vehicle side accelerates its larger inertia. At about t = 4 sec, the velocities come together and remain locked, indicating that the clutch capacity is sufficient to transmit the torque. At t = 5 sec, the engine torque begins to decrease, as does the normal force on the friction plates. Consequently, the onset of slip occurs at about t = 6.25 sec as indicated by the separation of the engine and vehicle speeds.
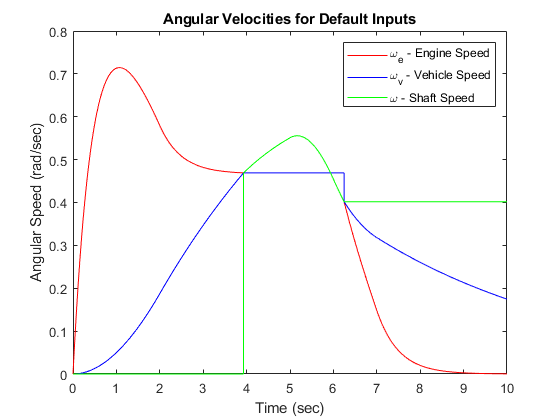
Figure 8: Angular velocities of the engine, vehicle and shaft for default inputs
Notice that the various states remain constant while they are disabled. At the time instants at which transitions take place, the state hand-off is both continuous and smooth. This is a result of supplying each integrator with the appropriate initial conditions to use when the state is enabled.
Closing Model
Close the model. Clear generated data.
Conclusions
This example shows how to use Simulink and its standard block library to model, simulate, and analyze a system with topological discontinuities. This is a powerful example of the 'Hit Crossing' block and how it can be used to capture specific events during a simulation. The Simulink model of this clutch system can serve as a guide when creating models with similar characteristics. You can apply the principles used in this example to any system with topological discontinuities.
