Denoising and Compression
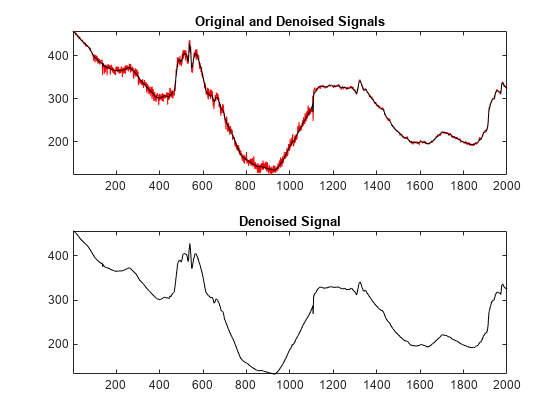
Wavelet and wavelet packet denoising allow you to retain features in your data that are often removed or smoothed out by other denoising techniques. You can compress data by setting perceptually unimportant wavelet and wavelet packet coefficients to zero and reconstructing the data. Noise in a signal is not always uniform in time, so you can apply interval-dependent thresholds to denoise data with nonconstant variance.
Use Wavelet Toolbox™ functions to denoise and obtain compressed signals and images. You can select from many thresholding strategies and explore denoising signals and images by using Wavelet Signal Denoiser.
Categories
- Denoising
Wavelet shrinkage, nonparametric regression, block thresholding, multisignal thresholding
- Compression
Wavelet spatial orientation tree, SPIHT, EZW, WDR, AWDR, matching pursuit