A Simple Finite Volume Solver for Matlab
FVTool: Finite volume toolbox for Matlab
FVTool in:
Python: PyFVTool
Julia: JFVM.jl
FVTool
This is a finite volume (toy) toolbox for chemical/petroleum engineers. Right now, it can solve a transient convection-diffusion equation with variable velocity field/diffusion coefficients. The discretization schemes include:
- central difference diffusion term
- central difference convection term
- upwind convection term
- TVD convection term with various flux limiters
- transient term
- Dirichlet, Neumann, Robin, and periodic boundary conditions
Which equation do you solve?
You can solve the following PDE (or a subset of it):

with the following boundary conditions:
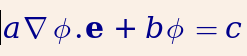
Believe it or not, the above equations describe the majority of the transport phenomena in chemical and petroleum engineering and similar fields.
How to start
Download the package, start matlab, and run
FVToolStartUp
Inspiration
I started writing this tool after playing with FiPy, an amazing python-based finite volume solver. This matlab solver is not a clone, and indeed very limited compared to FiPy. I wrote it to have a very handy tool for testing new ideas (new mathematical models) by solving them in 1D uniform Cartesian grids. Then I extended the code to
- 1D axisymmetric (radial)
- 2D radial (r, theta)
- 2D Cartesian
- 3D Cartesian
- 2D axisymmetric (cylindrical, r, z)
- 3D cylindrical (r, theta, z)
I have overloaded some of the matlab operators to simplify the switch from 1D codes to 2D and 3D.
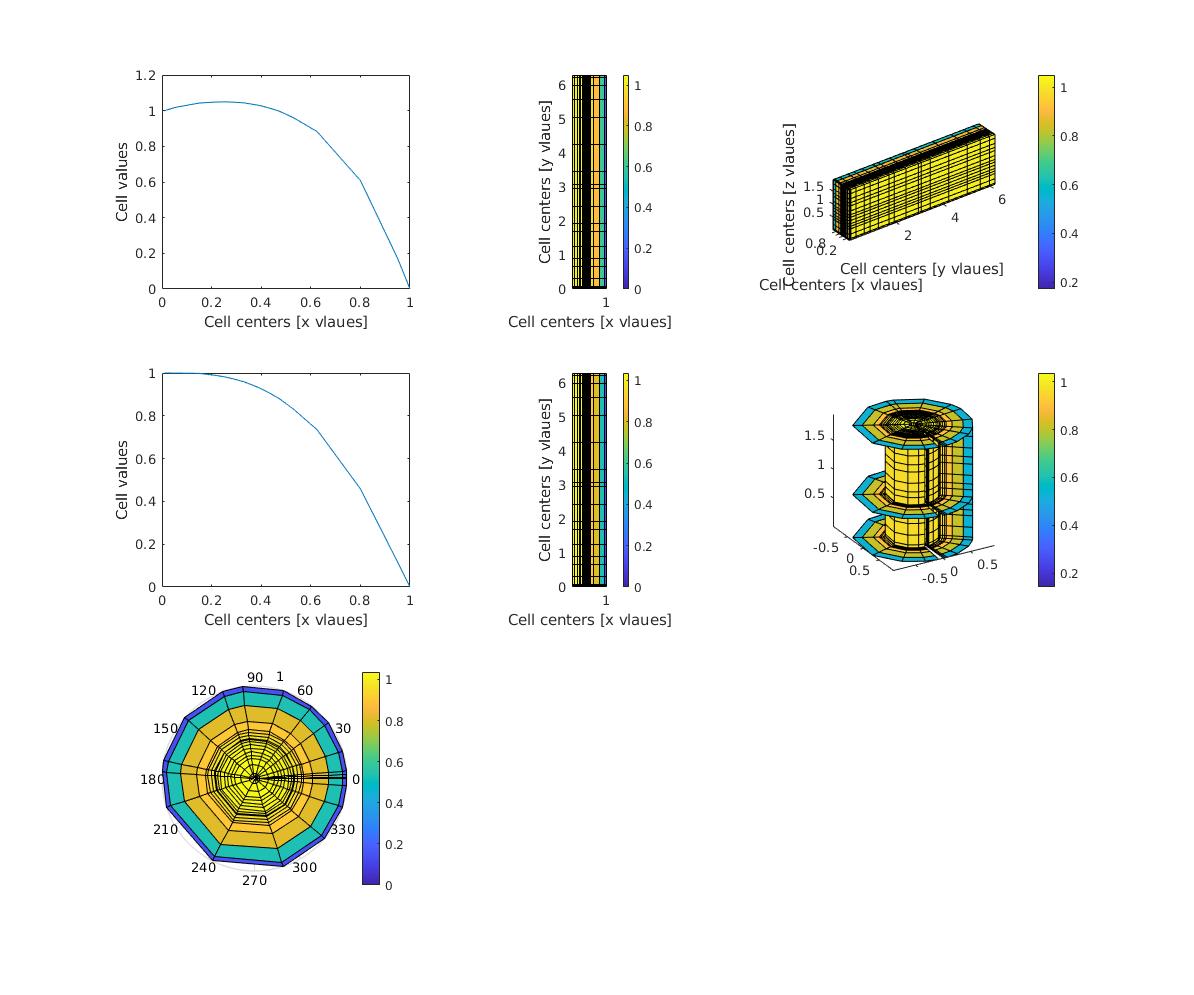
A simple example
You can solve a diffusion equation, i.e., $ \nabla. (-D \nabla \phi) = 0 $ by running the following code in Matlab:
clc
L = 50; % domain length
Nx = 20; % number of cells
m = createMesh1D(Nx, L);
BC = createBC(m); % all Neumann boundary condition structure
BC.left.a(:) = 0; BC.left.b(:)=1; BC.left.c(:)=1; % Dirichlet for the left boundary
BC.right.a(:) = 0; BC.right.b(:)=1; BC.right.c(:)=0; % right boundary
D_val = 1; % value of the diffusion coefficient
D = createCellVariable(m, D_val); % assign the diffusion coefficient to the cells
D_face = harmonicMean(D); % calculate harmonic average of the diffusion coef on the cell faces
Mdiff = diffusionTerm(D_face); % matrix of coefficients for the diffusion term
[Mbc, RHSbc] = boundaryCondition(BC); % matrix of coefficients and RHS vector for the BC
M = Mdiff + Mbc; % matrix of coefficients for the PDE
c = solvePDE(m,M, RHSbc); % send M and RHS to the solver
visualizeCells(c); % visualize the resultschange the third line to m = createMesh2D(Nx,Nx, L,L); or m = createMesh3D(Nx,Nx,Nx, L,L,L); and see the outcome for yourself.
Examples
There are a few simple examples in the Tutorial folder. You can also find a few more advanced examples (water injection into a heterogeneous oil field, two nonlinear PDEs, coupled fully implicit solution) in the Advanced folder.
Documents
Find some preliminary documents here.
But Matlab is not a free software?
You can use the code in octave. The new (object oriented) version of the code works in Octave 4.0 (with the new classdef function).
I've re-written the code in Julia. It works fine, but the visualization on Windows OS has still some issues.
Questions and bug reports
You can ask your questions by creating a new issue here, or by writing a comment in my blog. You can also ask your question in the Matlab file exchange page of this code. I truly appreciate your feedback and/or contribution.
How to cite:
If you have used the package in your work and you find it usefull, please cite it as:
@misc{ali_akbar_eftekhari_2015_32745,
author = {Ali Akbar Eftekhari and Kai Schüller and Ferran Brosa Planella and Martinus Werts and Behzad Hosseinzadeh},
title = {FVTool: a finite volume toolbox for Matlab},
month = oct,
year = 2015,
doi = {10.5281/zenodo.32745},
url = {https://doi.org/10.5281/zenodo.32745}
}
I will also appreciate it if you write me a couple of lines about how you have used it in your research. It encourages me to maintain the code.
Cite As
Eftekhari, A.A. et al. (2015). FVTool: a finite volume toolbox for Matlab. Zenodo. http://doi.org/10.5281/zenodo.32745
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Automotive > Model-Based Calibration Toolbox >
- Mathematics and Optimization > Partial Differential Equation Toolbox > General PDEs > Boundary Conditions >
- Engineering > Petroleum Engineering > Petrophysics >
Tags
Acknowledgements
Inspired by: IAPWS_IF97
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
Boundary
Calculus
Classes/@BoundaryCondition
Classes/@CellVariable
Classes/@CellVector
Classes/@FaceVariable
Classes/@MeshStructure
Discretization
Examples/Advanced
Examples/External/Diffusion1DSpherical_Analytic-vs-FVTool-vs-Fipy
Examples/External/InjectionHClCoreFloodProblem
Examples/External/PhaseChangeEnthalpyMethod
Examples/External/PhaseChangeEnthalpyMethod/Functions
Examples/External/SteadyLidDrivenCavityProblem
Examples/External/SteadyLidDrivenCavityProblem/Functions
Examples/External/SteadyLidDrivenCavityProblem/Testcases
Examples/Tutorial
FieldGeology
MeshGeneration
PhysicalProperties
Physics
Solvers
Tests
Utilities
Visualization
Examples/Validation
Versions that use the GitHub default branch cannot be downloaded
| Version | Published | Release Notes | |
|---|---|---|---|
| 2.1.1.0 | Switched to github repository readme |
|
|
| 2.1.0.0 | Citation information and some clean up |
|
|
| 2.0.0.0 | showdemo function is not available. I will update it later. |
|
|
| 1.4.0.0 | added support for 2D radial (r, theta) and 3D cylindrical (r, thetta, z) |
|
|
| 1.3.0.0 | updated descriptions |
|
|
| 1.2.0.0 | update my weblog address |
|
|
| 1.1.0.0 | add youtube channel link to descriptions |
|
|
| 1.0.0.0 |
|