Vector algebra for arrays of any size, with array expansion enabled
This toolbox was written to complete the incomplete set of vectorial operations provided with MATLAB, and to enhance the features of two of them (DOT and CROSS), by enabling virtual array expansion (AX). AX is enabled in all the binary operations included in this toolbox, and allows you, for instance, to multiply a single vector with an array of vectors, by virtually replicating the vector to match the size of the array.
All the functions in this toolbox can automatically operate on block arrays (arrays of any size containing vectors along one of their dimensions).
MATLAB includes four functions which can apply binary operations on the vectors contained in two block arrays:
+ (generic operator usable to perform vector additions)
- (generic operator usable to perform vector subtractions)
DOT (specific function performing dot products)
CROSS (specific function performing cross products)
They all perform multiple operations, but they cannot perform automatic AX. MATLAB also includes function SUM, which can be used to add together two or more vectors contained in a single matrix or N-D array. For instance, if A is a MN matrix, regarded as a concatenation of N column vectors, these vectors can be added together by using SUM(A, 2), which yields an M1 matrix.
DOT2 and CROSS2, included in this toolbox, enable AX for dot and cross products.
Outer products, orthogonal cross divisions, and generalized cross divisions with AX enabled, can be performed by calling functions OUTER, OCD, and CROSSDIV, included in this toolbox.
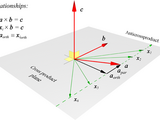
As for cross divisions (CDs), they were not invented until now (see Weisstein, 2008), but I needed them, so I defined and implemented them (de Leva, 2008). They determine one of the infinitely many anticrossproducts of the cross product a b (see screenshot). They were not indispensable, but markedly simplified my equations and my code, and those who appreciate short symbolic equations are likely to love them. Without CDs, in some cases you are forced to write scalar equations, containing negative terms and operations involving various combinations of scalar components. In other cases, you need to write longer vectorial equations. Those equations are not complex, but they are certainly less simple than a CD. For instance, a typo is more likely to occur when you write scalar equations than when you write a CD. See CROSSDIV help for more detailed explanations.
A list of simple vectorial operations is given below. Only the first five are implemented in intrinsic MATLAB functions. The others are implemented in this toolbox. All of them can operate on N-D arrays of vectors. See the respective help texts for further details.
Operation: MATLAB implementation
------------------------------------------------
Repeated addition: SUM
Binary addition: +
Subtraction: -
Dot product: DOT
Cross product: CROSS
Operation: ARRAYLAB implementation
----------------------------------------------------
Euclidean norm: MAGN
Normalization: UNIT
Dot product (AX enabled): DOT2
Cross product (AX enabled): CROSS2
Outer product (AX enabled): OUTER
Orthogonal cross division (AX enabled): OCD
Generalized cross division (AX enabled): CROSSDIV
Projection (AX enabled): PROJECTION
Rejection (AX enabled): REJECTION
A detailed definition of AX is given in the manual of the MULTIPROD toolbox, published on MATLAB Central (file #8773).
The ARRAYLAB toolbox
The functions included in this toolbox comply with the ARRAYLAB philosophy, and are a part of the "ARRAYLAB toolbox" (see the manual of the MULTIPROD toolbox, MATLAB Central, file #8773).
Some of them call MULTIPROD. This function is a powerful generalization for N-D arrays of the MATLAB function MTIMES and the matrix multiplication operator (*).
MULTIPROD has a broad field of potential applications. For instance, it can use large arrays of 33 or 44 transformation matrices to perform, in a single step and with no loops, multiple geometrical transformations (rotations, roto-translations) on arrays of vectors. Thus, it deserves a separate introduction and I published it in a separate package on MATLAB Central (file #8773).
Some other functions of this toolbox call BAXFUN, another function which belongs to the ARRAYLAB toolbox and which is published separately on MATLAB Central (file #23084).
Output testing
The functions testDOT2, testCROSS2, testOUTER, testPROJECTION, testREJECTION, testUNIT, testXDIV, testOCD, stored in a separate folder "Testing", contain the code I used to test the output of the main functions. Since UNIT calls MAGN, testUNIT tests both UNIT and MAGN.
REFERENCES
de Leva P., 2008. Anticrossproducts and cross divisions. Journal of Biomechanics, 8, 1790-1800 (http://dx.doi.org/doi:10.1016/j.jbiomech.2007.09.030)
Weisstein E. W. Vector Division. From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/VectorDivision.html (Retreived on 2008 Dec 4)
Cite As
Paolo de Leva (2024). Vector algebra for arrays of any size, with array expansion enabled (https://www.mathworks.com/matlabcentral/fileexchange/8782-vector-algebra-for-arrays-of-any-size-with-array-expansion-enabled), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Signal Processing > DSP System Toolbox > Statistics and Linear Algebra > Linear Algebra >
- Engineering > Biomedical Engineering > Biomechanics >
Tags
Acknowledgements
Inspired by: Multiple matrix multiplications, with array expansion enabled, Binary array expansion function
Inspired: Normalize N-D Vectors in Single Matrix or N Component Matrices, Dot product of two N-dimensional arrays., Simple acoustic horn design for amplification, Parallel Curves
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
Testing/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.3.0.0 | Version 2.0. Includes two new functions (DOT2, CROSS2). Exploits quicker, more efficient, and more powerful engines. Introduces virtual array expansion, which allows you, for instance, to multiply a single vector by an array of vectors. |
||
| 1.2.0.0 | Removed two unnecessary and not commented files from the "Testing" folder |
||
| 1.1.0.0 | Added references, inserted figure about cross division in toolbox manual |
||
| 1.0.0.0 | Function OUTER now uses the complex conjugate of its first input argument (MATLAB function DOT does the same). Thus, over the complex field, OUTER is not anymore equivalent to a (multiple) matrix multiplication. |