ddensd
Solve delay differential equations (DDEs) of neutral type
Syntax
Description
sol = ddensd(ddefun,dely,delyp,history,tspan)
| y '(t) = f(t, y(t), y(dy1),..., y(dyp), y '(dyp1),..., y '(dypq)) | (1) |
t is the independent variable representing time.
dyi is any of p solution delays.
dypj is any of q derivative delays.
Examples
Neutral DDE with Two Delays
Solve the following neutral DDE, presented by Paul, for 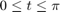 .
.
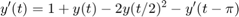
The solution history is 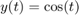 for
for 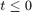 .
.
Create a new program file in the editor. This file will contain a main function and four local functions.
Define the first-order DDE as a local function named ddefun.
function yp = ddefun(t,y,ydel,ypdel) yp = 1 + y - 2*ydel^2 - ypdel; end
Define the solution delay as a local function named dely.
function dy = dely(t,y) dy = t/2; end
Define the derivative delay as a local function named delyp.
function dyp = delyp(t,y) dyp = t-pi; end
Define the solution history as a local function named history.
function y = history(t) y = cos(t); end
Define the interval of integration and solve the DDE using ddensd. Add this code to the main function.
tspan = [0 pi]; sol = ddensd(@ddefun,@dely,@delyp,@history,tspan);
Evaluate the solution at 100 equally spaced points between 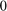 and
and  . Add this code to the main function.
. Add this code to the main function.
tn = linspace(0,pi); yn = deval(sol,tn);
Plot the results. Add this code to the main function.
plot(tn,yn); xlim([0 pi]); ylim([-1.2 1.2]); xlabel('time t'); ylabel('solution y');
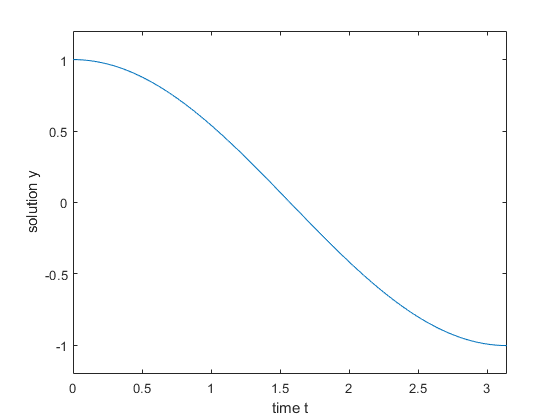
Run your entire program to calculate the solution and display the plot. The file ddex4.m contains the complete code for this example. To see the code in an editor, type edit ddex4 at the command line.
Input Arguments
ddefun — Derivative function
function handle
Derivative function, specified as a function handle whose syntax
is yp = ddefun(t,y,ydel,ypdel). The arguments for ddefun are
described in the table below.
| ddefun Argument | Description |
|---|---|
t | A scalar value representing the current value of time, t. |
y | A vector that represents y(t)
in Equation 1. The size
of this vector is n-by-1, where n is
the number of equations in the system you want to solve. |
ydel | A matrix whose columns, ydel(:,i), represent y(dyi).
The size of this matrix is n-by-p,
where n is the number of equations in the system
you want to solve, and p is the number of y(dy)
terms in Equation 1. |
ypdel | A matrix whose columns, ypdel(:,j) represent y '(dypj).
The size of this matrix is n-by-q,
where n is the number of equations in the system
you want to solve, and q is the number of y '(dyp)
terms in Equation 1. |
yp | The result returned by ddefun. It is an n-by-1 vector
whose elements represent the right side of Equation 1. |
dely — Solution delays
function handle | vector
Solution delays, specified as a function handle, which returns dy1,..., dyp in Equation 1. Alternatively, you can pass constant delays in the form of a vector.
If you specify dely as a function handle,
the syntax must be dy = dely(t,y). The arguments
for this function are described in the table below.
| dely Argument | Description |
|---|---|
t | A scalar value representing the current value of time, t. |
y | A vector that represents y(t)
in Equation 1. The size
of this vector is n-by-1, where n is
the number of equations in the system you want to solve. |
dy | A vector returned by the dely function whose
values are the solution delays, dyi ,
in Equation 1. The size
of this vector is p-by-1, where p is
the number of solution delays in the equation. Each element must be
less than or equal to t. |
If you want to specify constant solution delays having the form dyi = t – τi, then dely must be a vector, where dely(i) = τi.
Each value in this vector must be greater than or equal to zero.
If dy is not present in the problem, set dely to [].
Data Types: function_handle | single | double
delyp — Derivative delays
function handle | vector
Derivative delays, specified as a function handle, which returns dyp1,..., dypq in Equation 1. Alternatively, you can pass constant delays in the form of a vector.
If delyp is a function handle, its syntax
must be dyp = delyp(t,y). The arguments for this
function are described in the table below.
| delyp Argument | Description |
|---|---|
t | A scalar value representing the current value of time, t. |
y | A vector that represents y(t)
in Equation 1. The size
of this vector is n-by-1, where n is
the number of equations in the system you want to solve. |
dyp | A vector returned by the delyp function
whose values are the derivative delays, dypj,
in Equation 1. The size
of this vector must be q-by-1,
where q is the number of solution delays, dypj,
in the equation. Each element of dyp must be less
than t. There is one exception to this restriction:
if you are solving an initial value DDE, the value of dyp can
equal t at t = t0.
For more information, see Initial Value Neutral Delay Differential Equations. |
If you want specify constant derivative delays having the form dypj = t – τj, then delyp must be a vector, where delyp(j) = τj.
Each value in this vector must be greater than zero. An exception
to this restriction occurs when you solve initial value problems for
DDEs of neutral type. In such cases, a value in delyp can
equal zero at t = t0.
See Initial Value Neutral Delay Differential Equations for more information.
If dyp is not present in the problem, set delyp to [].
Data Types: function_handle | single | double
history — Solution history
function handle | column vector | structure (sol, from previous integration) | 1-by-2 cell array
Solution history, specified as a function handle, column vector, sol structure
(from a previous integration), or a cell array. This is the solution
at t ≤ t0.
If the history varies with time, specify the solution history as a function handle whose syntax is
y = history(t). This function returns ann-by-1vector that approximates the solution, y(t), for t <= t0. The length of this vector,n, is the number of equations in the system you want to solve.If y(t) is constant, you can specify
historyas ann-by-1vector of the constant values.If you are calling
ddensdto continue a previous integration to t0, you can specify history as the output,sol, from the previous integration.If you are solving an initial value DDE, specify history as a cell array,
{y0, yp0}. The first element,y0, is a column vector of initial values, y(t0). The second element, yp0, is a column vector whose elements are the initial derivatives, y '(t0). These vectors must be consistent, meaning that they satisfy Equation 1 at t0. See Initial Value Neutral Delay Differential Equations for more information.
Data Types: function_handle | single | double | struct | cell
tspan — Interval of integration
1-by-2 vector
Interval of integration, specified as the vector [t0
tf]. The first element, t0, is the initial
value of t. The second element, tf,
is the final value of t. The value of t0 must
be less than tf.
Data Types: single | double
options — Optional integration parameters
structure returned by ddeset
Output Arguments
sol — Solution
structure
Solution, returned as a structure containing the following fields.
sol.x | Mesh selected by ddensd. |
sol.y | An approximation to y(t) at the mesh points. |
sol.yp | An approximation to y '(t) at the mesh points. |
sol.solver | A character vector identifying the solver, 'ddensd'. |
You can pass sol to the deval function to evaluate the solution
at specific points. For example, y = deval(sol, 0.5*(sol.x(1)
+ sol.x(end))) evaluates the solution at the midpoint of
the interval of integration.
More About
Initial Value Neutral Delay Differential Equations
An initial value DDE has dyi≥t0 and dypj≥t0, for all i and j. At t = t0, all delayed terms reduce to y(dyi) = y(t0) and y '(dypj) = y '(t0):
| y '(t0) = f(t0, y(t0), y(t0),..., y(t0), y '(t0),..., y '(t0)) | (2) |
When you solve initial value neutral DDEs, you must supply y '(t0)
to ddensd. To do this, specify history as
a cell array {Y0,YP0}. Here, Y0 is
the column vector of initial values, y(t0), and YP0 is a column vector of
initial derivatives, y '(t0). These vectors must be consistent, meaning that they
satisfy Equation 2 at t0.
Algorithms
For information about the algorithm used in this solver, see Shampine [2].
References
[1] Paul, C.A.H. “A Test Set of Functional Differential Equations.” Numerical Analysis Reports. No. 243. Manchester, UK: Math Department, University of Manchester, 1994.
[2] Shampine, L.F. “Dissipative Approximations to Neutral DDEs.” Applied Mathematics & Computation. Vol. 203, Number 2, 2008, pp. 641–648.
Version History
Introduced in R2012b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)