sbiofit
Perform nonlinear least-squares regression
Statistics and Machine Learning Toolbox™, Optimization Toolbox™, and Global Optimization Toolbox are recommended for this function.
Syntax
Description
fitResults = sbiofit(sm,grpData,ResponseMap,estiminfo)sm using
nonlinear least-squares regression.
grpData is a groupedData object specifying
the data to fit. ResponseMap defines the mapping between
the model components and response data in grpData.
estimatedInfo is an EstimatedInfo object that
defines the estimated parameters in the model sm.
fitResults is a OptimResults object or
NLINResults object or a vector
of these objects.
sbiofit uses the first available estimation function among the following:
lsqnonlin (Optimization Toolbox), nlinfit (Statistics and Machine Learning Toolbox), or fminsearch.
By default, each group in grpData is fit separately, resulting in
group-specific parameter estimates. If the model contains active doses and
variants, they are applied before the simulation.
fitResults = sbiofit(sm,grpData,ResponseMap,estiminfo,dosing)dosing instead of using the active doses of the model
sm if there is any.
fitResults = sbiofit(sm,grpData,ResponseMap,estiminfo,dosing,functionName)functionName. If
the specified function is unavailable, a warning is issued and the first
available default function is used.
fitResults = sbiofit(sm,grpData,ResponseMap,estiminfo,dosing,functionName,options)options for the
function functionName.
fitResults = sbiofit(sm,grpData,ResponseMap,estiminfo,dosing,functionName,options,variants)variants instead of
using any active variants of the model.
fitResults = sbiofit(_,Name,Value)Name,Value pair
arguments.
[ also returns a vector of SimData objects fitResults,simdata]
= sbiofit(_)simdata using
any of the input arguments in the previous syntaxes.
Note
sbiofitunifiessbionlinfitandsbioparamestimestimation functions. Usesbiofitto perform nonlinear least-squares regression.sbiofitsimulates the model using aSimFunction object, which automatically accelerates simulations by default. Hence it is not necessary to runsbioacceleratebefore you callsbiofit.
Examples
Fit One-Compartment Model to Individual PK Profile
Background
This example shows how to fit an individual's PK profile data to one-compartment model and estimate pharmacokinetic parameters.
Suppose you have drug plasma concentration data from an individual and want to estimate the volume of the central compartment and the clearance. Assume the drug concentration versus the time profile follows the monoexponential decline , where is the drug concentration at time t, is the initial concentration, and is the elimination rate constant that depends on the clearance and volume of the central compartment .
The synthetic data in this example was generated using the following model, parameters, and dose:
One-compartment model with bolus dosing and first-order elimination
Volume of the central compartment (
Central) = 1.70 literClearance parameter (
Cl_Central) = 0.55 liter/hourConstant error model
Bolus dose of 10 mg
Load Data and Visualize
The data is stored as a table with variables Time and Conc that represent the time course of the plasma concentration of an individual after an intravenous bolus administration measured at 13 different time points. The variable units for Time and Conc are hour and milligram/liter, respectively.
load('data15.mat') plot(data.Time,data.Conc,'b+') xlabel('Time (hour)'); ylabel('Drug Concentration (milligram/liter)');

Convert to groupedData Format
Convert the data set to a groupedData object, which is the required data format for the fitting function sbiofit for later use. A groupedData object also lets you set independent variable and group variable names (if they exist). Set the units of the Time and Conc variables. The units are optional and only required for the UnitConversion feature, which automatically converts matching physical quantities to one consistent unit system.
gData = groupedData(data);
gData.Properties.VariableUnits = {'hour','milligram/liter'};
gData.Propertiesans = struct with fields:
Description: ''
UserData: []
DimensionNames: {'Row' 'Variables'}
VariableNames: {'Time' 'Conc'}
VariableDescriptions: {}
VariableUnits: {'hour' 'milligram/liter'}
VariableContinuity: []
RowNames: {}
CustomProperties: [1×1 matlab.tabular.CustomProperties]
GroupVariableName: ''
IndependentVariableName: 'Time'
groupedData automatically set the name of the IndependentVariableName property to the Time variable of the data.
Construct a One-Compartment Model
Use the built-in PK library to construct a one-compartment model with bolus dosing and first-order elimination where the elimination rate depends on the clearance and volume of the central compartment. Use the configset object to turn on unit conversion.
pkmd = PKModelDesign; pkc1 = addCompartment(pkmd,'Central'); pkc1.DosingType = 'Bolus'; pkc1.EliminationType = 'linear-clearance'; pkc1.HasResponseVariable = true; model = construct(pkmd); configset = getconfigset(model); configset.CompileOptions.UnitConversion = true;
For details on creating compartmental PK models using the SimBiology® built-in library, see Create Pharmacokinetic Models.
Define Dosing
Define a single bolus dose of 10 milligram given at time = 0. For details on setting up different dosing schedules, see Doses in SimBiology Models.
dose = sbiodose('dose'); dose.TargetName = 'Drug_Central'; dose.StartTime = 0; dose.Amount = 10; dose.AmountUnits = 'milligram'; dose.TimeUnits = 'hour';
Map Response Data to the Corresponding Model Component
The data contains drug concentration data stored in the Conc variable. This data corresponds to the Drug_Central species in the model. Therefore, map the data to Drug_Central as follows.
responseMap = {'Drug_Central = Conc'};Specify Parameters to Estimate
The parameters to fit in this model are the volume of the central compartment (Central) and the clearance rate (Cl_Central). In this case, specify log-transformation for these biological parameters since they are constrained to be positive. The estimatedInfo object lets you specify parameter transforms, initial values, and parameter bounds if needed.
paramsToEstimate = {'log(Central)','log(Cl_Central)'};
estimatedParams = estimatedInfo(paramsToEstimate,'InitialValue',[1 1],'Bounds',[1 5;0.5 2]);Estimate Parameters
Now that you have defined one-compartment model, data to fit, mapped response data, parameters to estimate, and dosing, use sbiofit to estimate parameters. The default estimation function that sbiofit uses will change depending on which toolboxes are available. To see which function was used during fitting, check the EstimationFunction property of the corresponding results object.
fitConst = sbiofit(model,gData,responseMap,estimatedParams,dose);
Display Estimated Parameters and Plot Results
Notice the parameter estimates were not far off from the true values (1.70 and 0.55) that were used to generate the data. You may also try different error models to see if they could further improve the parameter estimates.
fitConst.ParameterEstimates
ans=2×4 table
Name Estimate StandardError Bounds
______________ ________ _____________ __________
{'Central' } 1.6993 0.034821 1 5
{'Cl_Central'} 0.53358 0.01968 0.5 2
s.Labels.XLabel = 'Time (hour)'; s.Labels.YLabel = 'Concentration (milligram/liter)'; plot(fitConst,'AxesStyle',s);

Use Different Error Models
Try three other supported error models (proportional, combination of constant and proportional error models, and exponential).
fitProp = sbiofit(model,gData,responseMap,estimatedParams,dose,... 'ErrorModel','proportional'); fitExp = sbiofit(model,gData,responseMap,estimatedParams,dose,... 'ErrorModel','exponential'); fitComb = sbiofit(model,gData,responseMap,estimatedParams,dose,... 'ErrorModel','combined');
Use Weights Instead of an Error Model
You can specify weights as a numeric matrix, where the number of columns corresponds to the number of responses. Setting all weights to 1 is equivalent to the constant error model.
weightsNumeric = ones(size(gData.Conc));
fitWeightsNumeric = sbiofit(model,gData,responseMap,estimatedParams,dose,'Weights',weightsNumeric);Alternatively, you can use a function handle that accepts a vector of predicted response values and returns a vector of weights. In this example, use a function handle that is equivalent to the proportional error model.
weightsFunction = @(y) 1./y.^2;
fitWeightsFunction = sbiofit(model,gData,responseMap,estimatedParams,dose,'Weights',weightsFunction);Compare Information Criteria for Model Selection
Compare the loglikelihood, AIC, and BIC values of each model to see which error model best fits the data. A larger likelihood value indicates the corresponding model fits the model better. For AIC and BIC, the smaller values are better.
allResults = [fitConst,fitWeightsNumeric,fitWeightsFunction,fitProp,fitExp,fitComb];
errorModelNames = {'constant error model','equal weights','proportional weights', ...
'proportional error model','exponential error model',...
'combined error model'};
LogLikelihood = [allResults.LogLikelihood]';
AIC = [allResults.AIC]';
BIC = [allResults.BIC]';
t = table(LogLikelihood,AIC,BIC);
t.Properties.RowNames = errorModelNames;
tt=6×3 table
LogLikelihood AIC BIC
_____________ _______ _______
constant error model 3.9866 -3.9732 -2.8433
equal weights 3.9866 -3.9732 -2.8433
proportional weights -3.8472 11.694 12.824
proportional error model -3.8257 11.651 12.781
exponential error model 1.1984 1.6032 2.7331
combined error model 3.9163 -3.8326 -2.7027
Based on the information criteria, the constant error model (or equal weights) fits the data best since it has the largest loglikelihood value and the smallest AIC and BIC.
Display Estimated Parameter Values
Show the estimated parameter values of each model.
Estimated_Central = zeros(6,1); Estimated_Cl_Central = zeros(6,1); t2 = table(Estimated_Central,Estimated_Cl_Central); t2.Properties.RowNames = errorModelNames; for i = 1:height(t2) t2{i,1} = allResults(i).ParameterEstimates.Estimate(1); t2{i,2} = allResults(i).ParameterEstimates.Estimate(2); end t2
t2=6×2 table
Estimated_Central Estimated_Cl_Central
_________________ ____________________
constant error model 1.6993 0.53358
equal weights 1.6993 0.53358
proportional weights 1.9045 0.51734
proportional error model 1.8777 0.51147
exponential error model 1.7872 0.51701
combined error model 1.7008 0.53271
Conclusion
This example showed how to estimate PK parameters, namely the volume of the central compartment and clearance parameter of an individual, by fitting the PK profile data to one-compartment model. You compared the information criteria of each model and estimated parameter values of different error models to see which model best explained the data. Final fitted results suggested both the constant and combined error models provided the closest estimates to the parameter values used to generate the data. However, the constant error model is a better model as indicated by the loglikelihood, AIC, and BIC information criteria.
Fit Two-Compartment Model to PK Profiles of Multiple Individuals
Suppose you have drug plasma concentration data from three individuals that you want
to use to estimate corresponding pharmacokinetic parameters, namely the volume of
central and peripheral compartment (Central,
Peripheral), the clearance rate (Cl_Central),
and intercompartmental clearance (Q12). Assume the drug concentration
versus the time profile follows the biexponential decline , where Ct is the drug
concentration at time t, and a and
b are slopes for corresponding exponential declines.
The synthetic data set contains drug plasma concentration data measured in both central and peripheral compartments. The data was generated using a two-compartment model with an infusion dose and first-order elimination. These parameters were used for each individual.
Central | Peripheral | Q12 | Cl_Central | |
|---|---|---|---|---|
| Individual 1 | 1.90 | 0.68 | 0.24 | 0.57 |
| Individual 2 | 2.10 | 6.05 | 0.36 | 0.95 |
| Individual 3 | 1.70 | 4.21 | 0.46 | 0.95 |
The data is stored as a table with variables ID, Time, CentralConc, and PeripheralConc. It represents the time course of plasma concentrations measured at eight different time points for both central and peripheral compartments after an infusion dose.
load('data10_32R.mat')
Convert the data set to a groupedData object which is the required
data format for the fitting function sbiofit for later use. A
groupedData object also lets you set independent variable and
group variable names (if they exist). Set the units of the ID,
Time, CentralConc, and
PeripheralConc variables. The units are optional and only
required for the UnitConversion feature, which
automatically converts matching physical quantities to one consistent unit
system.
gData = groupedData(data);
gData.Properties.VariableUnits = {'','hour','milligram/liter','milligram/liter'};
gData.Properties
ans =
struct with fields:
Description: ''
UserData: []
DimensionNames: {'Row' 'Variables'}
VariableNames: {'ID' 'Time' 'CentralConc' 'PeripheralConc'}
VariableDescriptions: {}
VariableUnits: {'' 'hour' 'milligram/liter' 'milligram/liter'}
VariableContinuity: []
RowNames: {}
CustomProperties: [1x1 matlab.tabular.CustomProperties]
GroupVariableName: 'ID'
IndependentVariableName: 'Time'
Create a trellis plot that shows the PK profiles of three individuals.
sbiotrellis(gData,'ID','Time',{'CentralConc','PeripheralConc'},... 'Marker','+','LineStyle','none');

Use the built-in PK library to construct a two-compartment model with infusion dosing and first-order elimination where the elimination rate depends on the clearance and volume of the central compartment. Use the configset object to turn on unit conversion.
pkmd = PKModelDesign; pkc1 = addCompartment(pkmd,'Central'); pkc1.DosingType = 'Infusion'; pkc1.EliminationType = 'linear-clearance'; pkc1.HasResponseVariable = true; pkc2 = addCompartment(pkmd,'Peripheral'); model = construct(pkmd); configset = getconfigset(model); configset.CompileOptions.UnitConversion = true;
Assume every individual receives an infusion dose at time = 0, with a total infusion amount of 100 mg at a rate of 50 mg/hour. For details on setting up different dosing strategies, see Doses in SimBiology Models.
dose = sbiodose('dose','TargetName','Drug_Central'); dose.StartTime = 0; dose.Amount = 100; dose.Rate = 50; dose.AmountUnits = 'milligram'; dose.TimeUnits = 'hour'; dose.RateUnits = 'milligram/hour';
The data contains measured plasma concentrations in the central and peripheral compartments. Map these variables to the appropriate model species, which are Drug_Central and Drug_Peripheral.
responseMap = {'Drug_Central = CentralConc','Drug_Peripheral = PeripheralConc'};
The parameters to estimate in this model are the volumes of central and peripheral compartments (Central and Peripheral), intercompartmental clearance Q12, and clearance rate Cl_Central. In this case, specify log-transform for Central and Peripheral since they are constrained to be positive. The estimatedInfo object lets you specify parameter transforms, initial values, and parameter bounds (optional).
paramsToEstimate = {'log(Central)','log(Peripheral)','Q12','Cl_Central'};
estimatedParam = estimatedInfo(paramsToEstimate,'InitialValue',[1 1 1 1]);
Fit the model to all of the data pooled together, that is, estimate one set of parameters for all individuals. The default estimation method that sbiofit uses will change depending on which toolboxes are available. To see which estimation function sbiofit used for the fitting, check the EstimationFunction property of the corresponding results object.
pooledFit = sbiofit(model,gData,responseMap,estimatedParam,dose,'Pooled',true)
pooledFit =
OptimResults with properties:
ExitFlag: 3
Output: [1x1 struct]
GroupName: []
Beta: [4x3 table]
ParameterEstimates: [4x3 table]
J: [24x4x2 double]
COVB: [4x4 double]
CovarianceMatrix: [4x4 double]
R: [24x2 double]
MSE: 6.6220
SSE: 291.3688
Weights: []
LogLikelihood: -111.3904
AIC: 230.7808
BIC: 238.2656
DFE: 44
DependentFiles: {1x3 cell}
Data: [24x4 groupedData]
EstimatedParameterNames: {'Central' 'Peripheral' 'Q12' 'Cl_Central'}
ErrorModelInfo: [1x3 table]
EstimationFunction: 'lsqnonlin'
Plot the fitted results versus the original data. Although three separate plots were generated, the data was fitted using the same set of parameters (that is, all three individuals had the same fitted line).
plot(pooledFit);

Estimate one set of parameters for each individual and see if there is any improvement in the parameter estimates. In this example, since there are three individuals, three sets of parameters are estimated.
unpooledFit = sbiofit(model,gData,responseMap,estimatedParam,dose,'Pooled',false);
Plot the fitted results versus the original data. Each individual was fitted differently (that is, each fitted line is unique to each individual) and each line appeared to fit well to individual data.
plot(unpooledFit);

Display the fitted results of the first individual. The MSE was lower than that of the pooled fit. This is also true for the other two individuals.
unpooledFit(1)
ans =
OptimResults with properties:
ExitFlag: 3
Output: [1x1 struct]
GroupName: 1
Beta: [4x3 table]
ParameterEstimates: [4x3 table]
J: [8x4x2 double]
COVB: [4x4 double]
CovarianceMatrix: [4x4 double]
R: [8x2 double]
MSE: 2.1380
SSE: 25.6559
Weights: []
LogLikelihood: -26.4805
AIC: 60.9610
BIC: 64.0514
DFE: 12
DependentFiles: {1x3 cell}
Data: [8x4 groupedData]
EstimatedParameterNames: {'Central' 'Peripheral' 'Q12' 'Cl_Central'}
ErrorModelInfo: [1x3 table]
EstimationFunction: 'lsqnonlin'
Generate a plot of the residuals over time to compare the pooled and unpooled fit results. The figure indicates unpooled fit residuals are smaller than those of pooled fit as expected. In addition to comparing residuals, other rigorous criteria can be used to compare the fitted results.
t = [gData.Time;gData.Time]; res_pooled = vertcat(pooledFit.R); res_pooled = res_pooled(:); res_unpooled = vertcat(unpooledFit.R); res_unpooled = res_unpooled(:); plot(t,res_pooled,'o','MarkerFaceColor','w','markerEdgeColor','b') hold on plot(t,res_unpooled,'o','MarkerFaceColor','b','markerEdgeColor','b') refl = refline(0,0); % A reference line representing a zero residual title('Residuals versus Time'); xlabel('Time'); ylabel('Residuals'); legend({'Pooled','Unpooled'});

This example showed how to perform pooled and unpooled estimations using sbiofit. As illustrated, the unpooled fit accounts for variations due to the specific subjects in the study, and, in this case, the model fits better to the data. However, the pooled fit returns population-wide parameters. If you want to estimate population-wide parameters while considering individual variations, use sbiofitmixed.
Estimate Category-Specific PK Parameters for Multiple Individuals
This example shows how to estimate category-specific (such as young versus old, male versus female), individual-specific, and population-wide parameters using PK profile data from multiple individuals.
Background
Suppose you have drug plasma concentration data from 30 individuals and want to estimate pharmacokinetic parameters, namely the volumes of central and peripheral compartment, the clearance, and intercompartmental clearance. Assume the drug concentration versus the time profile follows the biexponential decline , where is the drug concentration at time t, and and are slopes for corresponding exponential declines.
Load Data
This synthetic data contains the time course of plasma concentrations of 30 individuals after a bolus dose (100 mg) measured at different times for both central and peripheral compartments. It also contains categorical variables, namely Sex and Age.
clear
load('sd5_302RAgeSex.mat')Convert to groupedData Format
Convert the data set to a groupedData object, which is the required data format for the fitting function sbiofit. A groupedData object also allows you set independent variable and group variable names (if they exist). Set the units of the ID, Time, CentralConc, PeripheralConc, Age, and Sex variables. The units are optional and only required for the UnitConversion feature, which automatically converts matching physical quantities to one consistent unit system.
gData = groupedData(data);
gData.Properties.VariableUnits = {'','hour','milligram/liter','milligram/liter','',''};
gData.Propertiesans = struct with fields:
Description: ''
UserData: []
DimensionNames: {'Row' 'Variables'}
VariableNames: {'ID' 'Time' 'CentralConc' 'PeripheralConc' 'Sex' 'Age'}
VariableDescriptions: {}
VariableUnits: {'' 'hour' 'milligram/liter' 'milligram/liter' '' ''}
VariableContinuity: []
RowNames: {}
CustomProperties: [1x1 matlab.tabular.CustomProperties]
GroupVariableName: 'ID'
IndependentVariableName: 'Time'
The IndependentVariableName and GroupVariableName properties have been automatically set to the Time and ID variables of the data.
Visualize Data
Display the response data for each individual.
t = sbiotrellis(gData,'ID','Time',{'CentralConc','PeripheralConc'},... 'Marker','+','LineStyle','none'); % Resize the figure. t.hFig.Position(:) = [100 100 1280 800];

Set Up a Two-Compartment Model
Use the built-in PK library to construct a two-compartment model with infusion dosing and first-order elimination where the elimination rate depends on the clearance and volume of the central compartment. Use the configset object to turn on unit conversion.
pkmd = PKModelDesign; pkc1 = addCompartment(pkmd,'Central'); pkc1.DosingType = 'Bolus'; pkc1.EliminationType = 'linear-clearance'; pkc1.HasResponseVariable = true; pkc2 = addCompartment(pkmd,'Peripheral'); model = construct(pkmd); configset = getconfigset(model); configset.CompileOptions.UnitConversion = true;
For details on creating compartmental PK models using the SimBiology® built-in library, see Create Pharmacokinetic Models.
Define Dosing
Assume every individual receives a bolus dose of 100 mg at time = 0. For details on setting up different dosing strategies, see Doses in SimBiology Models.
dose = sbiodose('dose','TargetName','Drug_Central'); dose.StartTime = 0; dose.Amount = 100; dose.AmountUnits = 'milligram'; dose.TimeUnits = 'hour';
Map the Response Data to Corresponding Model Components
The data contains measured plasma concentration in the central and peripheral compartments. Map these variables to the appropriate model components, which are Drug_Central and Drug_Peripheral.
responseMap = {'Drug_Central = CentralConc','Drug_Peripheral = PeripheralConc'};Specify Parameters to Estimate
Specify the volumes of central and peripheral compartments Central and Peripheral, intercompartmental clearance Q12, and clearance Cl_Central as parameters to estimate. The estimatedInfo object lets you optionally specify parameter transforms, initial values, and parameter bounds. Since both Central and Peripheral are constrained to be positive, specify a log-transform for each parameter.
paramsToEstimate = {'log(Central)', 'log(Peripheral)', 'Q12', 'Cl_Central'};
estimatedParam = estimatedInfo(paramsToEstimate,'InitialValue',[1 1 1 1]);Estimate Individual-Specific Parameters
Estimate one set of parameters for each individual by setting the 'Pooled' name-value pair argument to false.
unpooledFit = sbiofit(model,gData,responseMap,estimatedParam,dose,'Pooled',false);Display Results
Plot the fitted results versus the original data for each individual (group).
plot(unpooledFit);

For an unpooled fit, sbiofit always returns one results object for each individual.
Examine Parameter Estimates for Category Dependencies
Explore the unpooled estimates to see if there is any category-specific parameters, that is, if some parameters are related to one or more categories. If there are any category dependencies, it might be possible to reduce the number of degrees of freedom by estimating just category-specific values for those parameters.
First extract the ID and category values for each ID
catParamValues = unique(gData(:,{'ID','Sex','Age'}));Add variables to the table containing each parameter's estimate.
allParamValues = vertcat(unpooledFit.ParameterEstimates); catParamValues.Central = allParamValues.Estimate(strcmp(allParamValues.Name, 'Central')); catParamValues.Peripheral = allParamValues.Estimate(strcmp(allParamValues.Name, 'Peripheral')); catParamValues.Q12 = allParamValues.Estimate(strcmp(allParamValues.Name, 'Q12')); catParamValues.Cl_Central = allParamValues.Estimate(strcmp(allParamValues.Name, 'Cl_Central'));
Plot estimates of each parameter for each category. gscatter requires Statistics and Machine Learning Toolbox™. If you do not have it, use other alternative plotting functions such as plot.
h = figure; ylabels = ["Central","Peripheral","Q12","Cl\_Central"]; plotNumber = 1; for i = 1:4 thisParam = estimatedParam(i).Name; % Plot for Sex category subplot(4,2,plotNumber); plotNumber = plotNumber + 1; gscatter(double(catParamValues.Sex), catParamValues.(thisParam), catParamValues.Sex); ax = gca; ax.XTick = []; ylabel(ylabels(i)); legend('Location','bestoutside') % Plot for Age category subplot(4,2,plotNumber); plotNumber = plotNumber + 1; gscatter(double(catParamValues.Age), catParamValues.(thisParam), catParamValues.Age); ax = gca; ax.XTick = []; ylabel(ylabels(i)); legend('Location','bestoutside') end % Resize the figure. h.Position(:) = [100 100 1280 800];

Based on the plot, it seems that young individuals tend to have higher volumes of central and peripheral compartments (Central, Peripheral) than old individuals (that is, the volumes seem to be age-specific). In addition, males tend to have lower clearance rates (Cl_Central) than females but the opposite for the Q12 parameter (that is, the clearance and Q12 seem to be sex-specific).
Estimate Category-Specific Parameters
Use the 'CategoryVariableName' property of the estimatedInfo object to specify which category to use during fitting. Use 'Sex' as the group to fit for the clearance Cl_Central and Q12 parameters. Use 'Age' as the group to fit for the Central and Peripheral parameters.
estimatedParam(1).CategoryVariableName = 'Age'; estimatedParam(2).CategoryVariableName = 'Age'; estimatedParam(3).CategoryVariableName = 'Sex'; estimatedParam(4).CategoryVariableName = 'Sex'; categoryFit = sbiofit(model,gData,responseMap,estimatedParam,dose)
categoryFit =
OptimResults with properties:
ExitFlag: 3
Output: [1x1 struct]
GroupName: []
Beta: [8x5 table]
ParameterEstimates: [120x6 table]
J: [240x8x2 double]
COVB: [8x8 double]
CovarianceMatrix: [8x8 double]
R: [240x2 double]
MSE: 0.4362
SSE: 205.8690
Weights: []
LogLikelihood: -477.9195
AIC: 971.8390
BIC: 1.0052e+03
DFE: 472
DependentFiles: {1x3 cell}
Data: [240x6 groupedData]
EstimatedParameterNames: {'Central' 'Peripheral' 'Q12' 'Cl_Central'}
ErrorModelInfo: [1x3 table]
EstimationFunction: 'lsqnonlin'
When fitting by category (or group), sbiofit always returns one results object, not one for each category level. This is because both male and female individuals are considered to be part of the same optimization using the same error model and error parameters, similarly for the young and old individuals.
Plot Results
Plot the category-specific estimated results.
plot(categoryFit);

For the Cl_Central and Q12 parameters, all males had the same estimates, and similarly for the females. For the Central and Peripheral parameters, all young individuals had the same estimates, and similarly for the old individuals.
Estimate Population-Wide Parameters
To better compare the results, fit the model to all of the data pooled together, that is, estimate one set of parameters for all individuals by setting the 'Pooled' name-value pair argument to true. The warning message tells you that this option will ignore any category-specific information (if they exist).
pooledFit = sbiofit(model,gData,responseMap,estimatedParam,dose,'Pooled',true);Warning: CategoryVariableName property of the estimatedInfo object is ignored when using the 'Pooled' option.
Plot Results
Plot the fitted results versus the original data. Although a separate plot was generated for each individual, the data was fitted using the same set of parameters (that is, all individuals had the same fitted line).
plot(pooledFit);

Compare Residuals
Compare residuals of CentralConc and PeripheralConc responses for each fit.
t = gData.Time;
allResid(:,:,1) = pooledFit.R;
allResid(:,:,2) = categoryFit.R;
allResid(:,:,3) = vertcat(unpooledFit.R);
h = figure;
responseList = {'CentralConc', 'PeripheralConc'};
for i = 1:2
subplot(2,1,i);
oneResid = squeeze(allResid(:,i,:));
plot(t,oneResid,'o');
refline(0,0); % A reference line representing a zero residual
title(sprintf('Residuals (%s)', responseList{i}));
xlabel('Time');
ylabel('Residuals');
legend({'Pooled','Category-Specific','Unpooled'});
end
% Resize the figure.
h.Position(:) = [100 100 1280 800];
As shown in the plot, the unpooled fit produced the best fit to the data as it fit the data to each individual. This was expected since it used the most number of degrees of freedom. The category-fit reduced the number of degrees of freedom by fitting the data to two categories (sex and age). As a result, the residuals were larger than the unpooled fit, but still smaller than the population-fit, which estimated just one set of parameters for all individuals. The category-fit might be a good compromise between the unpooled and pooled fitting provided that any hierarchical model exists within your data.
Estimate Yeast G Protein Model Parameter
This example uses the yeast heterotrimeric G protein model and experimental data reported by [1]. For details about the model, see the Background section in Parameter Scanning, Parameter Estimation, and Sensitivity Analysis in the Yeast Heterotrimeric G Protein Cycle.
Load the G protein model.
sbioloadproject gproteinStore the experimental data containing the time course for the fraction of active G protein.
time = [0 10 30 60 110 210 300 450 600]'; GaFracExpt = [0 0.35 0.4 0.36 0.39 0.33 0.24 0.17 0.2]';
Create a groupedData object based on the experimental data.
tbl = table(time,GaFracExpt); grpData = groupedData(tbl);
Map the appropriate model component to the experimental data. In other words, indicate which species in the model corresponds to which response variable in the data. In this example, map the model parameter GaFrac to the experimental data variable GaFracExpt from grpData.
responseMap = 'GaFrac = GaFracExpt';Use an estimatedInfo object to define the model parameter kGd as a parameter to be estimated.
estimatedParam = estimatedInfo('kGd');Perform the parameter estimation.
fitResult = sbiofit(m1,grpData,responseMap,estimatedParam);
View the estimated parameter value of kGd.
fitResult.ParameterEstimates
ans=1×3 table
Name Estimate StandardError
_______ ________ _____________
{'kGd'} 0.11307 3.4439e-05
Suppose you want to plot the model simulation results using the estimated parameter value. You can either rerun the sbiofit function and specify to return the optional second output argument, which contains simulation results, or use the fitted method to retrieve the results without rerunning sbiofit.
[yfit,paramEstim] = fitted(fitResult);
Plot the simulation results.
sbioplot(yfit);

Estimate Time Lag and Duration of a Dose
This example shows how to estimate the time lag before a bolus dose was administered and the duration of the dose using a one-compartment model.
Load a sample data set.
load lagDurationData.matPlot the data.
plot(data.Time,data.Conc,'x') xlabel('Time (hour)') ylabel('Conc (milligram/liter)')
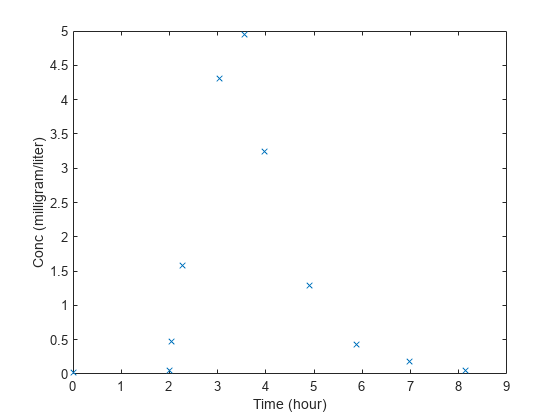
Convert to groupedData.
gData = groupedData(data);
gData.Properties.VariableUnits = {'hour','milligram/liter'};Create a one-compartment model.
pkmd = PKModelDesign; pkc1 = addCompartment(pkmd,'Central'); pkc1.DosingType = 'Bolus'; pkc1.EliminationType = 'linear-clearance'; pkc1.HasResponseVariable = true; model = construct(pkmd); configset = getconfigset(model); configset.CompileOptions.UnitConversion = true;
Add two parameters that represent the time lag and duration of a dose. The lag parameter specifies the time lag before the dose is administered. The duration parameter specifies the length of time it takes to administer a dose.
lagP = addparameter(model,'lagP'); lagP.ValueUnits = 'hour'; durP = addparameter(model,'durP'); durP.ValueUnits = 'hour';
Create a dose object. Set the LagParameterName and DurationParameterName properties of the dose to the names of the lag and duration parameters, respectively. Set the dose amount to 10 milligram which was the amount used to generate the data.
dose = sbiodose('dose'); dose.TargetName = 'Drug_Central'; dose.StartTime = 0; dose.Amount = 10; dose.AmountUnits = 'milligram'; dose.TimeUnits = 'hour'; dose.LagParameterName = 'lagP'; dose.DurationParameterName = 'durP';
Map the model species to the corresponding data.
responseMap = {'Drug_Central = Conc'};Specify the lag and duration parameters as parameters to estimate. Log-transform the parameters. Initialize them to 2 and set the upper bound and lower bound.
paramsToEstimate = {'log(lagP)','log(durP)'};
estimatedParams = estimatedInfo(paramsToEstimate,'InitialValue',2,'Bounds',[1 5]);Perform parameter estimation.
fitResults = sbiofit(model,gData,responseMap,estimatedParams,dose,'fminsearch')fitResults =
OptimResults with properties:
ExitFlag: 1
Output: [1x1 struct]
GroupName: One group
Beta: [2x4 table]
ParameterEstimates: [2x4 table]
J: [11x2 double]
COVB: [2x2 double]
CovarianceMatrix: [2x2 double]
R: [11x1 double]
MSE: 0.0024
SSE: 0.0213
Weights: []
LogLikelihood: 18.7511
AIC: -33.5023
BIC: -32.7065
DFE: 9
DependentFiles: {1x2 cell}
Data: [11x2 groupedData]
EstimatedParameterNames: {'lagP' 'durP'}
ErrorModelInfo: [1x3 table]
EstimationFunction: 'fminsearch'
Display the result.
fitResults.ParameterEstimates
ans=2×4 table
Name Estimate StandardError Bounds
________ ________ _____________ ______
{'lagP'} 1.986 0.0051568 1 5
{'durP'} 1.527 0.012956 1 5
plot(fitResults)
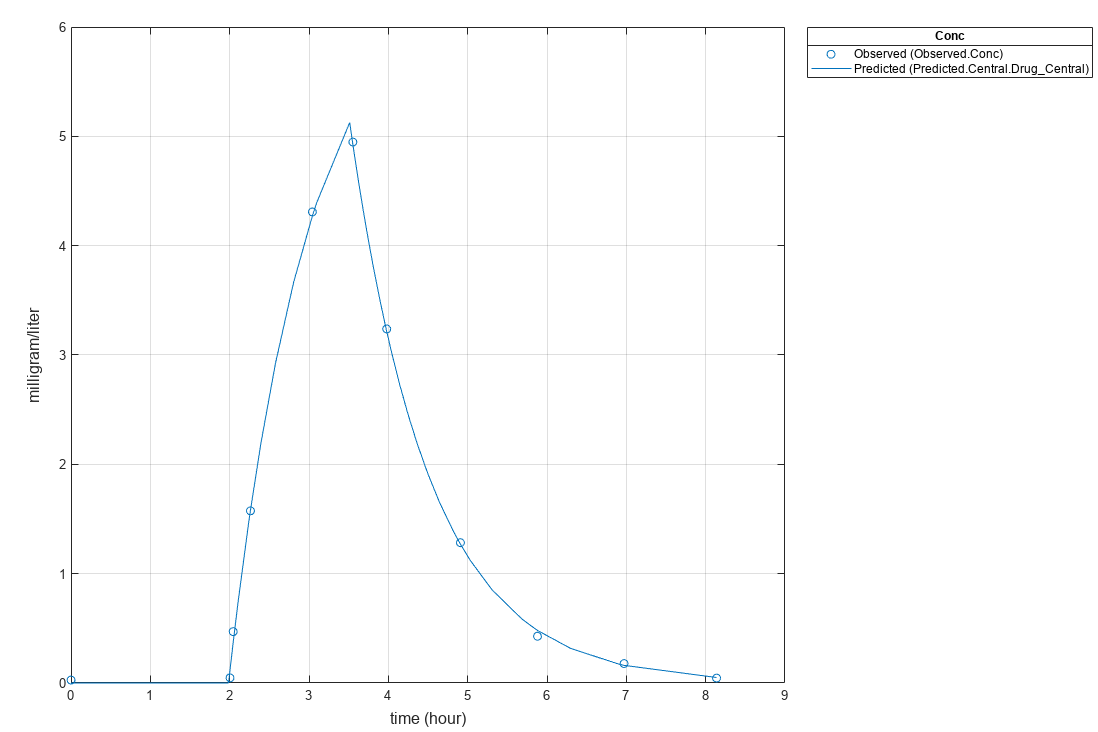
Input Arguments
sm — SimBiology model
SimBiology model object
SimBiology model, specified as a SimBiology model object. The active configset object of the model contains
solver settings for simulation. Any active doses and variants are
applied to the model during simulation unless specified otherwise
using the dosing and variants input
arguments, respectively.
grpData — Data to fit
groupedData object
Data to fit, specified as a groupedData object.
The name of the time variable must be defined in the IndependentVariableName property
of grpData. For instance, if the time variable
name is 'TIME', then specify it as follows.
grpData.Properties.IndependentVariableName = 'TIME'; If the data contains more than one group of measurements, the
grouping variable name must be defined in the GroupVariableName property
of grpData. For example, if the grouping variable
name is 'GROUP', then specify it as follows.
grpData.Properties.GroupVariableName = 'GROUP';Note
sbiofit uses the categorical function
to identify groups. If any group values are converted to the same
value by categorical, then those observations
are treated as belonging to the same group. For instance, if some
observations have no group information (that is, an empty character
vector ''), then categorical converts
empty character vectors to <undefined>, and
these observations are treated as one group.
ResponseMap — Mapping information of model components to grpData
character vector | string | string vector | cell array of character vectors
Mapping information of model components to grpData, specified as a character vector, string, string vector, or cell array of character vectors.
Each character vector or string is an equation-like expression, similar to assignment rules in
SimBiology. It contains the name (or qualified name) of a quantity (species, compartment, or
parameter) or an observable
object in the model sm, followed by the character
'=' and the name of a variable in grpData. For
clarity, white spaces are allowed between names and '='.
For example, if you have the concentration data 'CONC' in
grpData for a species 'Drug_Central', you can
specify it as
follows.
ResponseMap = 'Drug_Central = CONC';To name a species unambiguously, use the qualified name, which includes the name of the compartment. To name a reaction-scoped parameter, use the reaction name to qualify the parameter.
If the model component name or grpData variable name is not a valid
MATLAB® variable name, surround it by square brackets, such as:
ResponseMap = '[Central 1].Drug = [Central 1 Conc]';If a variable name itself contains square brackets, you cannot use it in the expression to define the mapping information.
An error is issued if any (qualified) name matches two components of the same type. However, you can use a (qualified) name that matches two components of different types, and the function first finds the species with the given name, followed by compartments and then parameters.
estiminfo — Estimated parameters
estimatedInfo object | vector of estimatedInfo objects
Estimated parameters, specified as an EstimatedInfo object or
vector of estimatedInfo objects that defines the
estimated parameters in the model sm, and other
optional information such as their initial estimates, transformations, bound
constraints, and categories. Supported transforms are
log, logit, and
probit. For details, see Parameter Transformations.
You can specify bounds for all estimation methods. The lower bound must be less than the upper bound. For details, see Bounds.
When using scattersearch, you must specify
finite transformed bounds for each estimated parameter.
When using fminsearch, nlinfit,
or fminunc with bounds, the objective function
returns Inf if bounds are exceeded. When you turn
on options such as FunValCheck, the optimization
might error if bounds are exceeded during estimation. If using nlinfit,
it might report warnings about the Jacobian being ill-conditioned
or not being able to estimate if the final result is too close to
the bounds.
If you do not specify Pooled name-value pair argument,
sbiofit uses
CategoryVariableName property of
estiminfo to decide if parameters must be estimated
for each individual, group, category, or all individuals as a whole. Use the
Pooled option to override any
CategoryVariableName values. For details about
CategoryVariableName property, see EstimatedInfo object.
Note
sbiofit uses the categorical function
to identify groups or categories. If any group values are converted
to the same value by categorical, then those
observations are treated as belonging to the same group. For instance,
if some observations have no group information (that is, an empty
character vector '' as a group value), then categorical converts empty character
vectors to <undefined>, and these observations
are treated as one group.
dosing — Dosing information
[] | {} | 2-D matrix of dose objects | cell vector of dose objects
Dosing information, specified as an empty array ([] or
{}), 2-D matrix or cell vector of dose objects
(ScheduleDose object or
RepeatDose object).
If you omit the dosing input, the function applies the active doses of the model if there are any.
If you specify the input as empty [] or {}, no doses are applied during simulation, even if the model has active doses.
For a matrix of dose objects, it must have a single row or one row per group in the input data. If it has a single row, the same doses are applied to all groups during simulation. If it has multiple rows, each row is applied to a separate group, in the same order as the groups appear in the input data. Multiple columns are allowed so that you can apply multiple dose objects to each group.
Note
As of R2021b, doses in the columns are no longer required to have the same configuration. If you previously created default (dummy) doses to fill in the columns, these default doses have no effect and indicate no dosing.
For a cell vector of doses, it must have one element or one element per group in the input
data. Each element must be [] or a vector of doses. Each element of the
cell is applied to a separate group, in the same order as the groups appear in the input
data.
In addition to manually constructing dose objects using sbiodose, if the input groupedData object has dosing
information, you can use the createDoses method to construct
doses.
functionName — Estimation function name
character vector | string
Estimation function name, specified as a character vector or string. Choices are as follows.
"fminsearch""nlinfit"(Statistics and Machine Learning Toolbox is required.)"fminunc"(Optimization Toolbox is required.)"fmincon"(Optimization Toolbox is required.)"lsqcurvefit"(Optimization Toolbox is required.)"lsqnonlin"(Optimization Toolbox is required.)"patternsearch"(Global Optimization Toolbox is required.)"ga"(Global Optimization Toolbox is required.)"particleswarm"(Global Optimization Toolbox is required.)
By default, sbiofit uses the first available
estimation function among the following: lsqnonlin (Optimization Toolbox), nlinfit (Statistics and Machine Learning Toolbox), or fminsearch.
The same priority applies to the default local solver choice for scattersearch.
For the summary of supported methods and fitting options, see Supported Methods for Parameter Estimation in SimBiology.
options — Options specific to estimation function
struct | optimoptions object
Options specific to the estimation function, specified as a
struct or optimoptions object.
statsetstruct fornlinfitoptimsetstruct forfminsearchoptimoptionsobject forlsqcurvefit,lsqnonlin,fmincon,fminunc,particleswarm,ga, andpatternsearchstructforscattersearch
See Default Options for Estimation Algorithms for more details and default options associated with each estimation function.
variants — Variants
[] | {} | vector of variant objects
Variants, specified as an empty array ([] or {}) or vector of variant objects.
If you
Omit this input argument, the function applies the active variants of the model if there are any.
Specify this input as empty, no variants are used even if the model has active variants.
Specify this input as a vector of variants, the function applies the specified variants to all simulations, and the model active variants are not used.
Specify this input as a vector of variants and also specify the
Variantsname-value argument, the function applies the variants specified in this input argument before applying the ones specified in the name-value argument.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'ErrorModel','constant','UseParallel',true specifies
a constant error model and to run simulations in parallel during parameter
estimation.
ErrorModel — Error model
'constant' (default) | character vector | string | string vector | cell array of character vector | categorical vector | table
Error models used for estimation, specified as a character vector, string, string vector, cell array of character vectors, categorical vector, or table.
If it is a table, it must contain a single variable that is a column vector of error model
names. The names can be a cell array of character vectors, string vector, or a vector of
categorical variables. If the table has more than one row, then the
RowNames property must match the response variable names specified in
the right hand side of ResponseMap. If the table does not use the
RowNames property, the nth error is associated
with the nth response.
If you specify only one error model, then sbiofit estimates one set of error parameters for all responses.
If you specify multiple error models using a categorical vector, string vector, or cell array
of character vectors, the length of the vector or cell array must match the number of
responses in ResponseMap.
You can specify multiple error models only if you are using these methods: lsqnonlin, lsqcurvefit, fmincon, fminunc, fminsearch, patternsearch, ga, and particleswarm.
Four built-in error models are available. Each model defines the error using a standard mean-zero and unit-variance (Gaussian) variable e, simulation results f, and one or two parameters a and b.
"constant":"proportional":"combined":"exponential":
Note
If you specify an error model, you cannot specify weights except for the constant error model.
If you use a proportional or combined error model during data fitting, avoid specifying data points at times where the solution (simulation result) is zero or the steady state is zero. Otherwise, you can run into division-by-zero problems. It is recommended that you remove those data points from the data set. For details on the error parameter estimation functions, see Maximum Likelihood Estimation.
Weights — Weights used for fitting
[] (default) | matrix | function handle
Weights used for fitting, specified as an empty array [], matrix of real
positive weights where the number of columns corresponds to the number of responses,
or a function handle that accepts a vector of predicted response values and returns
a vector of real positive weights.
If you specify an error model, you cannot use weights except for the constant error model. If
neither the ErrorModel or Weights is specified, by
default, the software uses the constant error model with equal weights.
Variants — Group-specific variants
[] | {} | 2-D matrix of variants | cell vector of variants
Group-specific variants, specified as an empty array
([] or {}), 2-D matrix or cell vector of variant
objects. These variants let you specify parameter values for specific groups during fitting. The
software applies these group-specific variants after active variants or the
variants input argument. If the value is empty ([]
or {}), no group-specific variants are applied.
For a matrix of variant objects, the number of rows must be one or must match the number of groups in the input data. The ith row of variant objects is applied to the simulation of the ith group. The variants are applied in order from the first column to the last. If this matrix has only one row of variants, they are applied to all simulations.
For a cell vector of variant objects, the number of cells must be one or must match the number
of groups in the input data. Each element must be [] or a vector
of variants. If this cell vector has a single cell containing a vector of variants,
they are applied to all simulations. If the cell vector has multiple cells, the
variants in the ith cell are applied to the simulation of the
ith group.
In addition to manually constructing variant objects using
sbiovariant, if the input groupedData
object has variant information, you can use createVariants to construct variants.
Pooled — Fit option flag
false or
0 (default) | true or 1
Fit option flag to fit each individual or pool all individual data,
specified as a numeric or logical 1
(true) or 0
(false).
When true, the software performs fitting for all
individuals or groups simultaneously using the same parameter estimates,
and fitResults is a scalar results object.
When false, the software fits each group or
individual separately using group- or individual-specific parameters,
and fitResults is a vector of results objects with
one result for each group.
Note
Use this option to override any
CategoryVariableName values of
estiminfo.
UseParallel — Flag for parallel simulations
false or
0 (default) | true or 1
Flag to enable parallelization, specified as a numeric or logical 1
(true) or 0
(false). If true and
Parallel Computing Toolbox™ is available, sbiofit supports
several levels of parallelization, but only one level is used at a
time.
For an unpooled fit (Pooled =
false) for multiple groups, each fit is run
in parallel.
For a pooled fit (Pooled =
true), parallelization happens at the solver
level. In other words, solver computations, such as objective
function evaluations, are run in parallel.
For details, see Multiple Parameter Estimations in Parallel.
SensitivityAnalysis — Flag to use parameter sensitivities to determine gradients of the objective function
false or
0 (default) | true or 1
Flag to use parameter sensitivities to determine gradients of the
objective function, specified as a numeric or logical
1 (true) or
0 (false). By default, it is
true for fmincon,
fminunc, lsqnonlin,
lsqcurvefit, and scattersearch
methods. Otherwise, it is false.
If it is true, the software always uses the sundials solver, regardless of what you have selected as the SolverType property in the Configset object.
The software uses the complex-step approximation method to calculate parameter sensitivities. Such calculated sensitivities can be used to determine gradients of the objective function during parameter estimation to improve fitting. The default behavior of sbiofit is to use such sensitivities to determine gradients whenever the algorithm is gradient-based and if the SimBiology model supports sensitivity analysis. For details about the model requirements and sensitivity analysis, see Sensitivity Analysis in SimBiology.
ProgressPlot — Flag to show the progress of parameter estimation
false or
0 (default) | true or 1
Flag to show the progress of parameter estimation, specified as a numeric or logical
1 (true) or
0 (false). If
true, a new figure opens containing plots.
Plots show the log-likelihood, termination criteria, and estimated parameters for each iteration. This option is not supported for nlinfit.
If you are using the Optimization Toolbox functions (fminunc, fmincon, lsqcurvefit, lsqnonlin), the figure also shows the First Order Optimality (Optimization Toolbox) plot.
For an unpooled fit, each line on the plots represents an individual. For a pooled fit, a single line represents all individuals. The line becomes faded when the fit is complete. The plots also keep track of the progress when you run sbiofit (for both pooled and unpooled fits) in parallel using remote clusters. For details, see Progress Plot.
Output Arguments
fitResults — Estimation results
OptimResults object | NLINResults object | vector of results objects
Estimation results, returned as a OptimResults
object or NLINResults object or
a vector of these objects. Both results objects are subclasses of
the LeastSquaresResults object.
If the function uses nlinfit (Statistics and Machine Learning Toolbox),
then fitResults is a NLINResults
object. Otherwise, fitResults is an OptimResults object.
For an unpooled fit, the function fits each group separately using group-specific parameters,
and fitResults is a vector of results objects with one results object
for each group.
For a pooled fit, the function performs fitting for all individuals or groups simultaneously
using the same parameter estimates, and fitResults is a scalar results
object.
When the pooled option is not specified, and CategoryVariableName values of
estimatedInfo objects are all <none>,
fitResults is a single results object. This is the same behavior
as a pooled fit.
When the pooled option is not specified, and CategoryVariableName values of
estimatedInfo objects are all
<GroupVariableName>, fitResults is a
vector of results objects. This is the same behavior as an unpooled fit.
In all other cases, fitResults is a scalar object containing estimated parameter values for different groups or categories specified by CategoryVariableName.
simdata — Simulation results
vector of SimData objects
Simulation results, returned as a vector of SimData objects
representing simulation results for each group or individual.
If the 'Pooled' option is false,
then each simulation uses group-specific parameter values. If true,
then all simulations use the same (population-wide) parameter values.
The states reported in simdata are the states that were included in the
ResponseMap input argument and any other states
listed in the StatesToLog property of the
runtime options (RuntimeOptions) of the SimBiology model
sm.
More About
Maximum Likelihood Estimation
SimBiology® estimates parameters by the method of maximum likelihood. Rather than directly
maximizing the likelihood function, SimBiology constructs an equivalent minimization problem. Whenever possible, the estimation
is formulated as a weighted least squares (WLS) optimization
that minimizes the sum of the squares of weighted residuals. Otherwise, the estimation is
formulated as the minimization of the negative of the logarithm of the likelihood (NLL). The WLS formulation often
converges better than the NLL formulation, and SimBiology can take advantage of specialized WLS algorithms,
such as the Levenberg-Marquardt algorithm implemented in lsqnonlin and
lsqcurvefit. SimBiology uses WLS when there is a single error model that
is constant, proportional, or exponential. SimBiology uses NLL if you have a combined error model or a
multiple-error model, that is, a model having an error model for each response.
sbiofit supports different
optimization methods, and passes in the formulated WLS or
NLL expression to the optimization method that minimizes
it. For simplicity, each expression shown below assumes only one error model and one response.
If there are multiple responses, SimBiology takes the sum of the expressions that correspond to error models of given
responses.
| Expression that is being minimized | |
|---|---|
| Weighted Least Squares (WLS) | For the constant error model, |
| For the proportional error model, | |
| For the exponential error model, | |
| For numeric weights, | |
| Negative Log-likelihood (NLL) | For the combined error model and multiple-error model, |
The variables are defined as follows.
N | Number of experimental observations |
yi | The ith experimental observation |
Predicted value of the ith observation | |
Standard deviation of the ith observation.
| |
The weight of the ith predicted value | |
When you use numeric weights or the weight function, the weights are assumed to be inversely proportional to the variance of the error, that is, where a is the constant error parameter. If you use weights, you cannot specify an error model except the constant error model.
Various optimization methods have different requirements on the function that is being minimized. For some methods, the estimation of model parameters is performed independently of the estimation of the error model parameters. The following table summarizes the error models and any separate formulas used for the estimation of error model parameters, where a and b are error model parameters and e is the standard mean-zero and unit-variance (Gaussian) variable.
| Error Model | Error Parameter Estimation Function |
|---|---|
'constant': | |
'exponential': | |
'proportional': | |
'combined': | Error parameters are included in the minimization. |
| Weights |
Note
nlinfit only support single error models, not multiple-error models, that is, response-specific error models. For a combined error model, it uses an iterative WLS algorithm. For other error models, it uses the WLS algorithm as described previously. For details, see nlinfit (Statistics and Machine Learning Toolbox).
Default Options for Estimation Algorithms
The following table summarizes the default options for various estimation functions.
| Function | Default Options | ||||||
|---|---|---|---|---|---|---|---|
nlinfit (Statistics and Machine Learning Toolbox) |
| ||||||
fmincon (Optimization Toolbox) |
| ||||||
fminunc (Optimization Toolbox) |
| ||||||
fminsearch |
| ||||||
lsqcurvefit (Optimization Toolbox), lsqnonlin (Optimization Toolbox) | Requires Optimization Toolbox.
| ||||||
patternsearch (Global Optimization Toolbox) | Requires Global Optimization Toolbox.
| ||||||
ga (Global Optimization Toolbox) | Requires Global Optimization Toolbox.
| ||||||
particleswarm (Global Optimization Toolbox) | Requires Global Optimization Toolbox.
| ||||||
scattersearch | See Scatter Search Algorithm. |
Scatter Search Algorithm
The scattersearch method implements a global optimization
algorithm [2] that addresses some challenges of parameter estimation in dynamic models, such as
convergence to local minima.
The algorithm selects a subset of points from an initial pool of points. In that subset, some points are the best in quality (that is, lowest function value) and some are randomly selected. The algorithm iteratively evaluates the points and explores different directions around various solutions to find better solutions. During this iteration step, the algorithm replaces any old solution with a new one of better quality. Iterations proceed until any stopping criteria are met. It then runs a local solver on the best point.
Initialization
To start the scatter search, the algorithm first decides the
total number of points needed (NumInitialPoints).
By default, the total is 10*N,
where N is the number of estimated parameters.
It selects NumInitialPoints points (rows) from InitialPointMatrix.
If InitialPointMatrix does not have enough points,
the algorithm calls the function defined in CreationFcn to
generate the additional points needed. By default, Latin hypercube
sampling is used to generate these additional points. The algorithm
then selects a subset of NumTrialPoints points
from NumInitialPoints points. A fraction (FractionInitialBest)
of the subset contains the best points in terms of quality. The remaining
points in the subset are randomly selected.
Iteration Steps
The algorithm iterates on the points in the subset as follows:
Define hyper-rectangles around each pair of points by using the relative qualities (that is, function values) of these points as a measure of bias to create these rectangles.
Evaluate a new solution inside each rectangle. If the new solution outperforms the original solution, replace the original with the new one.
Apply the go-beyond strategy to the improved solutions and exploit promising directions to find better solutions.
Run a local search at every
LocalSearchIntervaliteration. Use theLocalSelectBestProbabilityprobability to select the best point as the starting point for a local search. By default, the decision is random, giving an equal chance to select the best point or a random point from the trial points. If the new solution outperforms the old solution, replace the old one with the new one.Replace any stalled point that does not produce any new outperforming solution after
MaxStallTimeseconds with another point from the initial set.Evaluate stopping criteria. Stop iterating if any criteria are met.
The algorithm then runs a local solver on the best point seen.
Stopping Criteria
The algorithm iterates until it reaches a stopping criterion.
| Stopping Option | Stopping Test |
|---|---|
FunctionTolerance and MaxStallIterations | Relative change in best objective function value over
the last |
MaxIterations | Number of iterations reaches |
OutputFcn |
|
ObjectiveLimit | Best objective function value at an iteration is less
than or equal to |
MaxStallTime | Best objective function value did not change in the last |
MaxTime | Function run time exceeds |
You create the options for the algorithm using a struct.
| Option | Description |
|---|---|
CreationFcn | Handle to the function that creates additional points
needed for the algorithm. Default is the character vector The function signature
is: |
Display | Level of display returned to the command line.
|
FractionInitialBest | Numeric scalar from |
FunctionTolerance | Numeric scalar from |
InitialPointMatrix | Initial (or partial) set of points. M-by-N real finite matrix, where M is the number of points and N is the number of estimated parameters. If M
If
M
Default is the initial transformed values of
estimated parameters stored in the
|
LocalOptions | Options for the local solver. It can be a
|
LocalSearchInterval | Positive integer. Default is |
LocalSelectBestProbability | Numeric scalar from |
LocalSolver | Character vector or string specifying the name of a local solver. Supported methods are
Default local solver is selected with the following priority:
|
MaxIterations | Positive integer. Default is the character vector |
MaxStallIterations | Positive integer. Default is |
MaxStallTime | Positive scalar. Default is |
MaxTime | Positive scalar. Default is |
NumInitialPoints | Positive integer that is |
NumTrialPoints | Positive integer that is |
ObjectiveLimit | Scalar. Default is |
OutputFcn | Function handle or cell array of function handles. Output
functions can read iterative data and stop the solver. Default is Output
function signature is
|
TrialStallLimit | Positive integer, with default value of |
UseParallel | Logical flag to compute objective function in parallel.
Default is |
XTolerance | Numeric scalar from To
get a report of every potential local minimum, set |
Multiple Parameter Estimations in Parallel
There are two ways to use parallel computing for parameter estimation.
'UseParallel' to trueTo enable parallelization for sbiofit, set the name-value pair
'UseParallel' to true. The function
supports several levels of parallelization, but only one level is used at a
time.
For an unpooled fit for multiple groups (or individuals), each group runs in parallel.
For a pooled fit with multiple groups using a solver that has the parallel option, parallelization happens at the solver level. That is,
sbiofitsets the parallel option of the corresponding estimation method (solver) totrue, and the objective function evaluations are performed in parallel. For instance, for a gradient-based method (such aslsqnonlin), the gradients might be computed in parallel. If the solver is not already executing in parallel, then simulations (of different groups) are run in parallel.If you have a single group and are using a solver that does not have the parallel option, setting
UseParallel=truewill run nothing in parallel but still run simulations serially on workers. Thus, It might not be beneficial to enable parallelization because of the overhead time needed by the workers. It might be faster to run without parallelization instead.
parfeval or parforYou can also call sbiofit inside a parfor loop or
use a parfeval inside a for-loop to
perform multiple parameter estimations in parallel. It is recommended that you
use parfeval because these parallel estimations run
asynchronously. If one fit produces an error, it does not affect the other
fits.
If you are trying to find a global minimum, you can use global solvers, such as particleswarm (Global Optimization Toolbox) or ga (Global Optimization Toolbox) (Global Optimization Toolbox is required). However, if you want to define the initial
conditions and run the fits in parallel, see the following example that shows
how to use both parfor and
parfeval.
Model and Data Setup
Load the G protein model.
sbioloadproject gproteinStore the experimental data containing the time course for the fraction of active G protein [1].
time = [0 10 30 60 110 210 300 450 600]'; GaFracExpt = [0 0.35 0.4 0.36 0.39 0.33 0.24 0.17 0.2]';
Create a groupedData object based
on the experimental data.
tbl = table(time,GaFracExpt); grpData = groupedData(tbl);
Map the appropriate model element to the experimental data.
responseMap = 'GaFrac = GaFracExpt';Specify the parameter to estimate.
paramToEstimate = {'kGd'};Generate initial parameter values for kGd.
rng('default');
iniVal = abs(normrnd(0.01,1,10,1));
fitResultPar = [];Parallel Pool Setup
Start a parallel pool using the local profile.
poolObj = parpool('local');Starting parallel pool (parpool) using the 'Processes' profile ... Connected to parallel pool with 4 workers.
Using parfeval (Recommended)
First, define a function handle that uses the local function sbiofitpar for
estimation. Make sure the function sbiofitpar is
defined at the end of the script.
optimfun = @(x) sbiofitpar(m1,grpData,responseMap,x);
Perform multiple parameter estimations in parallel via parfeval using
different initial parameter values.
for i=1:length(iniVal) f(i) = parfeval(optimfun,1,iniVal(i)); end fitResultPar = fetchOutputs(f);
Summarize the results for each run.
allParValues = vertcat(fitResultPar.ParameterEstimates); allParValues.LogLikelihood = [fitResultPar.LogLikelihood]'; allParValues.RunNumber = (1:length(iniVal))'; allParValues.Name = categorical(allParValues.Name); allParValues.InitialValue = iniVal; % Rearrange the columns. allParValues = allParValues(:,[5 1 6 2 3 4]); % Sort rows by LogLikelihood. sortrows(allParValues,'LogLikelihood')
ans=10×6 table
RunNumber Name InitialValue Estimate StandardError LogLikelihood
_________ ____ ____________ ________ _____________ _____________
9 kGd 3.5884 3.022 0.127 -1.2843
10 kGd 2.7794 2.779 0.029701 -1.2319
3 kGd 2.2488 2.2488 0.096013 -1.0786
2 kGd 1.8439 1.844 0.28825 -0.90104
6 kGd 1.2977 1.2977 0.011344 -0.48209
4 kGd 0.87217 0.65951 0.003583 0.9279
1 kGd 0.54767 0.54776 0.0020424 1.5323
7 kGd 0.42359 0.42363 0.0024555 2.6097
8 kGd 0.35262 0.35291 0.00065289 3.6098
5 kGd 0.32877 0.32877 0.00042474 4.0604
Define the local function sbiofitpar that
performs parameter estimation using sbiofit.
function fitresult = sbiofitpar(model,grpData,responseMap,initialValue) estimatedParam = estimatedInfo('kGd'); estimatedParam.InitialValue = initialValue; fitresult = sbiofit(model,grpData,responseMap,estimatedParam); end
Using parfor
Alternatively, you can perform multiple parameter estimations
in parallel via the parfor loop.
parfor i=1:length(iniVal) estimatedParam = estimatedInfo(paramToEstimate,'InitialValue',iniVal(i)); fitResultTemp = sbiofit(m1,grpData,responseMap,estimatedParam); fitResultPar = [fitResultPar;fitResultTemp]; end
Close the parallel pool.
delete(poolObj);
Parallel pool using the 'Processes' profile is shutting down.
Parameter Estimation with Hybrid Solvers
sbiofit supports global optimization methods, namely
ga (Global Optimization Toolbox) and particleswarm (Global Optimization Toolbox) (Global Optimization Toolbox required). To improve optimization results, these methods lets you run
a hybrid function after the global solver stops. The hybrid function uses the final
point returned by the global solver as its initial point. Supported hybrid functions
are:
fminunc(Optimization Toolbox)fmincon(Optimization Toolbox)patternsearch(Global Optimization Toolbox)
Make sure that your hybrid function accepts your problem constraints.
That is, if your parameters are bounded, use an appropriate function
(such as fmincon or patternsearch)
for a constrained optimization. If not bounded, use fminunc, fminsearch,
or patternsearch. Otherwise, sbiofit throws
an error.
For an illustrated example, see Perform Hybrid Optimization Using sbiofit.
References
[1] Yi, T-M., Kitano, H., and Simon, M. (2003). A quantitative characterization of the yeast heterotrimeric G protein cycle. PNAS. 100, 10764–10769.
[2] Gábor, A., and Banga, J.R. (2015). Robust and efficient parameter estimation in dynamic models of biological systems. BMC Systems Biology. 9:74.
Extended Capabilities
Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.
To run in parallel, set 'UseParallel' to true.
For more information, see the 'UseParallel' name-value pair argument.
Version History
Introduced in R2014a
See Also
EstimatedInfo object | groupedData object | LeastSquaresResults object | NLINResults object | OptimResults object | sbiofitmixed | nlinfit (Statistics and Machine Learning Toolbox) | fmincon (Optimization Toolbox) | fminunc (Optimization Toolbox) | fminsearch | lsqcurvefit (Optimization Toolbox) | lsqnonlin (Optimization Toolbox) | patternsearch (Global Optimization Toolbox) | ga (Global Optimization Toolbox) | particleswarm (Global Optimization Toolbox)
Topics
- Parameter Scanning, Parameter Estimation, and Sensitivity Analysis in the Yeast Heterotrimeric G Protein Cycle
- What is Nonlinear Regression?
- Fitting Options in SimBiology
- Parameter Transformations
- Maximum Likelihood Estimation
- Fitting Workflow
- Supported Methods for Parameter Estimation in SimBiology
- Sensitivity Analysis in SimBiology
- Progress Plot
- Supported Files and Data Types
- Create Data File with SimBiology Definitions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)